割り算の等分除と包含除の意味と違いの教え方とは？

算数・数学の基礎となる四則計算は小学校で全て習いますが、四則計算の中でも1番難しいのが割り算です。
「足し算ってどういう意味？」「引き算ってどういう意味？」「掛け算ってどう言う意味？」と聞くと、例を使って説明してくれたり、直接それぞれの計算の概念を説明してくれたりするお子さんがほとんどではないでしょうか。
ただ、四則計算の1つである割り算の意味についてはは答えてくれるお子さんが少なくなります。
今回の記事では、割り算の2つの意味、等分除と包含除^[1]読み方はそれぞれ「とうぶんじょ」、「ほうがんじょ」です。について書いてみたいと思います。

割り算の等分除の意味と教え方のコツ

等分除という言葉は聞いたことがありますか？
あまり耳にしない言葉かもしれません。
小学校で考え方は教わっても、等分除という言葉が出てくるということはないと思います。

等分除はその名の通り等分にするという考え方です。
例題を使って説明します。

この問題を解くのはそんなに難しくありませんよね。
すぐに$$6\div 2=3$$という式を書き、問題を解くことができると思います。
それでは、この問題で立てた割り算の式\(6\div 2=3\)がどういうことを意味するのかを図で考えてみましょう。

りんごが6つあるので、まずはりんごを6つ書きます。
こんな感じです。

次に、これらのりんごを2人で分けるので2つのグループに分けます。

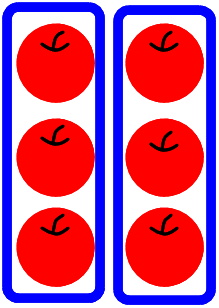
りんごを3つずつ2つのグループに分けることができました。
こんな感じで割る数と同じ数のグループに分けることを等分除といいます。
今回の場合だと2等分にしたという感じです。^[2] … Continue reading

もう1つ等分除の例を挙げてみます。

先ほどの問題ではりんごを2人で分けたのが、今回の例題では3人で分けることになりました。
式を立てると\(6\div 3\)になります。
この割り算の式は「割る数が3」なので「割られる数6」を3等分することを意味します。
そして1グループの個数が商^[3]割り算の答えのことです。となります。

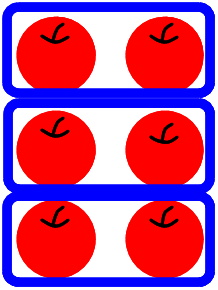
イメージできたでしょうか。
こんな感じで図で考えると分かりやすいと思います。
イメージが作れるまではきちんと絵図を描いていくのがおすすめです。
それでは次に包含除をみていきたいと思います。

割り算の包含除の意味と教え方とコツ

包含除という言葉そのものを聞いたことがないという方も多いのではないでしょうか。
包含除というのは、割る数をいくつ含むのかという考え方のことです。
言葉で言っても分かりにくいので、例題を使って考えていきましょう。

りんごをお皿に2つずつのせていくという問題です。
それでは6つのりんごを2つずつお皿にのせてみましょう。

こんな感じになりました。
りんごが2つのったお皿が3つできました。
このように、「割られる数6」の中に「割る数2」のかたまりがいくつあるのかというのが包含除の考え方になります。
りんご2つのかたまりが、いくつ作れるのか
りんご2つのかたまりが、いくつ入っているのか
という感じでとらえることができるといいですね。^[4]りんごを2つに分けた時の個数がお皿の枚数だと考えると等分除と考えることもできます。

もう1問例題でみてみましょう。

今回の問題では、お皿に3つずつのせることになりました。
式を立ててみると、\(6\div 3\)となります。

\(6\div 3\)の意味を考えてみると、「割る数3」が「割られる数6」の中にいくつあるのかが求められます。
つまり、6個のりんごでりんご3個のかたまりがいくつできるのか、ということが分かります。

計算してみると、\(6\div3=2\)となるので、6の中に3が2つあるということが分かりました。
絵図にするとこんな感じです。

3のかたまりが、2つあるイメージができるといいと思いますよ。
こんな感じで包含除のイメージもできると、割り算の理解が深まるのではないでしょうか。

割り算に等分除と包含除がある理由を考えてみた

割り算には等分除と包含除という意味がなぜあるのかということについて考えてみたいと思います。

それでは解いてみましょう。
\(12\div 2=6\)
となります。

この時に、答えが6であることを求めた際に頭の中で考えたことは、
\(2\times 1=2\)
\(2\times 2=4\)
･･･

と、かけ算九九を思い浮かべると思います。
\(2\times 4=8\)
\(2\times 5=10\)
\(2\times 6=12\)

そして、割られる数の12と掛け算の答えの部分が一致したとき、割り算の答えが求められることになります。

こうやってみてみると不思議ですよね。
割り算とはいいながら、結局していることは掛け算なんですよね。

結局のところ割り算って何をしているんだろう？

割り算を解くときに割り算を使って考えるというのは、難しいです。
掛け算を使わずにとなると、解けそうにありません。
実際に割り算を解くときに考えていることは掛け算ですし。
つまり、ちょっと見方を変えると割り算は掛け算の逆バージョンと言えそうです。

掛け算の意味から割り算の意味を考えてみる

ここで掛け算の意味を復習みると、掛け算は

「1つ分の数」×「いくつ分」=「積(掛け算の答え)」もしくは、「いくつ分」×「1つ分の数」=「積(掛け算の答え)」でした。

このことから、割り算を掛け算の逆だと考えると、2種類の式が立つことが分かります。

「1つ分の数」=「積(掛け算の答え)」÷「いくつ分」
「いくつ分」＝「積」÷「1つ分の数」
この2つの式が立つことになります。

掛け算の式をもとに割り算の式を作ってみると2種類の式が出来ました。

まとめ

今回の記事は割り算の等分除や包含除の意味についてでした。
割り算がどんなことをしているのかが分かればOKです。
等分除とは･･･、包含除とは･･･
なんてことが分からなくても問題ありません。
捉え方次第でどちらにもみえてしまうものです。

割り算で何をしているのかイメージできすることが大切です。

【関連記事はこちら】
・算数の割り算の等分除を使った余りの意味の考え方

・算数の割り算の包含除を使った余りの意味の考え方

・割り算の文章問題で等分除の意味と教え方のコツを説明！

・割り算の文章問題が解けない！包含除の意味から考える教え方って？

・等分除を整数範囲から分数や小数にまで拡張して考えてみよう

・割り算ってなぜ難しいの？