流水算は中学受験でよく出題される特殊算の1つです。
意味も分からず数式を暗記していくとなんのことかよく分からなくなってしまう単元になります。
今回の記事では、流水算の基礎を理解して、解けるようになることを目指します。
流水算が苦手をなくす解き方&教え方のコツは意外と簡単!
ポイント①流水算特有の用語や小学生が聞き慣れない言葉を理解しよう
流水算では普段聞き慣れない用語や聞いたことはあってもはっきりと分からない言葉があります。
まず流水算を解けるようにするためには言葉の意味をしっかり分かってもらうことが一歩目となります。
それでは1つずつみていきましょう。
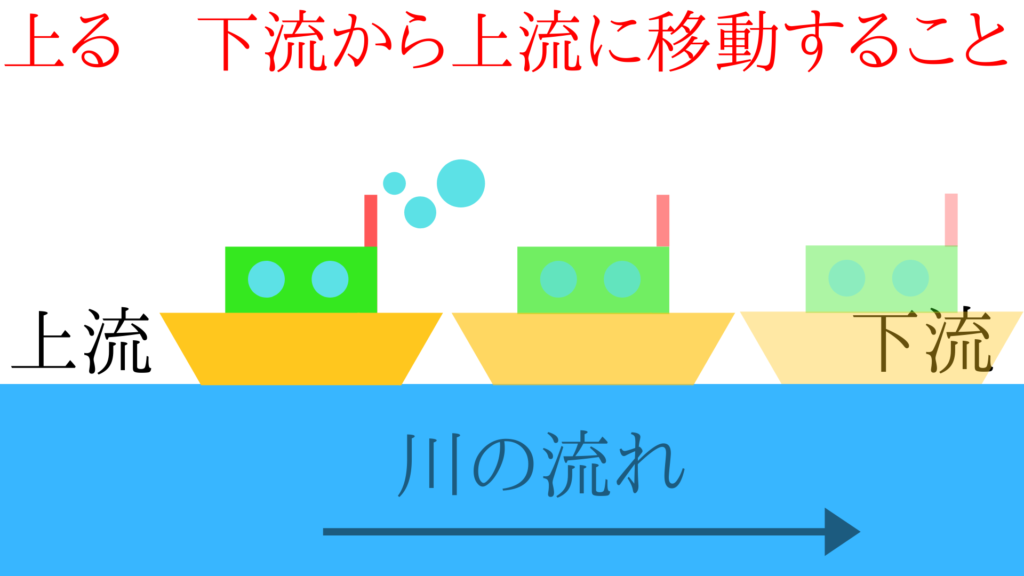
上流(川上)・下流(川下)の意味
上流(川上)・下流(川下)という言葉は、大人としては知っていて当たり前の言葉ですよね。
しかし、これが小学生になると何となくは分かっているけど、ぼんやりしていたり、実は分かっていなかったり・・・
まずはこの2つの言葉の意味が分かるのかを確認しましょう。

図のような関係がつかめていればばっちりです。
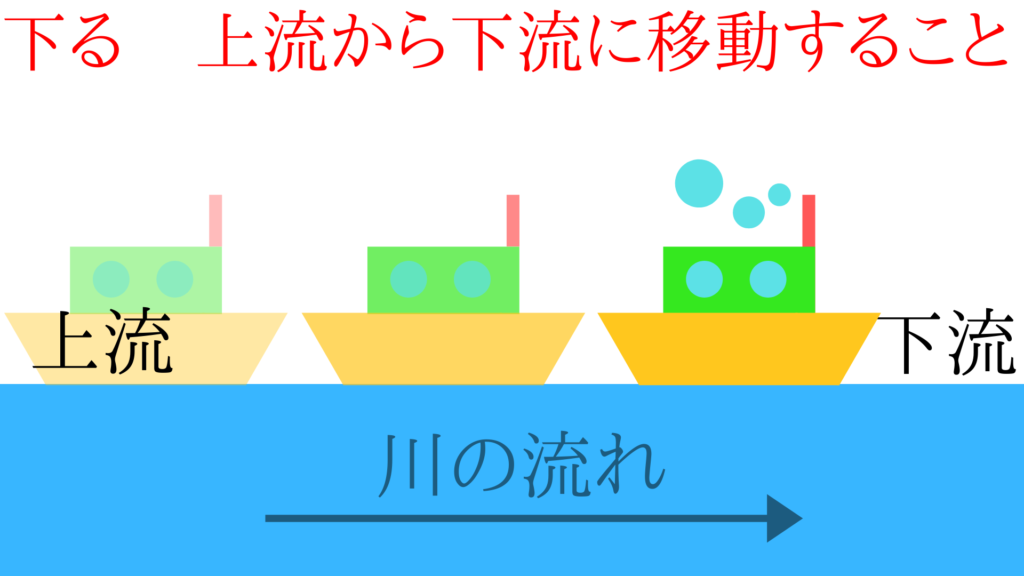
上る・下るの意味
上るというのは下流の方から上流の方に、下るというのいうのは上流から下流にの方に移動することです。
よくわかっていないことがあるのできちんと理解しているか尋ねましょう。
静水時の意味
流水算の単元で日常会話などで聞いたことがない言葉No.1なのがこの静水時という言葉です。
静水時と言うのは流れがない時と言う意味です。
川の上であっても、川というより池というイメージが作れれば大丈夫です。
川の上に船を浮かべたら流れることに対して、池に船を浮かべても流されませんよね。
池の上のような流れのないときと言う感じです。
ここまでの言葉、上流(川上)・下流(川下)、上る・下る、静水時を理解したら、流水算の速さの出し方をみていきましょう。
上り、下り、静水時の速さの出し方
上り、下り、静水時の速さの関係を理解しましょう。
上りの速さ=静水時の速さ-流水の速さ
下りの速さ=静水時の速さ+流水の速さ
静水時の速さ=下りの速さ-流水の速さ
=上りの速さ+流水の速さ
=\(\frac{上りの速さ+下りの速さ}{2}\)[1]上るときも下るときも川の流れの速さが同じ時にだけ使えます。川の流れる速さが上りと下りで異なるときは、線分図で処理しましょう。
このように書き出すと、公式のように見えてしまうかもしれません。
しかし、きちんと意味を理解した上で求められるのであれば丸暗記までする必要はありません。
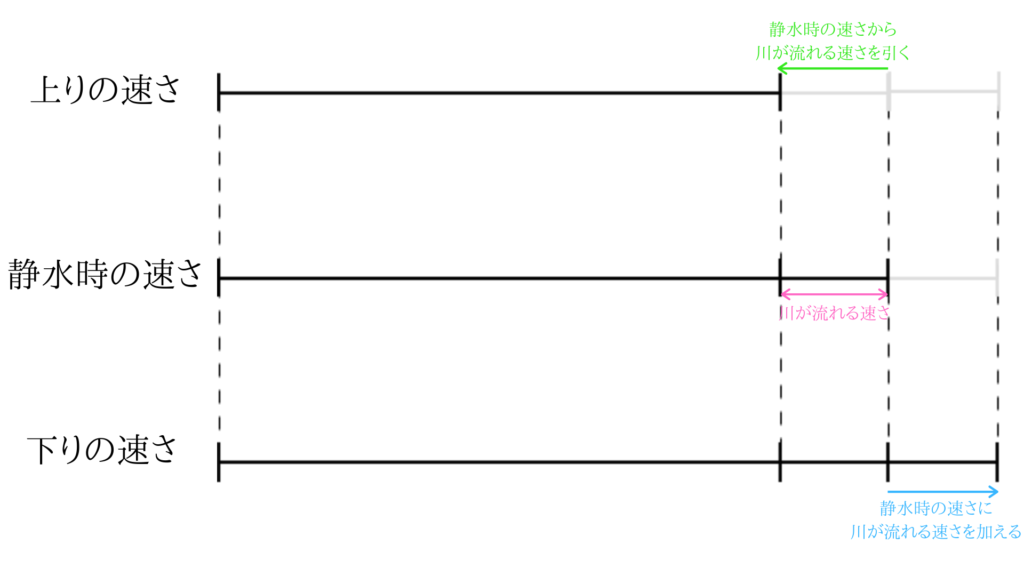
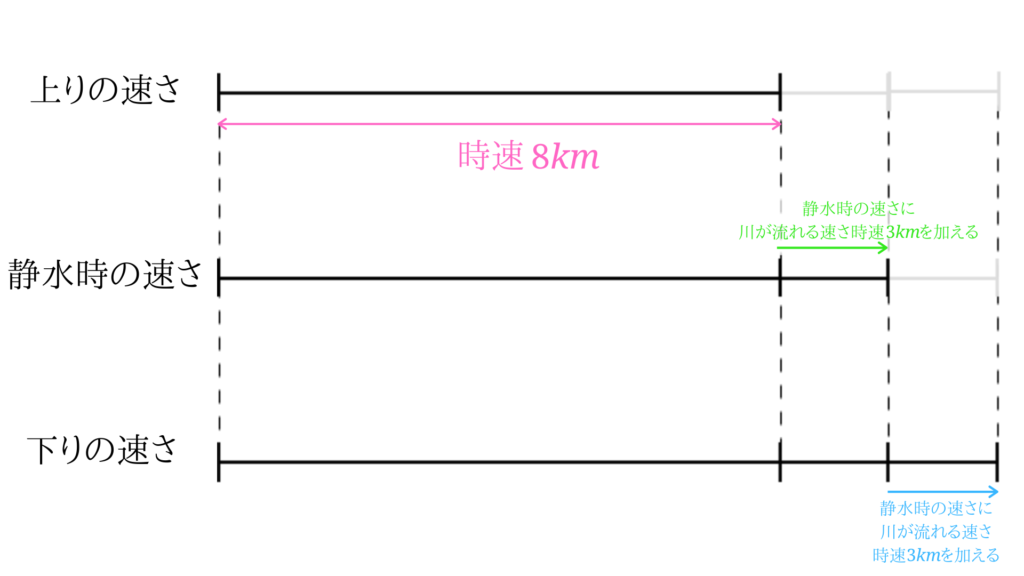
下の線分図の関係が分かっていればきちんと上り、下り、静水時の速さを求めることができます。
静水時の速さを基準に、上るときの速さと下るときの速さを考えると理解しやすいと思います。
上り、下り、静水時の速さを求めてみよう
簡単な例題を用いて、上り、下り、静水時の速さを求める練習をしてみます。
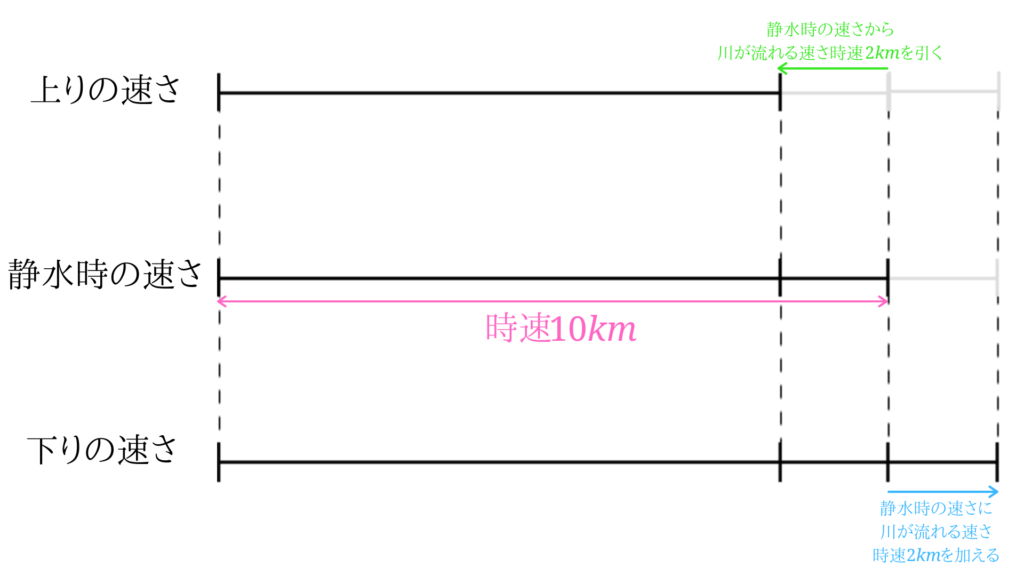
まずは上りの速さを求めましょう。
上りの速さは、静水時の速さから流水の速さを引くことで求めることができます。
静水時の速さは時速\(10km\)、川の流れる速さが時速\(2km\)なので、\(10-2=8\)となります。
上りの速さは、時速\(8km\)になります。
次に下りの速さを求めます。
下りの速さは、静水時の速さに流水の速さを加えることで求めることができます。
\(10+2=12\)となり、下りの速さは時速\(12km\)となります。
上りの速さと川の流れる速さが分かっています。
まずは静水時の速さを求めます。
上りの速さ時速\(8km\)から川の流れの速さ時速\(3km\)を加えればいいので、\(8+3=11\)となり、静水時の速さは時速\(11km\)となります。
さらに川を下る速さを求めます。
川を下る速さは、静水時の速さに川の流れる速さを加えればいいので、\(11+3=14\)となり、川を下る速さは時速\(14km\)となります。
上りの速さと下りの速さが分かっているときの静水時の速さを求めてみましょう。$$静水時の速さ=\frac{上りの速さ+下りの速さ}{2}$$
と、memoで書き出してみたのですが、単に覚えてこのことを使うというのは難しいかもしれません。
線分図で考えると、今回の静水時の速さも今までと同じように求めることができます。
線分図で上り、下りの速さを書き出してみます。
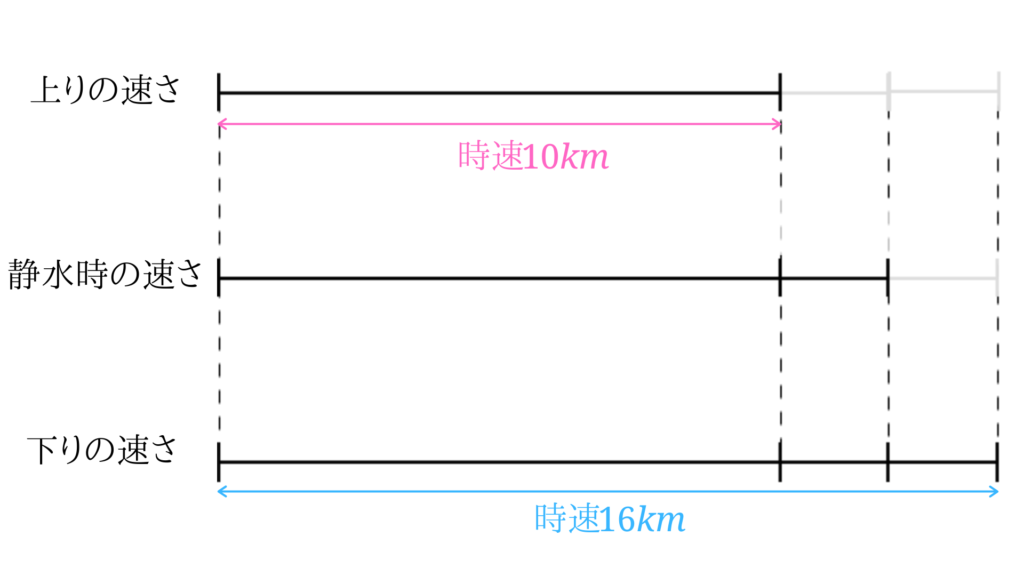
上りと下りの速さは問題文中に与えられているので、書き込んでみました。
上りの速さと下りの速さの差は、川の流れの速さの2倍になっていることが分かります。
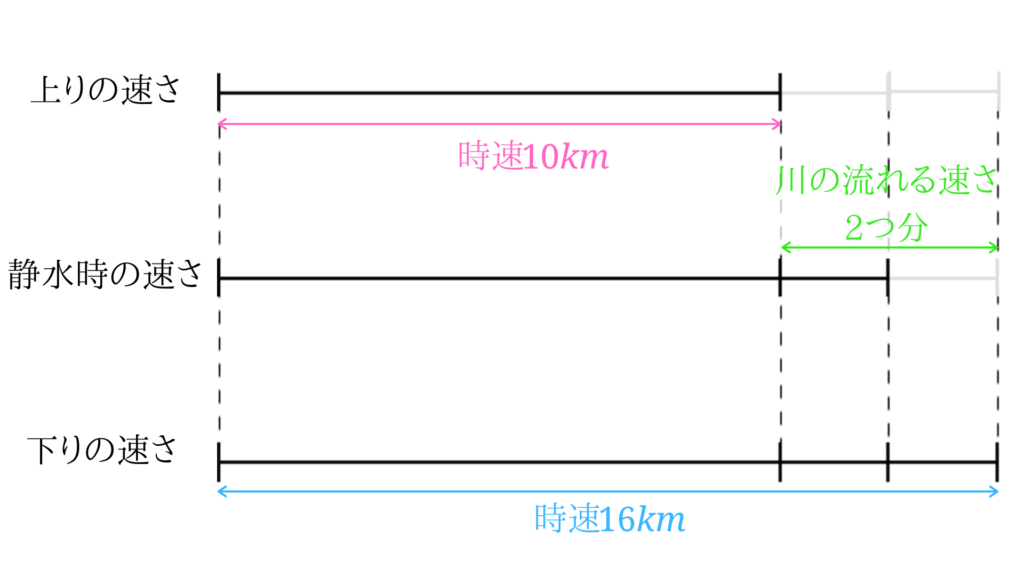
と、いうことは、下りの速さと上りの速さの差を2で割れば、川の流れの速さを求めることが出来そうです。
\( (16-10)\div 2=3\)となるので、川の流れの速さは時速\(3km\)になります。
あとは、上りの速さに川の流れの速さを足せば、静水時の速さを求めることができます。
\(10+3=13\)より、静水時の速さは時速\(13km\)と分かります。[2]下りの速さから川の流れの速さを引いて静水時の速さを求めてもOKです。そのときは、\(16-3=13\)という感じで求められます。
次に川の流れる速さが上りと下りで変わるときの静水時の速さの出し方も見てみましょう。
川の流れる速さが上りと下りで違う時の静水時の速さの求め方
先ほどの例題3を少し変えてみます。
川を上るときも下るときも、川の流れる速さが同じ問題と比べると難しそうに見えますね。
例題3改も、線分図を用いて解いていきます。
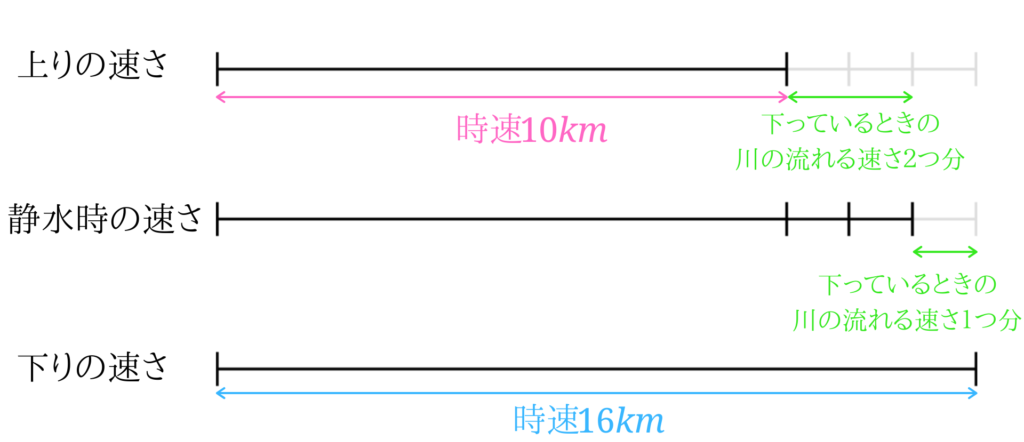
静水時の速さを基準に考えると分かりやすくなります。
上りの速さ=静水時の速さ-2×下っているときの川の速さ[3] … Continue reading
下りの速さ=静水時の速さ+下っているときの川の速さ
なので、線分図上で整理してみます。
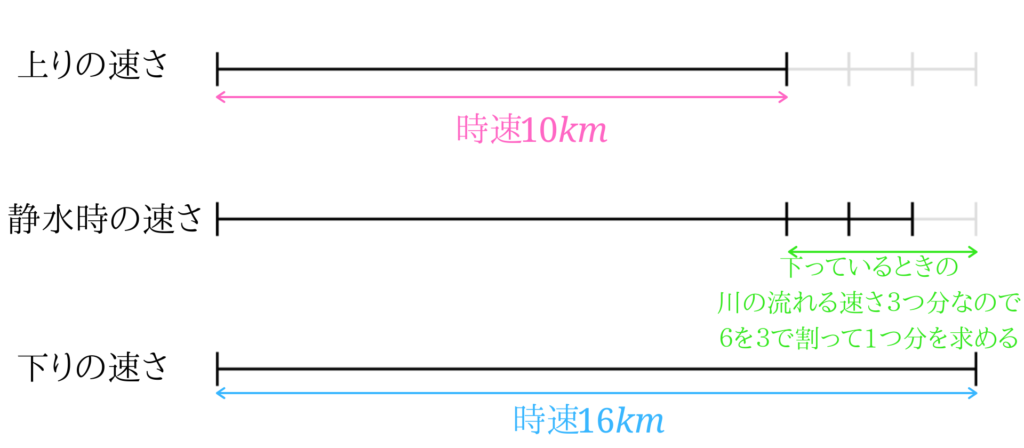
下っているときの川の流れの速さ1つ分を求めるには上りと下りの速さの差、6を3で割ればいいと分かります。
下っているときの川の流れの速さ1つ分は2となるので、静水時の速さは、\(16-2=14\)より、時速\(14km\)になります。
逆比を使った速さの求め方
今まで上り、下り、静水時の速さの関係からそれぞれの速さを求めました。
それぞれの速さが直接求められない問題を逆比を使って求めてみます。
問題文を見ると、分かっているのは、川の流れの速さと上りでかかった時間と下りでかかった時間だけです。
こんな風に時間が分かっているときは、速さの比から上りと下りの速さを求めることができます。
上りにかかった時間が5時間、下りにかかった時間が3時間なので、上りの速さと下りの速さの比は、3:5になります。
これを線分図で書いてみましょう。
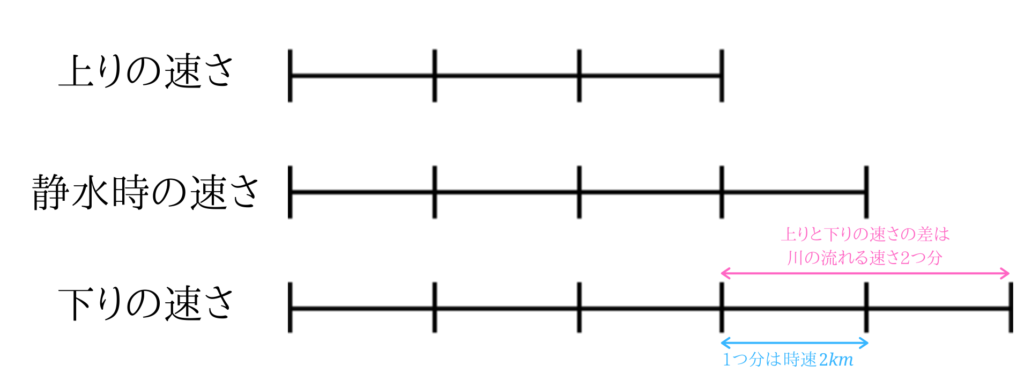
上りの速さと下りの速さの比の差は、川の流れの速さの2倍になります。
つまり、線分図の1区切りが示す速さは時速\(2km\)と分かりました。
このことから、
上りの速さ=時速\(2km\times 3=6\)
下りの速さ=時速\(2km\times 5=10\)
となり、上りの速さは時速\(6km\)、下りの速さは時速\(10km\)になります。
また、静水時の速さは時速\(8km\)です。
比が絡むので難しくなりますね。
ただ、逆比を使わないと求められないというものでもありません。
逆比を使わない方法でも上りと下りの速さを求めてみましょう。
逆比を使わない上りと下りの速さの求め方
逆比を使った線分図は速さを示していましたが、今度は距離の線分図を書いてみました。
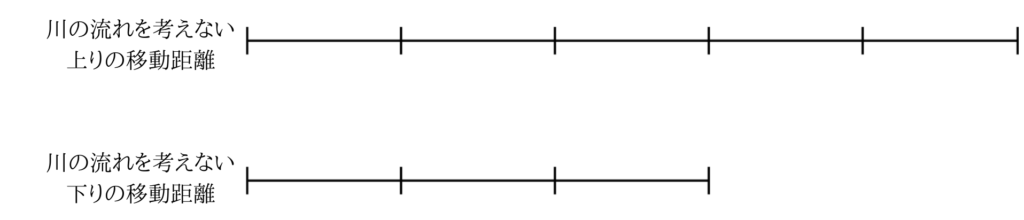
川の流れを考えずに、書いてみました。
ここから川の流れを加味していきます。
川を上る場合は川の流れに逆らうので、川の流れの分押し戻されます。
川を下る場合は川の流れに沿うので、川の流れの分押されます。
つまり、上りは川の流れの分移動した距離( 時速\(2km\times 5\) )が減り、下りは川の流れの分移動した距離( 時速\(2km\times 3\) )が増えます。
また、上りで移動した距離も下りで移動した距離も一致します。
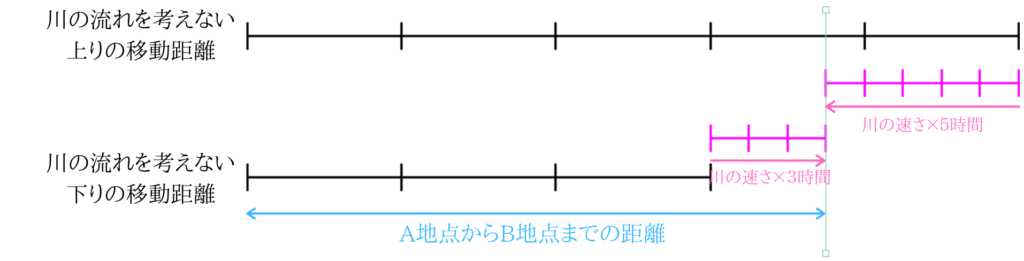
川の流れる速さは時速\(2km\)なので川の流れを考えない上りと下りの移動距離の差は\(16km\)となり、川の流れを考えない移動距離の線分図の1区切りが表す距離は\(=8km\)となります。
上りの距離を求めてから、上りの速さを求めます。
A地点からB地点までの距離\(=8\times 5-2\times 5=30km\)
上りの速さ\(=30\div 5=\)時速\(6km\)
あとは川の流れが分かっているので、
下りの速さ\(=6+2\times 2=\)時速\(10km\)となります。
逆比を使わずに速さを求めることができました。
川を上る船と下る船がすれ違う問題の解き方
次に流れる川で、2隻の船がすれ違う問題を解いてみましょう。
今までの問題との大きな違いは上りの速さも下りの速さも出すことができないことです。
川の速さが分からないので直接求めることができません。
ちょっと工夫をする、見方を変えないと答えを求められそうにありません。
上りの速さと下りの速さを考えてみます。
上りの速さ=静水時の速さ-川の速さ
下りの速さ=静水時の速さ+川の速さです。
2せきの船の1時間に近づく距離は、「上りの速さ+下りの速さ」になります。
上りの速さ+下りの速さ
=(静水時の速さ-川の速さ)+(静水時の速さ+川の速さ)
となります。
川の速さを相殺して、
=静水時の速さ+静水時の速さ
と分かりました。
つまり、この問題では、
1時間に\(5km\)ずつ2せきの船は近づくということになります。
A地点とB地点の間の距離は\(15km\)なので、
\(15\div 5=3\)
となり、出発してから3時間後に2せきの船がすれ違うことになります。
数式だけではイメージが湧かない時は
そんなときはちょっと視点を変えてみます。
流れのある川に2せきの船が浮いているだけの状態、川の流れに流されている感じをイメージしてもらえるといいと思います。
川の流れる速さは同じなので2せきとも同じ速さで流されていくので、2せきの船は近づきも、遠ざかることもありません。
この下流にある船が時速\(3km\)の速さでこの川を上るとします。
すると、この2せきの船は1時間に\(3km\)ずつ近づくことになります。
さらに上流の船が時速\(2km\)で川を下るとすると、2せきの船は1時間に\(5km\)ずつ近づきます。
2せきの船が川の流れに流されているところから考えるとイメージしやすいと思います。
こんな風に考えると、2せきの船が反対方向に進みすれ違う時間を求めるときには、川の流れる速さは関係ないことが分かります。
ダイヤグラム、グラフを読み取って上り、下り、静水時の速さを求める方法
最後にダイヤグラムやグラフからの静水時の速さの求め方をしてみましょう。
下のグラフは、ある船がA地点を出発し、上流にあるB地点までいき、A地点に戻ってくる様子を示したものです。
①川の流れの速さが一定であるとき、この船の静水時の速さを求めましょう。
②B地点からA地点に向かう時の川の流れる速さが、A地点からB地点に向かう時の川の流れの速さが4倍でした。この船の静水時の速さを求めましょう。

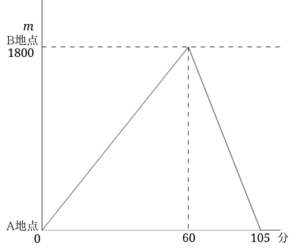
川の流れる速さが上りと下りで変わらない静水時の速さの求め方
まずはA地点からB地点の速さを求めます。
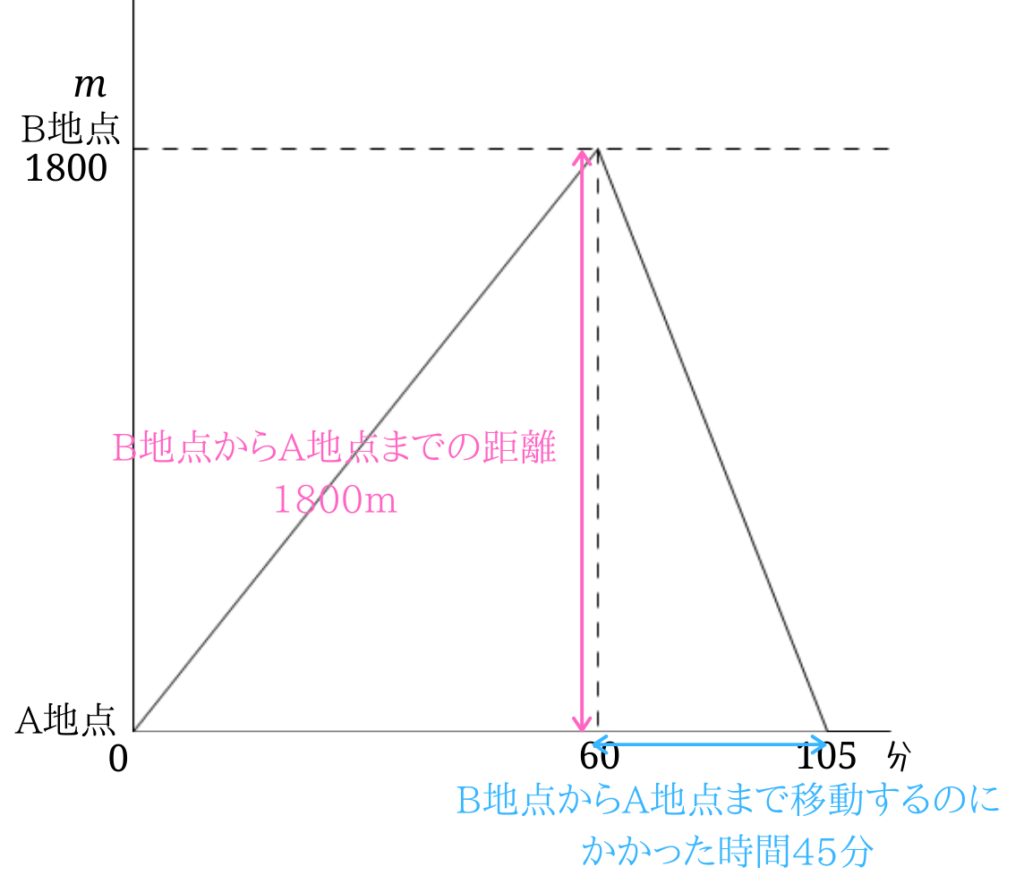
ダイヤグラムを見ると、A地点を出発したのが0分、B地点に到着したのが60分なので、
\(1800\div 60= 30\)となり、上りの速さは分速\(30m\)。
B地点からA地点の速さを求めます。
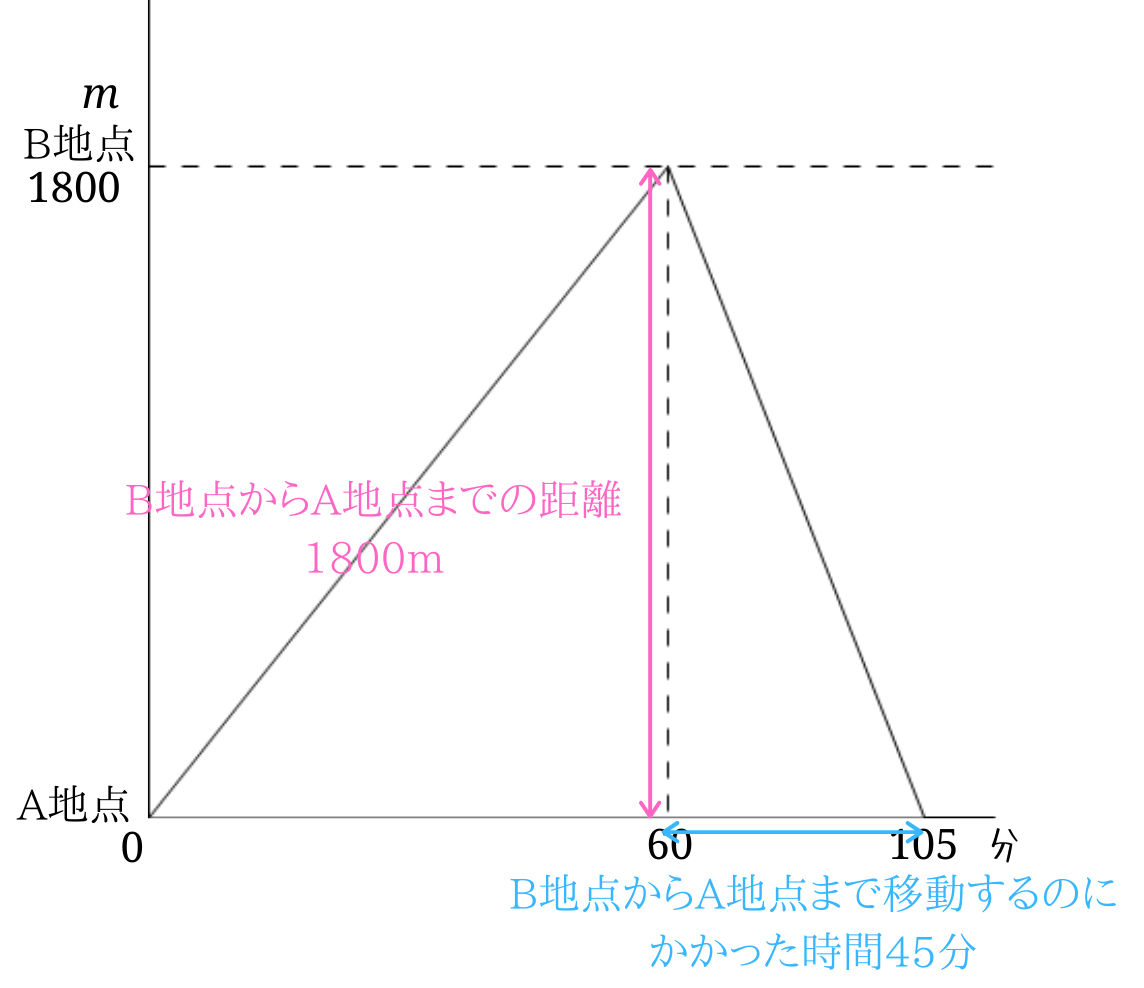
B地点を出発したのが60分、A地点に到着したのが105分。
B地点からA地点に行くのにかかった時間は、\(105-60=45\)で、45分。
このことから、B地点からA地点までの速さは、\(1800\div 45=40\)となり、下りの速さは分速\(40m\)。
上るときも下るときも川の流れの速さは同じなので、\( (30+40)\div 2=35\)となり、静水時の速さは分速\(35m\)となります。
線分図を使って静水時の速さを求める
上るときと下るときの川の流れる速さが同じ時は上りと下りの平均になるのですが、イメージがつかみづらいときは下のような線分図を書くと分かりやすいと思います。
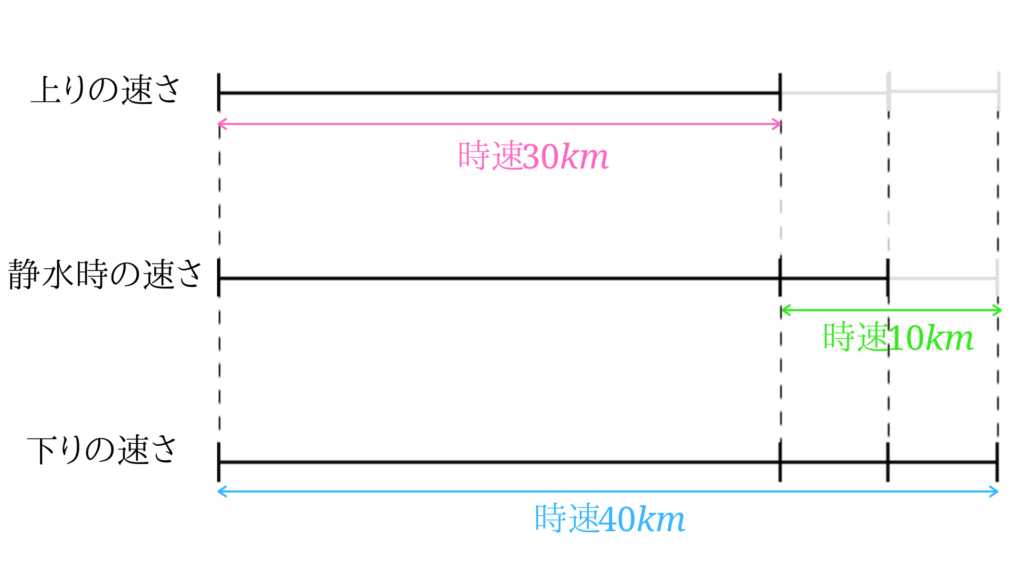
この図から、上りと下りの速さの差10を2で割り川の流れの速さ分速\(5m\)を求めて、あとは上りの速さに川の流れの速さ加えて、\(30+5=35\)より、静水時の速さは分速\(35m\)となります。
川の流れる速さが上りと下りで異なるときの静水時の速さの求め方
②の下るときの川の流れる速さが、上るときの4倍の場合の静水時の速さを求めてみましょう。
①では、上りと下りの川の流れる速さが同じだったので、簡単に平均をとってしまえば、静水時の速さを求めることができましたが、この問題では上りと下りで川の流れる速さが違うので線分図で考えましょう。
A地点からB地点までの速さとB地点からA地点までの速さは①の問題のときと同じです。
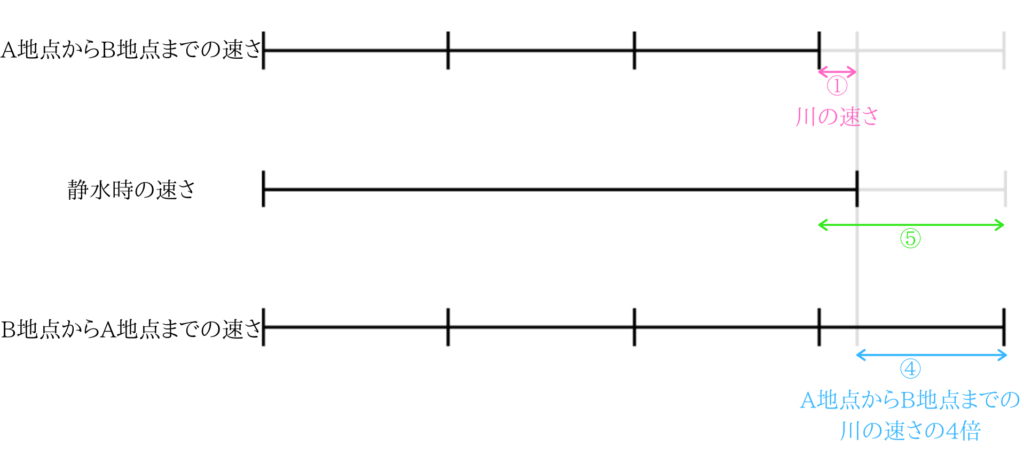
図の〇で囲んでいる数字は比を表しています。
ここまで線分図が書ければ、あとは川の流れを出すことが出来ればばっちりです。
上りと下りの速さの差10を5で割り、川の流れの速さが分速\(2m\)ということが分かります。
あとは上りの速さに川の流れの早さを足して、\(30+2=32\)となり、この船の静水時の速さは分速\(32m\)となります。
まとめ
流水算の基本的な速さの出し方についてでした。
流水算は川の流れがあるというだけで、複雑に見えがちです。
まずは言葉の意味、ここをきちんと押さえてもらいましょう。
言葉の意味が分かれば、次は上り、下り、静水時の速さです。
ここまでをきちんと求められれば、流水算特有の内容はほぼ終了です。
あとは、きちんと線分図を書き、情報を整理し、1つ1つ対処できれば、解けるようになると思います。
【関連記事はこちら】
・流水算の上りと下りの速さが分かっている時の静水時の速さと川の流れの速さの求め方とは
References
| ↑1 | 上るときも下るときも川の流れの速さが同じ時にだけ使えます。川の流れる速さが上りと下りで異なるときは、線分図で処理しましょう。 |
|---|---|
| ↑2 | 下りの速さから川の流れの速さを引いて静水時の速さを求めてもOKです。そのときは、\(16-3=13\)という感じで求められます。 |
| ↑3 | 一旦、「上りの速さ=静水時の速さ-上っているときの川の速さ」について考え、次に「上っているときの川の速さが下っているときの川の速さの2倍」を考えるとスムーズかもしれません。上りの速さが下りの速さの2倍になっていることから、下りの速さを基準に置くと楽になります。もちろん、上りの速さを基準にしてもいいのですが、下りを基準にした方が扱いやすいです。 |




