円周や円の面積を求めるときに使う円周率3.14ってなに？

円周=直径×3.14
円の面積=半径×半径×3.14
小学生であれば、よく見る公式ですよね。
公式なんだから覚えてしまえばよさそうなのですが、公式の中に数字がでてくるのは三角形や台形の面積の公式に登場する÷2くらいです。
それと比べても妙な数字3.14とは何なのでしょうか？

円周や円の面積を求めるときに使う円周率3.14ってなに？

円周率の3.14とは、円の直径を1としたときの円周の長さです。
どういうことかと言うと、直径:円周=1:3.14という意味になります。

つまり、直径の長さの3.14倍が円周の長さということになります。
そんなに難しいものではないのですが、このイメージがない子の方が多いと思います。
このイメージがあると、円周や円の面積の公式は覚えなくても、イメージのできる公式と早変わりするようになります。

円周率の定義から円周の公式を考える

もし、直径を3.14倍すると円周になるということをきちんと理解して覚えておけば円周の公式は当たり前の公式になります。
だって、直径を3.14倍すれば、円周を求められるんです。
つまり直径に3.14を掛けると円周になるということですよね。

直径×3.14が円周ということになるので、

円周=直径×3.14

ということが、普通に考えることで分かるようになります。
円周率3.14が直径に対する円周の比ということが分かることで、円周の公式は当たり前のものとなります。

円周率の定義から円の面積の公式を考える。

次に円の面積の公式を考えてみましょう。

円を長方形にして円の面積の公式を求める方法

図のような６等分に切れ目が入っている円があるとします。

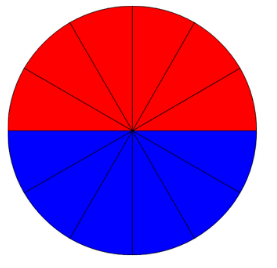
この円を切って並べてみます。
するとこんな感じになりました。

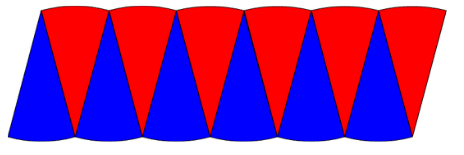
さらに細かく円を切ってみます。
次の図は円を24等分にしたものです。
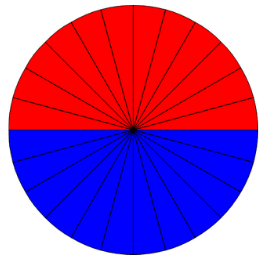円を24等分にして先程と同じように並べてみます。

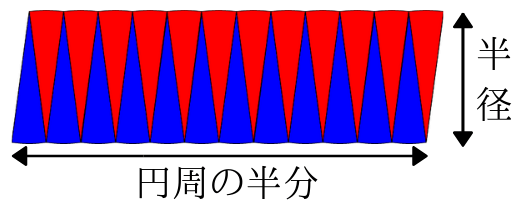
細かく円を切断してならべてみると、先程の12等分したときよりも長方形に近くなってきました。
もっと細かく切っていくと、長方形に近づいていきます。

この長方形の縦の長さが半径、横の長さが円周の半分に当たります。
また長方形の面積は縦×横なので、半径×円周×\(\frac{1}{2}\)ということが分かります。
円周は直径×3.14なので、半径×直径×3.14\(\frac{1}{2}\)
さらに、直径は半径×2なので、半径×半径×3.14となります。

このことから、円の面積=半径×半径×3.14となります。

円を三角形にして円の面積の公式を求める方法

図のような円があるとします。
先ほどは円をぶつぶつ切ってみましたが、今度はちょっと見方を変えてみます。
今度は、中身まで詰まったバームクーヘンみたいな感じで考えみましょう。
こんな感じです。

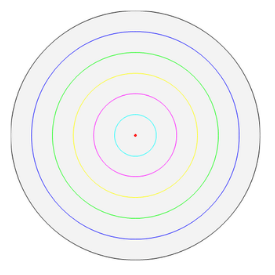
このバームクーヘン状の円に切れ目を入れてみましょう。
一番上から真ん中まで切れ目をいれる感じです。

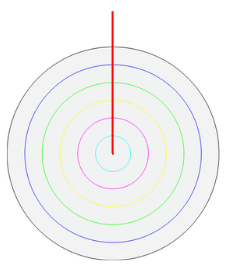
次にそのまま切れ目の部分から円を開いていきます。
開いたら図のように、バームクーヘンをぺたんこに開いてみます。

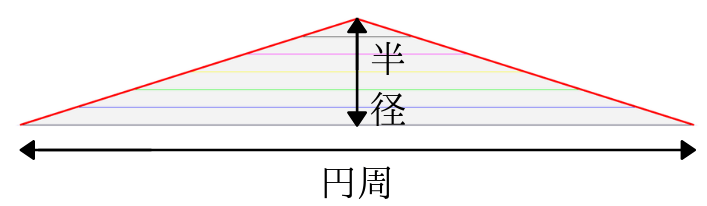
すると二等辺三角形ができました。
この二等辺三角形の面積が円の面積と言えそうです。
二等辺三角形の面積を求めるには、底辺×高さ÷2となります。
つまり円周×半径÷2ということが分かります。
また円周は直径×3.14=半径×2×3.14なので、円の面積は半径×半径×3.14となります。

まとめ

円周率3.14とは何なのかということについて書いてみました。
なんとなく公式の中にあった3.14という数字が、円の直径と円周の比のことだと分かることで分かることがたくさんでてきました。
単に暗記だけしていくと公式がどんどん増えていってしまい、何をしているのか分からないということになりがちです。
円周率は分かってしまうと読んだままの意味なのですが、お子さんたちは知りません。
おそらく学校の導入では習っていると思うのですが、問題を解いているうちに単なる公式中の数字に成り下がってしまいます。
円周を求める公式と円の面積を求める公式を混同してしまうお子さんが多いところから見ても円周率の意味がしっかり分かるというのはとてもためになると思います。
しっかり円周率の意味から円周を求める公式、さらには円の面積の公式までしっかりイメージづけることができるといいですね。
・面積のまとめへ戻る