時計算の解き方や教え方を解説！長針と短針が1分間に動く速さがポイント！

速さの問題の中でも変わっているのがこの時計算。
よく中学受験でも出題されます。
特別に覚えるべきことがないので、きちんと理解すれば意外とすんなり解けてしまいます。
この記事では時計算が解けるようになることを目指します。

時計算では長針と短針が1分間に動く角度が大切！

時計算は旅人算の時計バージョンという感じです。
題材が時計なので、そんなにややこしくするということも難しいので、基礎的なことができれば十分対応できます。
大きな違いは1分間に進む距離などで速さを表していたのが、1分間に進む角度で表すことくらいでしょうか。
それでは時計算のポイントを例題を元に理解しましょう。

①の問題は長針が1分間に動く速さに当たります。
長針は60分で時計を1周します。
1周は360度なので、360を60で割ることで、長針が1分間に進む速さを求めることができます。$$360\div 60=6$$となり、長針は1分間に6°進みます。
①の答えは6度と分かりました。

次に②です。
②は短針が1分間に進む速さに当たります。
短針は1時間(60分)の間に、30度^[1]短針は12時間で時計を1周するので、\(360\div 12=30\)で、短針が1時間に進む角度を求めることができます。進みます。$$30\div 60=0.5$$となり、短針は1分間に0.5度進みます。
②の答えは0.5度と分かりました。

長針と短針の動く速さが、時計算を解く上で外せない基礎になるので、きちんと求められるようするといいと思います。

長針と短針が重なる時刻の求め方

それでは時計算の基本的な問題を解いてみましょう。

まず考えるのは4時の時の長針と短針のなす角を考えましょう。
時計の文字盤上の数字の0から4までの間なので、360度の\(\frac{4}{12}\)になります。
つまり、\(360\times \frac{4}{12}\)を計算して、長針と短針のなす角は120度ということになります。

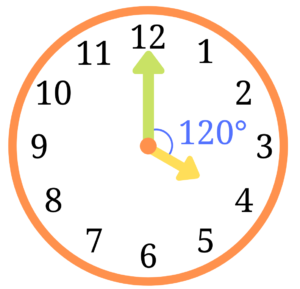
長針と短針が重なるまでにどれだけの時間がかかるかを求める問題です。
どんな状況になれば短針と長針が重なるのかを理解することが大切です。
長針と短針が重なるというのは、4時の時点で120度先に進んでいる短針に長針が追いついた時のことになります。

ここで、長針と短針が1分間にどれだけ追いつくのかを考えます。
長針は1分間に6度、短針は1分間に0.5度動きます。
このことから長針と短針の間は1分間に5.5度ちぢまるということになります。

つまり、4時の時点で短針が長針に比べて120度先行している状態から、1分間に5.5度ずつ差が縮みます。
追いつくまでにかかる時間は、\(120\div 5.5=\frac{120}{5.5}=\frac{240}{11}\)となり、長針と短針が重なる時刻は\(4\)時\(\frac{240}{11}\)分(\(9\)時21\(\frac{9}{11}\)分)と分かります。

次は時計の長針と短針がちょうど一直線になる場合を考えてみましょう。

長針と短針のなす角がある角度になるときの時刻の求め方

次に②の「長針と短針がなす角が初めて180度になる時刻」を求めてみましょう。

長針と短針と2つのものが動く速さになるので、うまく工夫をして解いていかないと難しくなります。
長針と短針のなす角が180度になるということが、どういうことなのかを考えます。
4時時点の長針と短針のなす角は120度でした。

これから時間がすすんでいくと、この角度は1分ごとに5.5度ずつ長針が短針に追いていきます。
長針が短針に追いつくまでの長針と短針のなす角は、120度から0度まで同じ割合で減っていきます。
その後長針が短針を追い抜き180度差がついた時刻が答えになります。

つまり、長針が短針よりも\(120+180=300\)度、多く移動すればいいということになります。

このことから、\(300\div 5.5=\frac{300}{5.5}=\frac{600}{11}\)となります。
時計と長針と短針のなす角が180度になるのは\(4\)時\(\frac{600}{11}\)分ということが分かります。

長針と短針がある直線に対して線対称の位置関係になるときの時刻の求め方

次に長針と短針がある直線について線対称の位置になるときの時刻を求める問題です。
どういう状態になった時の時刻を求めるのかというと下の図のような感じになったときの時刻になります。

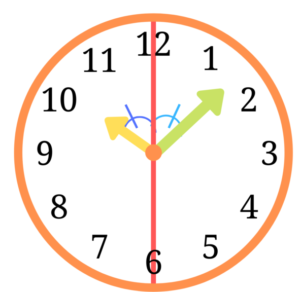
短針と真ん中にある直線なす角と長針と真ん中の直線のなす角が等しくなった時が長針と短針が線対称の位置にある時です。
しかし、短針と直線とのなす角は1分間に0.5度ずつ減少することに対して、長針と直線のなす角は1分間に6度ずつ増加していきます。
方程式だと求めやすそうですが、このまま計算することは難しそうです。
ここでちょっと工夫して線対称になるときの時刻を求めます。

短針を対称移動して長針と短針が一致する時刻を求める方法

そのままでは求めにくいので、短針を直線の反対側に移動させます。
時間がたつと短針は矢印の方向に移動します。
右側にある短針は、左の短針の線対称の位置関係にあるので、反時計回りにまわります。^[2] … Continue reading

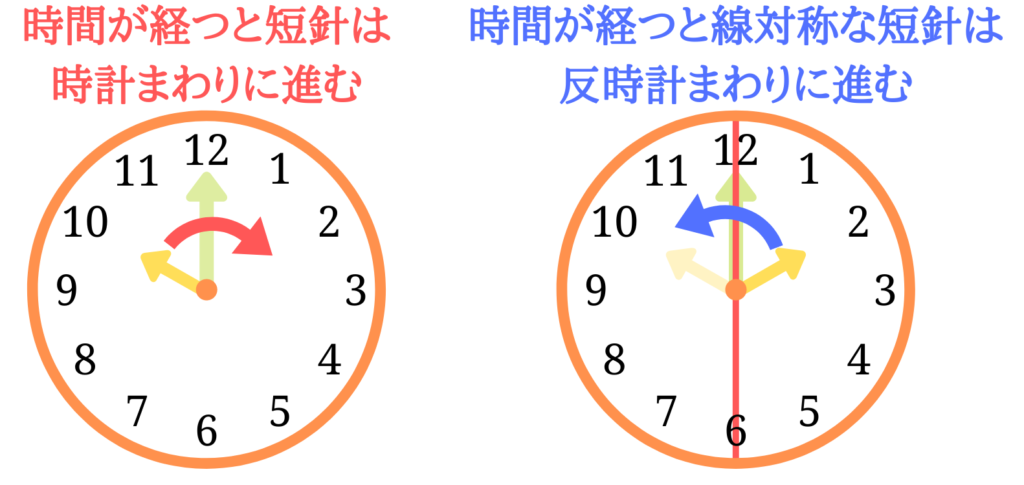
また常に左の短針と直線のなす角と右の短針と直線のなす角は等しくなります。
つまり、右の短針と長針が重なった時刻が、短針と直線のなす角と、長針と直線のなす角が等しくなる時刻だと分かります。

長針は時計廻りにに1分間に6度、右の短針は反時計回りに1分間に0.5度進みます。

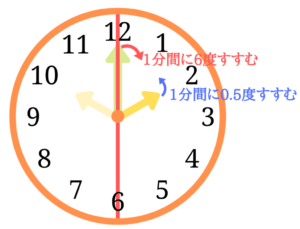
つまり、4時時点の短針と直線のなす角は60度です。
長針と右側の短針は1分間に\(6+0.5=6.5\)度近づくので、\(60\div 6.5=\frac{120}{13}\)となり、長針と短針が直線と線対称な位置関係になるのは、\(4\)時\(\frac{120}{13}\)分と分かります。

長針と短針が線対称の位置、左右対称になったところから求める方法

長針と短針の4時の位置と線対称になった状態から求めることもできます。
図のように4時の長針と短針の位置と長針と短針が左右対称になった位置を書きます。

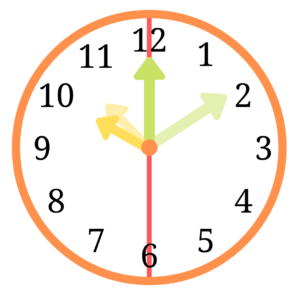
長針と短針の動く速さの比は、0.5:6なので、4時の短針と左右対称になったときの短針のなす角と直線と左右対称になったときの長針のなす角の比は、0.5:6となります。

また、長針と短針の位置関係が左右対称になったときなので、4時の短針と直線のなす角と直線と4時の長針のなす角は等しくなります。

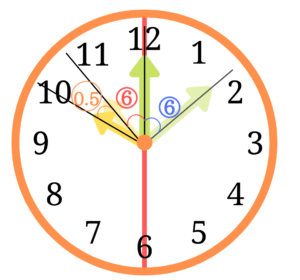
このことから①当たりの角を求めます。
\(60\div (0.5+6)=\frac{60}{6.5}=\frac{120}{13}\)度となります。
長針は⑥動いているので長針が動いた角度は、\(\frac{120}{13}\times 6=\frac{720}{13}\)度。

長針がこの角度を動くのにかかった時間を求めます。
長針は1分間に6度動くので、\(\frac{720}{13}\div 6=\frac{120}{13}\)分。
長針と短針が時計の文字盤の12と6を結んだ直線について線対称の位置関係になるのは\(9\)時\(\frac{120}{13}\)分になりました。

まとめ

時計算について書いてみました。

時計算の要はなんと言っても長針と短針の動く速さです。
速さでは分速〇kmのように長さで表されていましたが、時計算では角度で表すのではじめのうちはやりにくく感じてしまうお子さんもいます。
この部分をクリアにすることが時計算を攻略する一歩になります。
単に長針は1分間に6度、短針は1分間に0.5度と覚えるのではなく、きちんと時計の性質から計算で出せるようにするのがオススメです。
この部分を暗記で乗り越えてもそのあとで分からなくなりがちです。
せっかくのお勉強する題材になるのでしっかり理解しながらすすめていくといいと思います。

【関連記事はこちら】
・旅人算が苦手を克服！分かりやすく教える方法や解き方とは