算数の割り算の包含除を使った余りの意味の考え方

算数で最も躓きやすいのが割り算です。

今回の記事では包含除の考え方を使って割り算の余りの意味について考えてみたいと思います。

算数の割り算の余りを包含除を使って考えてみよう

割り算の包含除という概念をご存じでしょうか。
端的に言うと、割られる数の中に割る数がいくつ入っているかという考え方です。
例えば\(8\div 4=2\)を元に考えてみると、8の中に4は2つ入っているという考え方です。

それでは、例題を使って割り算の余りの意味を包含除を使って考えてみましょう。

まずは、\(6\div 2=3\)から考えてみます。
6のなかにいくつ2のかたまりが入っているのかを考えます。

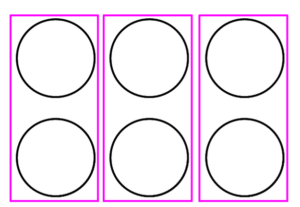
2のかたまりが3つあるので、答えが3ということになりました。

次に、\(7\div 3=2\cdots 1 \)について考えみます。
さきほどと同じように、3のかたまりがいくつあるのかを考えます。
3のかたまりを作っていくと、

3のかたまりを2つ作ることが出来ました。
この時、3のかたまりができなかったところがありますね。

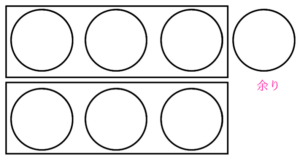
このかたまりをつくることができなかった部分が余りになります。
整数の範囲だと包含除の余りは考えやすいかもしれません。

小数第一位まで答えを求めたときの余りは包含除では、どう解釈したら良い？

さらに少し拡張して考えてみます。
今度は\(\frac{1}{10}\)の位まで答えを求めたときの余りを包含除を使って解釈してみましょう。

1の位の計算は先程の(2)\(7\div 3=2\cdots 1\)と同じように考えれば大丈夫です。

余りが1なので割る数3のかたまりはもう1つも作ることが出来ません。
そこで、割る数3の0.1個をもとに考えます。
割る数の0.1個は、0.3なので、0.3がいくつ1の中にいくつ作ることが出来るかを考えます。^[1] … Continue reading

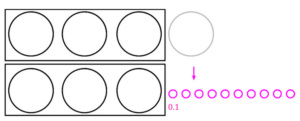
また、余りの1を0.1の丸に直してみました。
こうすることで、0.3のかたまりを作りやすくなります。
0.3のかたまりを作ると、3つ0.3のかたまりを作ることが出来ました。

0.3のかたまり1つは、3のかたまりの0.1個に当たります。
つまり0.3のかたまりが3つ出来たということは、0.3を意味します。
0.3のかたまりを作ったときに余った0.1は余りということになります。

\(7\div3\)を小数第一位まで求めて余りを出すと、\(7\div 3=2.3\cdots 0.1\)となります。

まとめ

今回の記事では、算数の割り算の余りの意味を包含除の考え方で考えてみました。

単に計算をするというときにはあまり役に立つ事はないかもしれません。
しかし、以外とこの考え方が役に立ってくれるのが文章問題を解く場合です。
特に割り算の式の立式は思いの外難しいです。

さらにお子さんに説明するとなると、なぜ割り算の式になるのかを伝えるのはかなり難度の高いことです。
また、きちんと説明してもなかなか理解できないということもあります。
きちんと割り算の余りが出るときまで、何をしているのかということがイメージできると文章問題でもきちんと対応することができるようになります。

地味なところですが、きちんと理解すると後々まで役に立つ知識になってくれますよ。

【関連記事はこちら】
・割り算の等分除と包含除の意味と違いの教え方とは？