割り算の2つの概念のうちの1つが等分除。
○等分したときの1つ分が商としてでてくるという理屈なので、割り算の理屈としてはイメージがしやすい考え方です。
6÷2のような自然数同士の割り算であれば、6を2等分するというイメージもしやすいのですが、\(6\div \frac{1}{2}\)のように割る数が分数になったり、\(6\div 0.2\)のようになってしまうと、もはや何をしているのかイメージするのも難しくなってしまいます。
今回の記事では、割り算の理屈の1つの等分除を小数や分数まで拡張したときの意味について書いてみたいと思います。
等分除を整数範囲だけでなく分数や小数まで拡張して意味を考えよう!
まずは割り算の理屈をしっかり呑み込みましょう。
最初は自然数同士の割り算で考えるとイメージがしやすいです。
まずは、正の整数同士の割り算のイメージがつかめたら、今回の本題、等分除を分数や小数に拡張して考えたときにどうすると割り算が何をしているのかをイメージしやすいのでしょうか。
まずは自然数同士の割り算を考えて、しっかり割り算が何をしているのかをつかみましょう。
\(6\div 3\)を例に考えてみましょう。
\(6\div 3\)を等分除で考えると、6を3つのグループに分けるという意味になります。
計算してみると、\(6\div 3=2\)となります。
このとき商として出てきた2は、1グループにいくつなのかということになります。
\(6\div 3=2\)をもう少し詳しく見ていきます。
3が意味するのは3つのグループに分けますよという意味ですね。
2が意味するのは3等分したときの1つのグループの数ということになります。
こう見ていくと6は何を意味するのでしょうか。
2の意味を3等分したときの1つのグループの数とみると、6は3グループを合わせた数を意味すると考えることができます。

分数にまで数を拡張したときの等分除の解釈
今度は、\(6\div \frac{1}{3}\)について考えてみます。
今までの通りに素直に等分除の考え方に当てはめて考えてみましょう。
すると、\(6\div \frac{1}{3}\)の意味は「6を\(\frac{1}{3}\)等分にする」ということになります。
なかなかイメージするのが難しいですよね。
\(\frac{1}{3}\)等分ってどういうことを言うのでしょうか。
考えれば考えるほどなんだかよく分からなくなってしまいます。
先ほどの、\(6\div 3=2\)と同じように解釈してみましょう。
\(6\div \frac{1}{3}\)の\(\frac{1}{3}\)は○等分という意味だったので、\(\frac{1}{3}\)等分にするという意味だととりあえず解釈しておきます。
さらに6について考えてみると、6は「1つのグループの\(\frac{1}{3}\)が6」ということになります。
さらに商は○等分したときの1つのグループの数です。
つまり、\(6\div \frac{1}{3}\)の答えは、6を3倍すればいいということになるので、答えは18ということが分かります。
小数でも同じように考えてみよう
\(6\div0.2\)を使って等分除で考えてみましょう。
\(6\div0.2\)をそのまま読み解いてみると、「6を0.2等分する」というように見えます。
そうは言っても何のことか分かりません。
小数も分数と同じで、割られる数の解釈がポイントです。
つまり、この\(6\div0.2\)の式の6が意味するのは「1つのグループの0.2が6」ということになります。
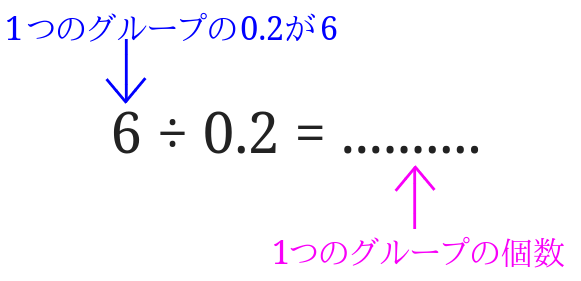
1グループに入っている数を求めれば良いので、\(6\times 5=30\)となりました。

まとめ
今回の記事では、割り算の理屈の1つの等分除を小数や分数まで拡張したときの意味について書いてみました。
割る数を元に等分除の考え方で考えると、6を\(\frac{1}{3}\)等分しようと考えてみても、6を0.2等分しようと考えてみてもなんのことかよく分かりません。
そこで割られる数の意味をきちんと考えることで、割り算の割る数が小数や分数になってもきちんと説明がつきます。
「割られる数」が「割る数のグループ内にある数」とみることができると綺麗に説明ができるようになりました。
【関連記事はこちら】
・割り算の等分除と包含除の意味と違いの教え方とは?




