長方形や正方形のような図形の面積はなぜ面積が求められるのかのイメージがしやすいのですが、三角形になるとイメージしづらくなりがちです。
三角形の面積を求めるには底辺×高さ÷2でできるといえばできますが、与えられた数字が3つだったり、4つだったりすると話が変わってきます。
今回の記事では、なぜ底辺×高さ÷2で求められるのかということについて書いてみたいと思います。
三角形の面積はなぜ底辺×高さ÷2で求められるの?
三角形は大きく分けて3種類あります。
直角三角形[1]3角形の角のうち1つが90°である三角形のことをいいます。、鋭角三角形[2]三角形の3つの角、全てが90°より小さい三角形のことをいいます。、鈍角三角形[3]三角形の角のうち1つの角が90°より大きい三角形のことをいいます。です。
1つ1つ、三角形の面積が底辺×高さ÷2で求められるのかみていきましょう。
まずは直角三角形からみていきましょう。
なぜ直角三角形の面積は底辺×高さ÷2で求められるの?
それでは直角三角形の面積が底辺×高さ÷2で求められるのかやってみましょう。
次の直角三角形の面積を求めましょう。
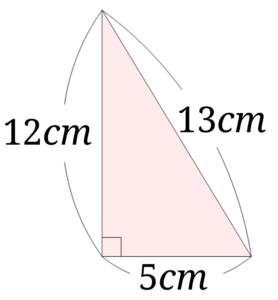
求めるには$$5\times 12\div 2=30$$として、答えは\(30cm^2\)となります。
それでは順番にみていきます。
まずは最初の\(5\times 12\)を考えてみます。
\(5\times 12\)がどこを表しているのかというと、下の青色の部分の面積となります。
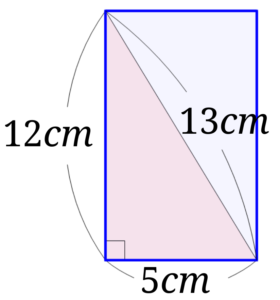
1辺が\(5cm\)、\(12cm\)の長方形の面積ということが分かります。
次にこの長方形は、もとの直角三角形を2つ合わせた図形とみることもできます。
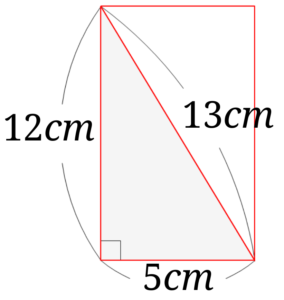
つまり、この長方形の面積はもとの直角三角形の面積2つ分ということになります。
あとは、直角三角形1つ分の面積にするために2で割って、直角三角形の面積が求められることが分かります。
このことを数字を入れずに考えてみましょう。
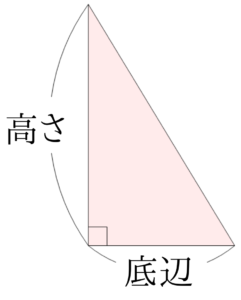
底辺×高さは下の図の長方形の面積になります。
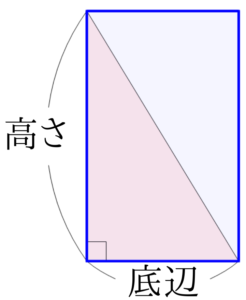
この長方形の面積は直角三角形の面積の2倍なので、求める直角三角形の面積は底辺×高さ÷2ということになります。
鋭角三角形の面積が底辺×高さ÷2で求められる理由
次の鋭角三角形の面積を求めましょう。
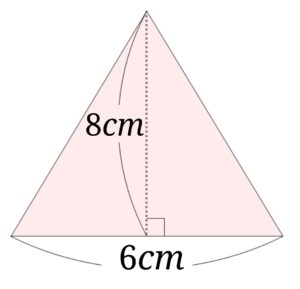
小学生にとって三角形というと真っ先に思い浮かべるのが鋭角三角形だと思います。
まずはこの面積を求めてみましょう。$$6\times 8\div 2=24$$となります。
直角三角形の時と同じように、計算式が何を意味しているのかをみていきます。
まずは最初の\(6\times 8\)のところですね。
\(8cm\)が底辺の中途半端なところにあるので、イメージしにくいので、\(8cm\)をずりずりっと底辺の左端まで持って行きます。
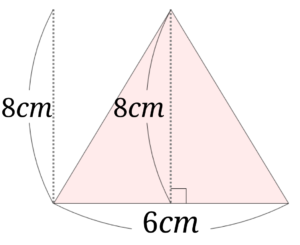
\(6\times 8\)を底辺の\(6cm\)と左側の\(8cm\)を掛けたと考えると、
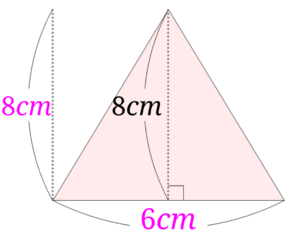
縦の長さが\(6cm\)横の長さが\(8cm\)の長方形の面積ということになります。
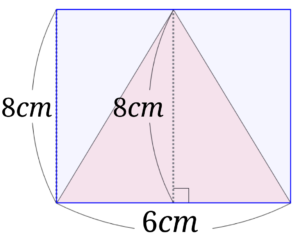
さらに、この長方形をしたの図のように4つの三角形の部分に分けて考えみます。
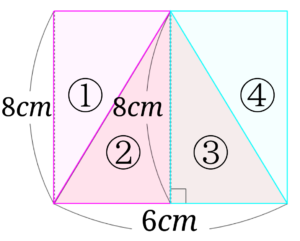
すると、図の①の三角形と②の三角形、③の三角形と④の三角形は合同[4]大きさも形も同じ三角形です。です。
先程の長方形の面積は、元の三角形の面積を2倍したものということが分かるので、長方形の面積を半分にするために、2で割ればいいということになります。
長方形の面積を2で割って、\(6\times 8\div 2\)として、答えは\(24cm^2\)ということになります。
このことを、数字(長さ)を入れずに考えてみます。
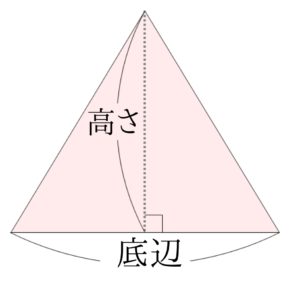
底辺×高さは下の長方形の面積になります。
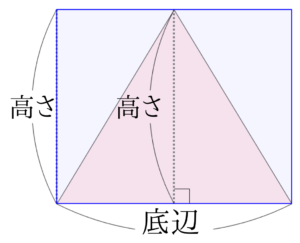
この長方形の面積は求める鋭角三角形の面積2倍なので、鋭角三角形の面積は底辺×高さ÷2ということになります。
少し直角三角形よりも難しくなりましたね。
次は鈍角三角形について考えてみます。
なぜ鈍角三角形の面積は底辺×高さ÷2で求められるの?
またまた例題を使って考えます。
次の直角三角形の面積を求めましょう。
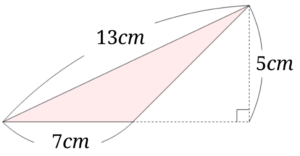
まずは面積を求めてみましょう。$$7\times 5\div2 =17.5$$となり、求める鈍角三角形の面積は\(17.5cm^2\)ということになります。
底辺×高さ÷2のイメージがつかみにくいのが、この鈍角三角形の面積を求める場合です。
高さが三角形の外にあるのでなんだか変な感じがしてしまうのがその原因でしょうか。
下の図のように、与えられた数字に加えて、横の長さを使って考えて思います。
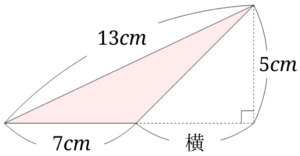
(横\(+7\) )\(\times 5\)の面積をもとに考えていきましょう。
この面積は図の部分になります。
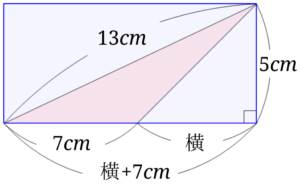
求める鈍角三角形と右下にある直角三角形の面積を合わせた面積は長方形全体の面積の半分です。
ここでは、元の長方形の下半分(濃い青色の部分)とします。
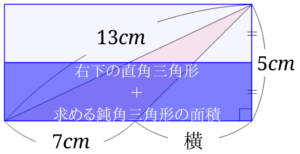
求める鈍角三角形の面積と右下の直角三角形の面積を合わせたものが、全体の長方形の半分なので、もとの長方形の下半分=求める三角形+右下の直角三角形を使って考えます。
長方形の下半分の面積から右下の直角三角形の面積を引いたときの残りの面積が求める三角形の面積となります。
下の図の2つの青い直角三角形は合同[5]形も大きさも同じということです。です。
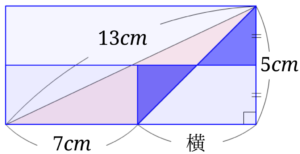
このことから、赤の長方形と右下の直角三角形の面積は同じということになります。
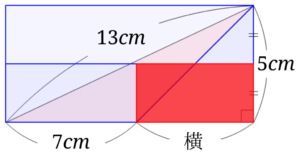
と、いうことは、もとの長方形の下半分の面積から、赤の面積を差し引いた残りの部分が求める鈍角三角形の面積ということになります。
求める鈍角三角形の面積は、\(7\times 5\div2\)ということになります。
\(\div 2\)の部分は、求める鈍角三角形の面積と等しい長方形の縦の長さが元の長方形の縦の長さ半分というところから来ています。
このことを数字を入れずに考えます。
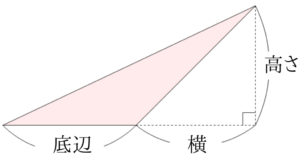
求める鈍角三角形の面積と右下の直角三角形の面積の和は、下の図の赤い長方形の面積の半分です。
赤い長方形の下半分の青い部分を求める鈍角三角形と右下の直角三角形の和として考えます。
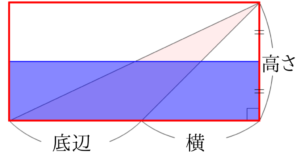
次に図のように、右下の直角三角形の下の長方形からはみ出た部分を切り取り、下の図のように移動させます。
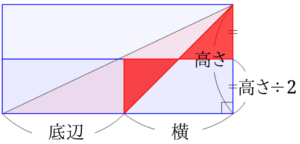
求める鈍角三角形の面積は、図の赤い長方形の面積と等しいことが分かります。
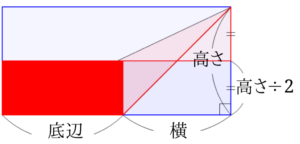
赤い長方形の縦の長さは高さ÷2、横の長さは底辺なので、鈍角三角形の面積は底辺×高さ÷2ということが分かります。
鈍角三角形の面積はなぜ底辺×高さ÷2 part2
もう一つ鈍角三角形の面積が底辺×高さ÷2を導いてみたいと思います。
先程と同じ下の図を使います。

この鈍角三角形の面積は、大きな直角三角形から小さな直角三角形を引いて求めることができます。

青い三角形=(底辺+横)×高さ÷2
ピンクの三角形=横×高さ÷2
となるので、青い三角形からピンクの三角形を引くと、
鈍角三角形の面積=(底辺+横)×高さ÷2-横×高さ÷2
=底辺×高さ÷2
と、なります。
まとめ
三角形の面積の中でも、鋭角三角形や直角三角形の面積はイメージしやすいと思います。
ただ、鈍角三角形はなんだかイメージが付かないという子が多いです。
ちょっとイメージができると、問題にも取り組みやすくなりますし、使わない辺に長さが与えられてもそれにだまさせることもなくなります。
・面積のまとめに戻る



