算数の割り算の等分除を使った余りの意味の考え方

算数の割り算の1つの概念である「等分除」。

6÷2であれば、6を2つに分けると考えるという意味です。

割り切れるときはイメージがしやすいのですが、あまりがでてくると途端にイメージがしにくくなります。

今回の記事では、余りのある割り算は等分除でどう解釈すれば良いのかについて書いてみたいと思います。

 算数の割り算の等分除で考える余りの意味

それでは早速例題を使って考えていきましょう。

(1) \(6\div 2=3\)からみていきましょう。
与えられた式は\(6\div 2\)なので、6を2等分するということですね。
図で書くと下の図のようなイメージになります。

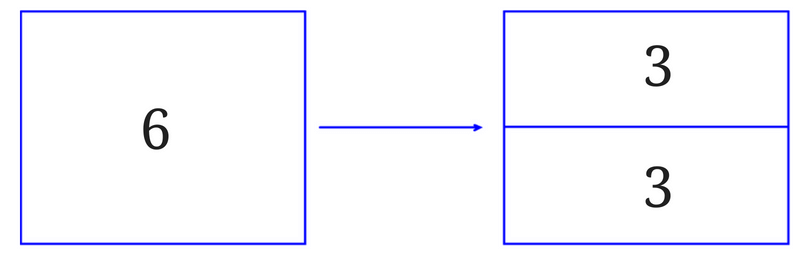
2つに分けた時の1つの塊の中の数が答えという感じになるので答えは3ということになります。

同様に、(2)\(7\div 3=2\cdots 1\)も考えてみましょう。
先ほどの計算では、割り切れたのでなんてことはなかったのですが、今回の計算ではあまりがでます。
与えられた式は、(2)\(7\div 3)なので、等分除の考え方で考えると、7を3等分したときの1つの数が答えとなります。
図で考えると、こんな感じになります。

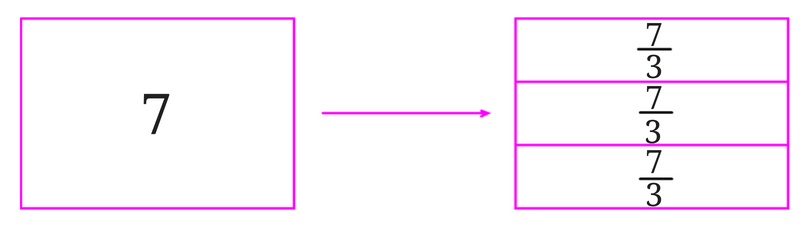
等分除の考え方で\(7\div 3\)を考えてみると、余りがでません。
この時の答えは、\(\frac{7}{3}\)となります。
等分除の考え方では余りのある割り算を考えることができないのでしょうか。

余りのある割り算を等分除で解釈するには一工夫が必要

等分除は割られる数を割る数に等分するという考え方でした。
これが割り切れれば問題ないのですが、割り切れず余りが出てしまうときには、余りを考えることができません。

ここで少し解釈を変えてみます。
\(7\div 3\)を7つの飴を3人の子どもで分けるように考えみます。

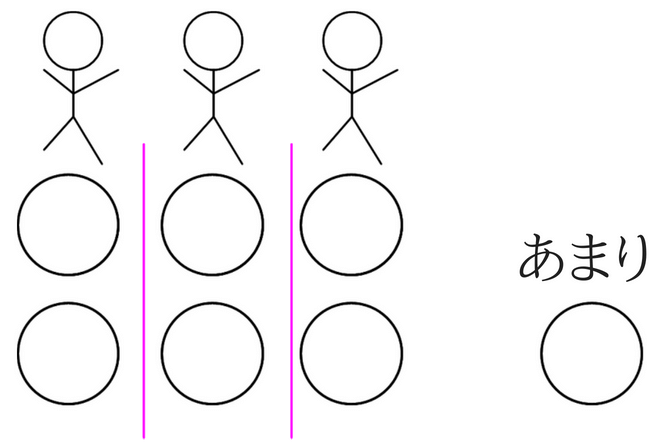
すると、1人が2つで1つ余るということが分かります。
最初の等分除の解釈とこの解釈のどこが違うのかというと、商を整数範囲で考えるかどうかというところです。
最初の等分除の考え方では、整数範囲を超えて考えましたが、その次の考え方では、整数範囲でしか商を考えていません。

等分除を使って余りのある割り算を解釈してみると、整数範囲だけで考えるようにすれば、余りがでたとしてもきちんと解釈できるということが分かります。

小数第一位まで求めたときの余りのある割り算の時は等分除でどう解釈したら良い？

先ほどの(2)の計算問題を小数第一位まで商をだして、余りを求めてみます。
\(7\div 3=2.3\cdots 0.1\)となりました。
この時はどのように考えたらいいのでしょうか。

一の位までを求めるのは先ほどと同じように考えてOKです。
つぎに小数第一位まで計算するということなので、今丸1つを1と考え来ましたが、ここでその丸を10等分したいと思います。

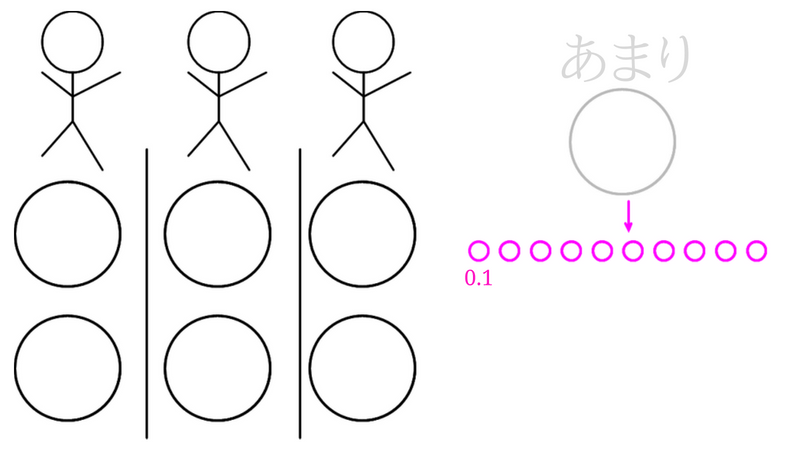
すると今小さな丸が10個できました。
この小さな丸1つは0.1ということです。
この小さな丸10個を3人に分けると、図のようになります。

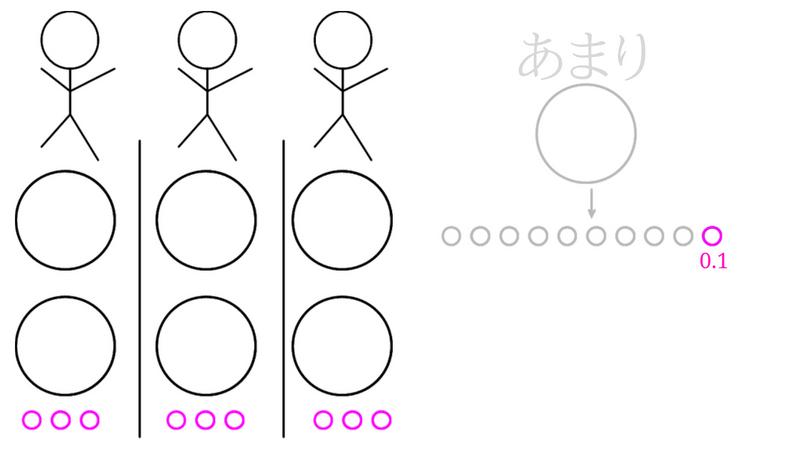
上の図から、1人分は2.3ということが分かりますね。
また、小さな丸が1つ余っているので、あまり0.1ということになります。

まとめ

今回の記事では、余りのある割り算は等分除でどう解釈すれば良いのかについて書いてみました。
等分除や包含除の考え方は割り算の序盤こそでてくるものの、その後はそんなに詳しく扱うことはありません。
割り算で何をしているのか分からないというようなときは、1つ1つきちんと何をしているのか考えてみるといいのではないでしょうか。

もちろん、この考え方が分かるから得をするということはないと思います。
しかし、自分がしている計算が何をしているのか分かると文章題で何をすればいいのか、どのように計算すればいいのかという判断をするときの一助となってくれます。

\(7\div 3=\frac{7}{3}\)のようにあまりを考えずに割ってしまうような場合は、最初にだした例題のように面積として考えるとイメージがしやすいのではないでしょうか。
○のように図化して考えるとどうしても、答えが小数や分数になってしまうときには、その丸をどう分けたらいいのかが分かりにくくなります。

次に\(7\div 3=2\cdots 1\)のように余りがでるときは、1を1つの丸として考えるとイメージがしやすくなります。
一の位まで商を求めて余りまでを出す場合は整数範囲で考えるということを意識することで図示することができます。
飴玉を分けるような場合をイメージできればぴったりだと思います。

小数第一位まで商を求めて余りを出す場合は0.1の位を基準に考えて行くと、小数の商も余りも求めることができます。

【関連記事はこちら】
・割り算の等分除と包含除の意味と違いの教え方とは？