立方体の体積や直方体の体積は、たてと横と高さを掛けることで求めることができます。
なーんだ体積って余裕じゃん!なんて思っていたら登場するのが、「うちのり」という聞きなれない言葉。
大人でもあまり「うちのり」って、耳にしたことがない方のほうが多いのではないかと思います。
聞くとするとマンションの広さなどを表す基準の1つとしてくらいでしょうか。
今回の記事では、体積や容積を求めるときにうちのりを考えないといけない問題について書いてみたいと思います。
内のりってなにー?
「うちのり」って日常生活ではあまり聞くことがない言葉ですよね。
漢字では「内法」と書きます。
小学生にとっては日常ではなかなか耳にしない言葉です。
内のりってどういう意味なのでしょうか。
簡単にいうと内側の寸法のことをいいます。
体積を求める問題でこの内法を求める問題は容積を求める問題となります。
容積ってなにー?
容積というのは、容器にものを入れたときに、その容器に入る量と考えるといいと思います。
容器にいれることができる空間の広さや大きさとも言えます。
例えば冷蔵庫に入る量も容積と言うことになります。
なぜ、容積を求めるときに内法が重要になってくるのかと言うと、実際に入る量が重要になってくるからです。
冷蔵庫にどれくらいの量が入るのかを示したものが全定格内容積です。
これが内法をもとに求めた容積です。
冷蔵室にこんな表示があることが多いと思います。

ちなみにうちの冷蔵庫です。
全定格内容積は\(427L\)あります。
1人暮らしにしてはちょっと大きめですね。
左の真ん中あたりに外形寸法という文字があります。
これは冷蔵庫の外側の長さを測ったものです。
どれくらいの差が出るのか計算してみましょう。
幅\(600mm\)、奥行\(693mm\)、高さ\(1801mm\)となっています。
直方体の体積なので、\(600\times 693\times 1801=748,855,800\)となります。
つまりこの冷蔵庫の体積は、\(748,855,800mm^3\)と言うことですね。
このままでは大きさがよくわからないので、リットルに単位を変換したいと思います。
まずは、立方センチメートルにすると、\(748,855.800cm^3\)となります。
\(1cm^3=1mL\)なので、\(748,855.800mL\)さらにリットルに単位をすると\(748.855800L\)となります。
・小学5年生で習う立体の体積の単位変換はどうするの?立方センチメートルやリットルの関係は?
意外と差がありますね。
これはなぜかというと、食品などが入るところの容積が、全定格内容積にあたるからです。
外側を測って計算をしてもどれだけのものが冷蔵庫に入るのは分からないので、別々に表記してくれています。
・定格内容積、年間消費電力量の測定方法(JIS)
実際に冷蔵庫の内法から容積を求めるのは大変ですが、イメージはつかみやすいではないでしょうか。
小学生の問題では、厚さが\(1cm\)の板で直方体や立方体を作ったものの容積を求めるような問題が多い気がします。
ただ、この問題がよく出るのかというと結構微妙です。
実際には小学生のこの単元でしかでないので、どうにも理解ができない時はスルーしてしまってもそんなに影響はないかもしれません。
もちろん理解することがおすすめではありますよ。
直方体や立方体、またそれらを組み合わせた立体の体積がもとめられるようになっていれば困ることはまずないと思いますよ。
それでは、せっかくなので、容積を求める問題を扱ってみましょう。
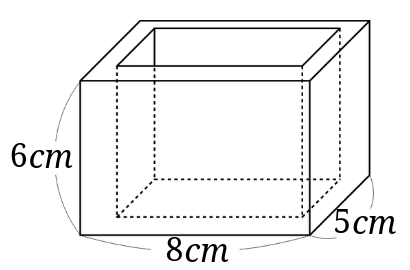
外側の寸法、長さだけ分かっています。
まずはきちんと「うちのり」を求めることが1歩目です。
お子さんがつい3辺をかけてしまうときは、とりあえず体積は3辺をかけてしまえばいいと思っていることもあります。
そんな感じの状態の時は、この「うちのり」をいったん求める問題では掛ければ答えが出せるというものではないので、きちんと体積の求め方を理解しているかの試金石になるかもしれませんね。
「うちのり」を求めると言ってもどこを求めるのかがはっきりしないとどうしていいのか分かりません。
求める辺(?)の長さは図の赤と青とピンクのところです。
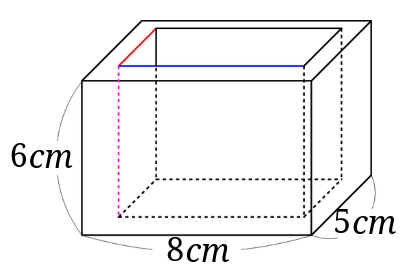 1つずつ求めていくと、「うちのり」は、それぞれ\(3cm\)、\(6cm\)、\(4cm\)となります。
1つずつ求めていくと、「うちのり」は、それぞれ\(3cm\)、\(6cm\)、\(4cm\)となります。
求める容積は、\(3\times 6\times 4=72\)となり、\(72cm^3\)となります。
きちんと内法が求められるとそんなに難しいという感じはないと思います。
容積を求めるためには内法が必要であるということかもしれません。
まとめ
今回の記事では、体積や容積を求めるときにうちのりを考えないといけない問題について書いてみました。
そもそも内法がなんなのかのイメージがないと分かりにくいかもしれません。
実質、算数として何か新しい知識が出てくるというところではありません。
きちんと内法がなんなのか、ということが分かれば後は直方体や立方体の体積を求めると時と違いがあるというものでもありません。
きちんと内法がないを意味するのかだけ分かればOKだと思いますよ。
・小学5年生で習う体積の意味は?かさと何が違うの?容積って?
・かさ・体積・容積のまとめへ戻る




