体積を表す単位には、立方メートル、立方センチメートルなどがあります。
イメージがつかめるのとつかめないのとでは、理解の深さが随分と違ってきます。
できることなら、単位についてもきちんとどういうものか分かっていると理解しやすくなります。
今回の記事では立方メートルの意味について、書いてみたいと思います。
立方メートルって何？どういう意味？
小学生の体積の単位では、\(m^3\)(立方メートル)や\(cm^3\)(立方センチメートル)を使うことが多くあります。
単位の響きだけでいくとどの子もなじみがない、という事はあまりないのではないでしょうか。
しかし、\(m^3\)(立方メートル)や\(cm^3\)(立方センチメートル)の意味がどんな意味なのかという事について考えてみると、様相が変わってきます。
\(m^3\)(立方メートル)って言うのはね･･･
\(cm^3\)(立方センチメートル)って言うのはね･･･
と、説明できるお子さんはそんなに多くありません。
むしろ少数派という感じになると思います。
・小学5年生で習う体積の意味は？かさと何が違うの？
\(m^3\)の意味って何ー？
\(m^3\)の意味って、どんな意味でしょうか。
\(m^3\)だとイメージがしにくいので、\(1m^3\)がどんな大きさかを考えてみましょう。
\(1m^3\)は、1辺が\(1m\)の立方体の体積です。
意味って言ってもこれくらいなものしかありません。
理屈としてはですね。
もちろん正しいのですが、これを覚えたから、何になるのかといわれれば困ってしまいます。
ここで\(1m^3\)の意味を、「1辺が\(1m\)の立方体の体積」だと覚えて欲しいのではありません。
ここで覚えたいのは実際の\(1m^3\)の大きさです。
1辺が\(1m\)の立方体って、実際にイメージしてみるとかなり大きなものです。
ただ立体なのでお子さんにイメージしてもらうのは意外と難しいかもしれません。
そんな時は実際に作ってみましょう。
木材や棒などを上手く使って作るのもいいと思います。
究極ダンボールとガムテープで作ってもOK！
目的は意外と\(1m^3\)が大きいということを感じてもらうことです。
ちょっと見た目が悪くなっても気にせず作っちゃいましょう。
そこまでするのは面倒･･･という場合はおおまかにつかんでもらうだけでもいいと思います。
そんな時はまずは、1辺が\(1m^2\)の正方形を実際に作ってみましょう。
大まかな正方形であれば、メジャーなどがあれば簡単にできると思います。
公園や運動場のような土に実際に書いてみても良いかもしれませんね。
そこから\(1m\)をはかれば、なんとなく\(1m^3\)の大きさはイメージしてもらえるのではないでしょうか。
1m^3は何cm^3になるの？
結論から言ってしまうと、$$1m^3=1000000cm^3$$となります。
このまま覚えても良いのですが、結構覚えられないお子さんが多くいます。
$$1m^3=1000000cm^3$$であることは計算で求めることができます。
まずは、\(1m^3\)が、1辺が\(1m\)の図である事を覚えてもらいましょう。
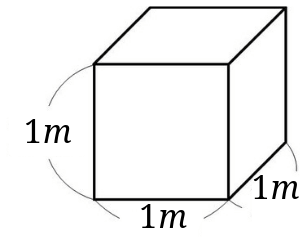この立方体が、何\(cm^3\)であるのかを求めます。
計算をする前に辺の長さをメートルからセンチメートルに単位換算しておきましょう。
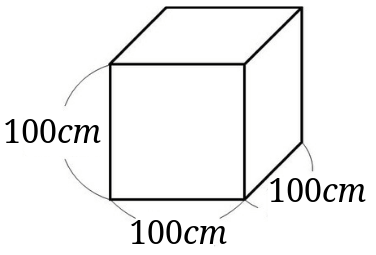辺の長さをメートルからセンチメートルに変更できたらそのまま計算をして体積をだします。
\(100cm\times 100cm\times 100cm=1000000cm^3\)となるので、$$1m^3=1000000cm^3$$となることが分かりました。
ただ、ここまでをしっかり理解できても、いざそれを書くとなると、1と1000000が等しいって変だよね！と思ってしまい、それっぽい答えに変えちゃうお子さんが結構います。
これは単純に1と1000000が同じ大きさを表すということがイメージしづらいことから起こる気がします。
よくある間違いが、\(1m^3=100cm^2\)という誤りです。
\(1m\)が\(100cm\)という数字は子どもたちに自然と受け入れられやすいです。
しかし、\(1m^3=1000000cm^3\)は、受け入れられにくいです。
数字が随分と違いますからね。
受け入れがたい理由の1つが大きさのイメージがしにくいということにあると思います。
実際の\(1m^3\)や\(1cm^3\)の大きさに触れることで、少しでも\(1m^3=1000000cm^3\)が感覚としてもおかしいものではないと飲み込めるといいのではないでしょうか。
実際図で比較してみると・・・
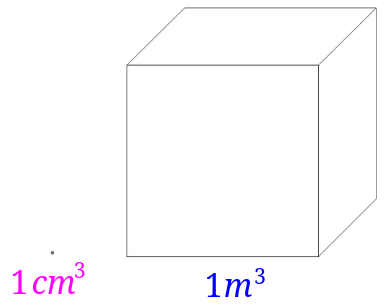随分と大きさが違うんですね。
やはり単位を丸暗記で乗り越えるよりもきちんとイメージをつくってから理解する方がいいのではないでしょうか。
まとめ
今回の記事では立方メートルの意味について、書いてみました。
立方メートルの意味そのものはそんなに難しいものではないと思います。
ただ、この大きさのイメージはきちんとつかんでおくことが、\(1m^3=1000000cm^3\)を数字が違いすぎる！と思うことなく飲み込める土台となるのではないでしょうか。
時間がかかって面倒ではありますが、お子さんが単位を苦手としているときは体感してもらい、大きさを実感できるようにすることが近道なのかもしれませんね。
・直方体や立方体の体積を求める公式は、どうして「たて×横×高さ」なの？
・かさ・体積・容積のまとめへ戻る
