体積の単位と言えば、\(cm^3\)や\(m^3\)を思い浮かべる方が多いのではないでしょうか。
小学生の単位変換のなかでも体積の単位変換は、面積の単位変換と並ぶ単位変換の難しさを誇ります。
特に体積の単位変換は、\(cm^3\)や\(m^3\)の単位変換に加えて、\(L\)や\(mL\)が入ってくるためさらに難しくなります。
今回の記事では体積の単位変化について書いてみたいと思います。
体積の単位変換ができるようになろう
\(cm^3\)、\(m^3\)、\(L\)や\(mL\)の単位変換ができるようになりましょう。
丸暗記ではなくきちんと意味が分かった上で、単位換算ができるようになると、時間が経っても忘れにくくなります。
まずは、\(m^3\)から\(cm^3\)への単位変換をみていきましょう。
体積の単位\(m^3\)から\(cm^3\)に変換する方法
\(1m^3\)って、何\(cm^3\)なの？
まず把握すべきは、\(1m^3\)って、何\(cm^3\)なのかということです。
これはずばり、\(1m^3=1000000cm^3\)です。
もちろん覚えても絶対忘れない！という場合は覚えてしまっても良いのですが、すぐに忘れちゃう、自信を持って答えられないという場合はきちんと理屈まで理解、暗記することがおすすめですよ。
なぜ、\(1m^3=1000000cm^3\)になるのかをみていきましょう。
・小学5年生で習う体積の意味は？かさと何が違うの？
なぜ\(1m^3\)って、\(1000000cm^3\)なの？
最初に\(1cm^3\)の大きさをみてみましょう。
\(1cm^3\)の大きさは1辺が\(1cm\)の立方体です。
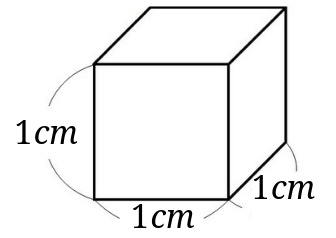
次に\(1m^3\)の大きさみてみましょう。
\(1m^3\)の大きさは、「1辺の大きさが\(1m\)」の立方体です。
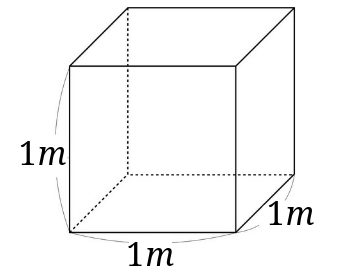
\(1m^3\)が、何\(cm^3\)かを考えていきます。
\(1m^3\)の中に\(1cm^3\)がいくつ入るのかを考えて行きます。
まずは\(1m^3\)の赤の辺に沿って、1辺が\(1cm\)の立方体がいくつ並ぶのかを考えてみましょう。
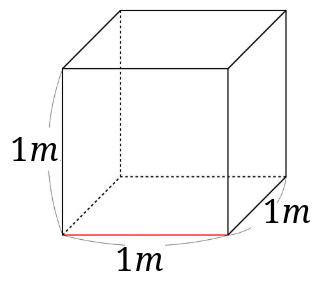赤い辺の長さは\(1m\)、\(1m=100cm\)なので、赤い辺には1辺が\(1cm\)の立方体は100列並べられますよね。
同じように青い辺にも、1辺が\(1cm\)の立方体を並べます。
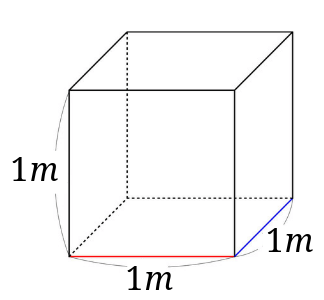
こちらも先程の赤い辺と長さは同じ\(100cm\)なので、赤い辺の時と同様に100列並ぶことが分かります。
たてに100列、横に100列並んだので、底面の正方形には100×100である10000個の立方体を並べることができました。
この1辺が\(1cm\)の立方体を正方形に10000個敷き詰めたものを上に上に重ねていきます。
この1辺が\(1cm\)の立方体を正方形に10000個でできた立体の厚みは、\(1cm\)。
\(1m^3\)の高さは、\(100cm\)なので、100段重ねることができますよね。
ということは、1辺が\(1cm\)の立方体10000個でできた立体が100段積み重なっているので、\(1m^3=1000000cm^3\)ということが分かります。
\(cm^3\)と\(m^3\)と\(mL\)と\(L\)の単位の関係は？
\(1L\)は、何\(mL\)？
\(1L\)は、何\(mL\)なのでしょうか。
\(1L=1000mL\)です。
\(mL\)は意外と日常でよく見かける単位です。
飲み物や液体の調味料など多くのものの量を表すのに使われます。
\(1L=1000mL\)を覚えてもらうには、\(1L\)の牛乳をもとにすると覚えやすいと思います。
実感があると覚えやすいと思いますよ。
ちょっと覚えれば\(cm^3\)と\(m^3\)と\(mL\)と\(L\)の単位換算はできる！！
\(cm^3\)と\(m^3\)の単位換算や\(mL\)と\(L\)の単位変換はイメージをすることがそんなに難しい訳ではないのかもしれません。
しかし、難しいのが\(L\)から\(m^3\)に単位変換するような場合です。
\(1m^3=1000L\)という事実はありますが、覚えていては大変な量になってしまいます。
ここで覚えておくべきは、\(1cm^3=1mL\)です。
数字が同じなので覚えやすいと思います。
これ1つだけで体積の単位換算は対応ができるので、これだけしっかり覚えてもらいましょう。
これをもとに、\(m^3\)から\(L\)に単位を変えることができます。
実際に\(1m^3\)を\(L\)に単位を変換してみます。
\(1cm^3=1mL\)を元に\(1m^3\)が何\(L\)かを求めてみよう
\(L\)や\(m^3\)などの他の単位を、もとに\(1m^3\)を\(L\)にしてみますよ。
まずは\(1m^3\)を\(cm^3\)に単位換算してみます。
\(1m^3=1000000cm^3\)でしたね。
\(1cm^3=1mL\)なので、\(1000000cm^3=1000000mL\)ということが分かります。
\(1000mL=1L\)なので、\(1000000mL=1000L\)となります。
つまり、\(1m^3=1000L\)ということが分かりました。
まとめ
今回の記事では体積の単位変化について書いてみました。
体積の単位変換は、単位変換のなかでも難しいものになると思います。
どうしても長さや面積の単位と混乱、混同してしまうお子さんが多いと思います。
全部の単位の関係を覚えるのは大変です。
大変なだけでなく、混乱すれば間違いになってしまいますし、自信を持って答えを書けないということになってしまいます。
もちろん最低限は覚えないといけませんが、基本となるものを覚えればあとは計算などで出していくのが現実的ではないでしょうか。
・直方体や立方体の体積を求める公式は、どうして「たて×横×高さ」なの？
・かさ・体積・容積のまとめへ戻る
