直方体や立方体の体積を求める応用問題の解き方は？どうやって教えるといいの？

直方体や立方体の体積が求められるようになったら、次は応用問題です。

立方体や直方体の体積を求めるには、「たて×横×高さ」の公式を使えばなんてことなく求めることができました。

しかし、形が複雑になってしまうと、そうとも言っていられません。

立体を切ってみたり、差し引いてみたり…

色々なやり方があります。

今回の記事では直方体や立方体の体積を求める応用問題の考え方のコツについて書いてみたいと思います。

直方体や立方体の体積を求める応用問題の考え方のコツ

立方体や直方体の体積を求めるのはそう難しくありませんでした。
結局のところ3つの辺をかけてしまえば答えが出せましたよね。
・直方体や立方体の体積を求める公式は、どうして「たて×横×高さ」なの？

形が複雑になるとそうもいっていられなくなります。
基本は、直方体や立方体の形に分けることが基本になります。

それでは例題をみていきましょう。

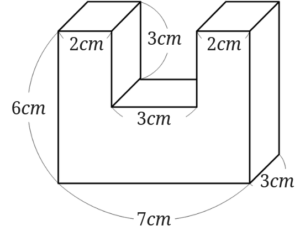
形が複雑な上に、数字がたくさんかいてあります。
立方体や直方体の体積を求める問題では3つしか数字がなかったのと比べると格段に難しくなりますね。
そうはいっても基本は、立方体や直方体の体積の求め方です。
一見複雑に見えるこの立体を立方体や直方体の形に分けてみましょう。
この問題では3つの直方体に分けることができます。

3つの直方体に分けて全体の体積を求める

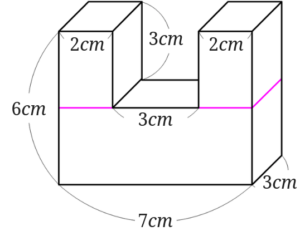
3つの直方体に分けることができれば、１つに1つの直方体の体積は求められますよね。
1つめの直方体の体積を求めましょう。

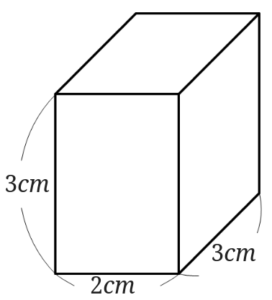
「たて×横×高さ」なので、\(3\times 2\times 3=18\)
２つめの直方体の体積も求めましょう。

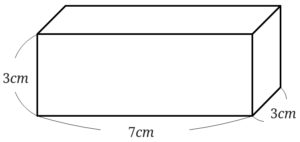
\(3\times 7\times 3=63\)
3つめの直方体も求めていきましょう。

\(3\times 2\times 3=18\)となります。
これら３つの直方体の体積を足すと、元の立体の体積を求めることができます。
\(18+18+63=99\)となるので、この立体の体積は、\(99cm^3\)となります。

そのままの形では、体積を求めることができないので、3つの立体に分けると求められました。
それではもう1つ違う体積の求め方をしてみましょう。

大きな直方体から小さな直方体を差し引く求め方

先ほどは3つの直方体に分けて考えましたが、今回は大きな直方体から中のへこんだ部分の小さな直方体を差し引いて体積を求めてみましょう。

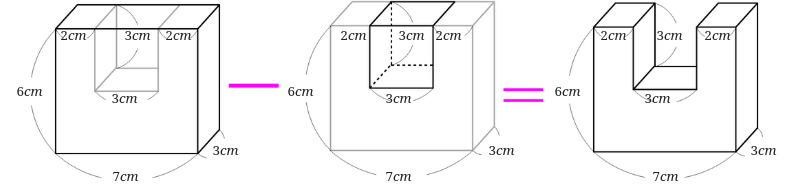
まずは大きな直方体の体積を求めます。

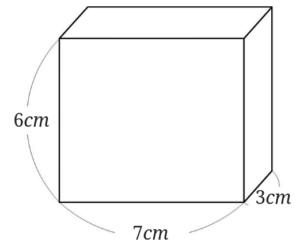
\(7 \times 3\times 6=126\)
大きな直方体の体積は、\(126cm^3\)と分かりました。
次にへこんだ部分の直方体^[1]今回の問題ではたまたま立方体です。9の体積を求めます。

\(3\times 3\times 3=27\)
へこんだ部分の直方体の体積は、\(27cm^3\)と分かりました。
全体の体積から、へこんだ部分の体積を差し引くと、求める体積になるので、\(126-27=99\)となり、求める立体の体積は\(99cm^3\)となりました。

どちらのやり方でもOKです。
好みのやり方でいいと思いますよ。
どちらもできるようになるといいと思いますが、現実的にどちらもというのは、面倒くさがって難しいかもしれません。
そんなときは、問題ごとに解き方を指定してあげると面倒くさい感じは少し減らせるかもしれませんね。

もう1題例題を解いてみましょう。

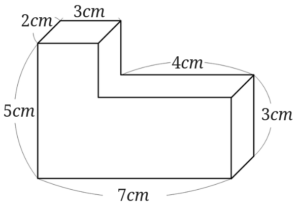
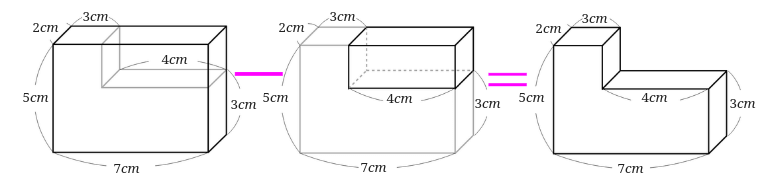
少し形が変わりました。
今回も2通りの解き方でやってみましょう。

2つの直方体に分けて全体の体積を求める

２つの直方体に分けてから全体の体積を求めてみましょう。
まずは、2つの直方体に分けてみます。

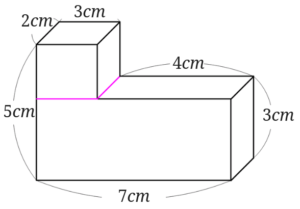
まずは上の小さな直方体の体積を求めてみましょう。
高さにあたる部分が、不明なのでまずは高さを求めましょう。
\(5-3=2\)
これで高さが\(2cm\)ということが分かりました。
上の小さな直方体の体積は、\(2\times 3\times 2=12\)

下の大きな直方体の体積は、\(2\times 7\times 3=42\)
これら2つの体積を合わせると求める体積になるので、\(12+42=54\)
求める体積は、\(54cm^3\)となります。

次に、大きな直方体から、小さな直方体の体積を差し引くやり方で求めてみましょう。

大きな直方体から小さな直方体を差し引く求め方

まずは大きな直方体の体積から求めてみましょう。

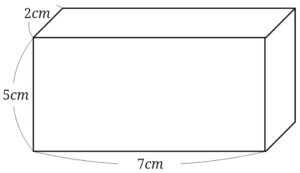
大きな直方体の体積は、\(2\times 7\times 5=70\)となります。
次にへこんだ部分の小さな直方体の体積を求めましょう。

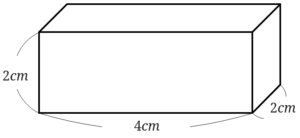
へこんだ部分の小さな直方体の体積は、\(2\times 4\times 2=16\)
全体の大きな直方体から、へこんだ部分の直方体の差を取ると、\(70-16=54\)となり、求める立体の体積は、\(54cm^3\)となります。

まずはお子さんが解きやすいやり方で解けるようになるといいですね。

練習問題

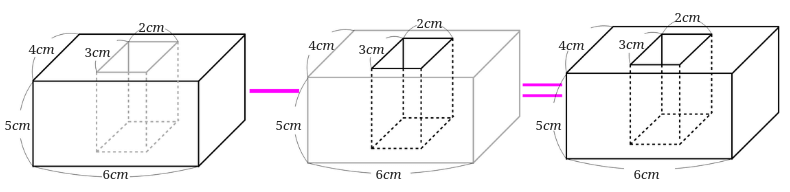
1、下のような形の体積を求めましょう。

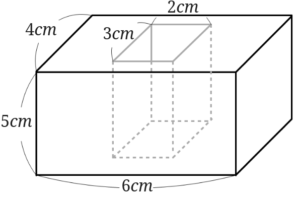
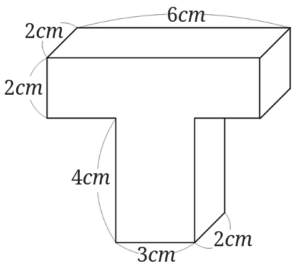
2、下のような形の体積を求めましょう。

解答と解説

1の解説

全体の直方体から、くりぬいてある部分の体積を差し引きます。$$4\times 6\times 5- 3\times 2\times 5=90$$求める立体の体積は\(90cm^3\)となります。

2の解説

計算の手間から考えると、2つの直方体に分けて考えるとやりやすいと思います。
上側と下側に分けてみましょう。

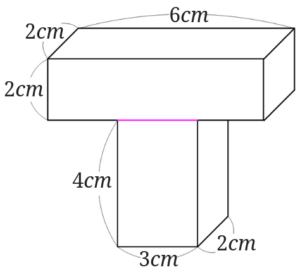
まずは上の直方体の体積を求めます。
\(2\times 6\times 2=24\)
下側の体積も求めてみます。
\(2\times 3\times 4=24\)
これら2つの直方体を足すと求める立体の体積になります。
\(24+24=48\)となり、求める立体の体積は\(48cm^3\)となります。

まとめ

今回の記事では、直方体や立方体の体積を求める応用問題の考え方のコツについて、書いてみました。

複雑な形の立体となるとそのまま公式にいれて解くということが、できなくなるので難しくなります。
求められる立体の形にもとに立体を分けたり、全体を求めて、一部を差し引くという形で体積を求めるということも可能になります。
どうにもならない時はまずは、一緒に2つに分けてみてもいいかもしれませんね。
・かさ・体積・容積のまとめへ戻る