体積が求められるようになると1番最初に扱う立体が、立方体や直方体です。
立方体の体積を求める公式は、「一辺×一辺×一辺」。
直方体の体積を求める公式は、「たて×横×高さ」です。
覚えてしまえば、簡単に体積が求められますが、ちょっと理解すると、立方体や直方体の体積を求める公式は、立方体や直方体の体積を求める常識という感じになります。
今回の記事では、立方体や直方体の求めるときに使う公式の意味について書いてみたいと思います。
体積を求める公式の理解は単位の「立方メートル」の意味から!
まずは「立方メートル」の意味から考えてみましょう。
「立方メートル」を記号で書くと、\(m^3\)と表記します。
\(m^3\)の3の読み方って他にもありますよね。
この場合は「3乗」と読みます。
中学生になると習う累乗の考え方です。
\(m^3\)の意味は、\(m\)の3乗なので\(m\times m\times m\)ということです。
\(m\)を3回かかけるという意味になります。
つまり、\(m^3\)は、\(m\times m\times m\)[1]メートル×メートル×メートルという意味になります。
\(m^3\)という体積の単位から長さ(メートル)を3回掛けるという意味になります。
同じように「立方センチメートル」も「立方メートル」同じように解釈できます。
「立方センチメートル」を記号で書くと、\(cm^3\)と表します。
\(cm^3\)の意味は、\(cm\)を3回かけるという意味になります。
つまり\(cm^3\)は、\(cm\times cm\times cm\)[2]センチメートル×センチメートル×センチメートルという意味になり、単位がセンチメートルの長さを3回かけたということになります。
お子さんに教える際には、先に累乗の数の書き方を教えておくとスムーズに理解してくれます。
書き方だけなので、拒否反応がでることは少ないと思います。
・直方体や立方体の体積を求める公式は、どうして「たて×横×高さ」なの?
それでは例題を解いてみましょう。
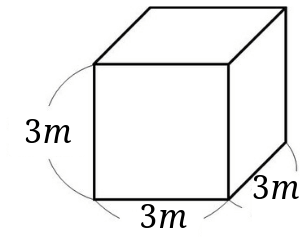
一辺が\(3m\)の立方体の体積を求める問題です。
単位に指定がないので、「立方メートル(\(m^3\))」、「立方センチメートル(\(cm^3\))」の両方で求めてみましょう。[3]小学校のテストなどの場合は両方ではなく1つだけで大丈夫だと思います。今回は練習ということで、\(cm^3\)と\(m^3\)の両方の場合を求めます。
何\(m^3\)なのかを求めてみます。
立方体の体積が何\(m^3\)なのかを求める方法
聞かれている単位が\(m^3\)なので、縦、横、高さ[4] … Continue readingの単位を\(m\)にして、掛けるといいということです。
一辺が\(3m\)の立方体なので、単位は特に直す必要はありません。
縦、横、高さを掛けて\(3\times 3\times 3=27\)となります。
この立方体の体積は\(27m^3\)と言うことが分かりました。
単位を全く変換することなくできたので、やりやすいですね。
次に、何\(cm^3\)なのかを求めてみます。
立方体の体積が何\(cm^3\)なのかを求める方法
何\(cm^3\)なのかを聞かれたと言うことは、\(cm\)を3回掛けると言うことが分かります。
この立方体の体積が何\(cm^3\)なのかを求めるには、1辺の長さの単位が\(m\)になっているので、\(m\)から\(cm\)に変えるところからスタートです。
\(3m\)は、\(300cm\)なので、この立方体は一辺が\(300cm\)の立方体ということが分かります。
この立方体の体積を求めると、\(300\times 300\times 300=27000000\)となるので、この立方体の体積は\(27000000cm^3\)となります。
特に単位指定がないので、答えは\(27m^3\)でも\(27000000cm^3\)のどちらでもOKです。
問題文で何\(m^3\)とあれば\(m^3\)で、何\(cm^3\)とあれば\(cm^3\)で答えてくださいね。
・小学5年生で習う立体の体積の単位変換はどうするの?立方センチメートルやリットルの関係は?
もう1題例題を解いてみましょう。
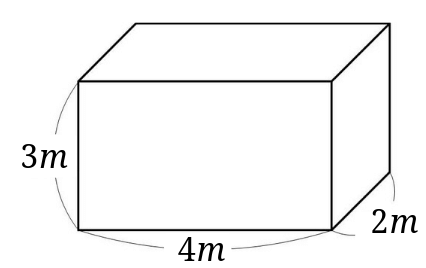
今回の例題も単位指定がないので、「立方メートル(\(m^3\))」、「立方センチメートル(\(cm^3\))」の両方で求めてみましょう。
まずは、何\(m^3\)かを求めます。
直方体の体積が何\(m^3\)なのかを求める方法
直方体の体積は、たて×横×高さで求めることができ、単位は\(m^3\)です。
与えられた直方体の辺の長さはすべてメートルになっているので、そのまま、縦、横、高さを掛ければいいということになります。
\(2\times 4\times 3=24\)となり、\(24m^3\)と言うことが分かりました。
次に何\(cm^3\)なのか求めてみましょう。
直方体の体積が何\(cm^3\)なのかを求める方法
求める単位が\(cm^3\)なので、\(cm\)を3回掛けるという意味でした。
直方体の各辺の単位はメートル。
まずは各辺の長さをメートルからセンチメートルに単位換算したいと思います。
たての長さが\(2m\)、横の長さが\(4m\)、高さが\(3m\)をセンチメートルに単位変換すると、それぞれ、\(200cm\)、\(400cm\)、\(300cm\)になります。
求める直方体の体積は、\(200\times 400\times 300=24000000\)となるので、\(24000000cm^3\)となります。
練習問題
1、下のような形の体積を求めましょう。
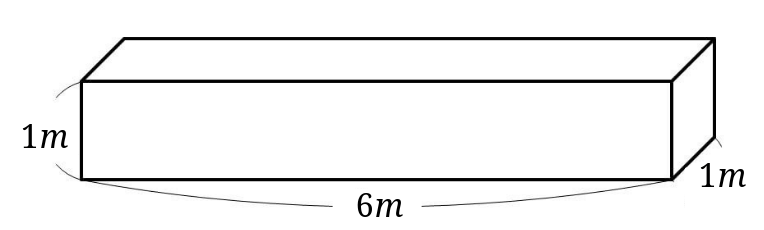
2、下のような形の体積を求めましょう。
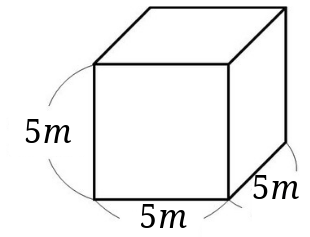
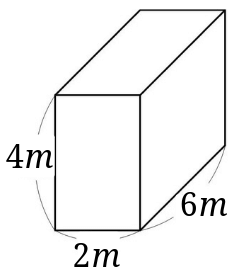
3、下のような形の体積を求めましょう。
解答と解説
「立方メートル(\(m^3\))」と「立方センチメートル(\(cm^3\))」の両方で体積を求めてみましょう。
1の解説
体積は何\(m^3\)?
\(1\times 6\times 1=6\)となるので、求める直方体の体積は、\(6m^3\)となります。
体積は何\(cm^3\)?
まずは各辺の単位をメートルからセンチメートルにします。
\(100\times 600\times 100=6000000cm^3\)となるので、求める直方体の体積は\(6000000cm^3\)となります。
2の解説
体積は何\(m^3\)?
\(5\times 5\times 5=125\)
求める立方体の体積は\(125m^3\)となります。
体積は何\(cm^3\)?
各辺の単位をメートルからセンチメートルにして計算します。
\(500\times 500\times 500=125000000\)
求める立方体の体積は、\(125000000cm^3\)となります。
3の解説
体積は何\(m^3\)?
\(2\times 6\times 4=48\)
求める直方体の体積は、\(48m^3\)となります。
体積は何\(cm^3\)?
各辺の単位を\(m\)から\(cm\)にして計算していきます。
\(200\times 600\times 400=48000000cm^3\)
求める直方体の体積は、\(48000000cm^3\)となります。
まとめ
今回の記事では、立方体や直方体の求めるときに使う公式の意味について書いてみました。
公式の意味はなくても、問題そのものを解くことはできます。
しかし、少しイメージができるだけで単位を合わせたり、単位が入り混じった計算でも、単位を揃えるのを忘れずに当たり前にすることができるようになります。
公式の丸暗記ではなく少なくとも、自身の計算が何をしているのかのイメージができるといいのではないでしょうか。
今回の体積を求める問題では、立方メートルと立方センチメートルの両方で求めてみました。
もともと単位がメートルの問題なので、立方センチメートルを求める時は、始めにメートルをセンチメートルにするところから始めましたが、立方メートルを求めてから単位を立方センチメートルになおすことでもできます。
どちらでもできるようにしておくといいと思いますよ。
・かさ・体積・容積のまとめへ戻る




