今回の記事では速さの単元の時間の求め方を扱っていきます。
時間を求めるには割り算をつかうことが多いのですが、1番の問題点は割り算がイメージしにくいこと。
ここがクリアできないとどうしても公式を丸暗記することになりがちです。
暗記しなくても、どうすれば時間を求められるのかについて書いています。
単位の変換をすることなく計算できる問題だけを扱っていきます。
それではみていきましょう。
速さや距離の単位換算を伴わない時間の求め方
それでは例題を使って考えていきましょう。
1時間に\(40km\)進むので$$200\div 40=5$$となり、時速\(40km\)のトラックで\(200km\)を走るのには5時間かかるということになります。
式を見ればそんなに難しくないのですが、この式の意味するところが分かると、この式を立てることが当たり前に見えてきます。
この時の考え方は割り算の包含除をイメージしてもらえると分かりやすくなります。
割られる数の中にいくつ割る数が入っているのかという考え方です。
\(200\div 40=5\)という式は200の中に40が5つ入っているというイメージになります。
それではなぜ、答えが5時間ということになるのでしょうか。
これは、時速\(40km\)が1時間に\(40km\)進むということから考えます。
\(200km\)には40のかたまりが5つ入っています。
と、いうことは\(200=40+40+40+40+40\)とみることができます。
\(40km\)ごとに1時間かかるので、5時間かかるということが分かります。
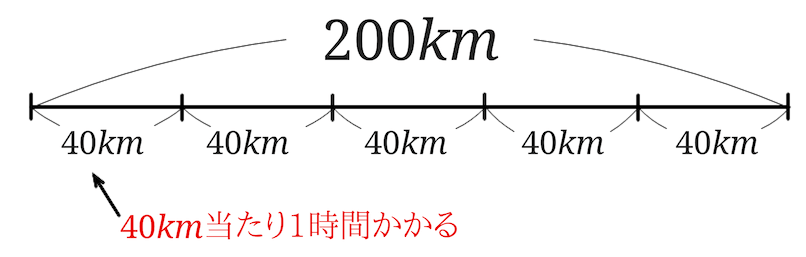
割り算の考え方と速さの表し方がポイントになります。
基礎的だけどなんとなく流されがちな点なので、きちんと理解させておくことが後々ものをいいますよ。
もう1題例題をみてみましょう。
分速\(200m\)は1分間に\(200m\)歩くという意味です。
と、言うことは\(800m\)の中に\(200m\)のかたまりがいくつ入っているか分かればかかる時間も分かるということになります。$$800m\div 200=4$$と、なるので4分が答えになります。
速さの単元の式としてはこのようになります。
ちょっと違う考え方をしてみると、こんな感じの式でもOKだと思います。
\(800m=200m+200m+200m+200m\)となるので答えは4分となるという考え方でも答えは出せますね。
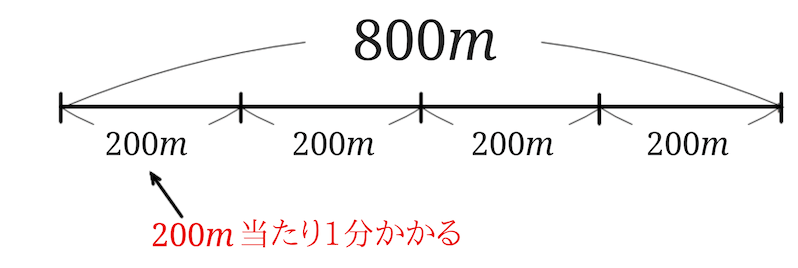
そもそも200のかたまりが800の中にいくつあるかが分かれば答えにたどり着けるから、公式を使わずに、直接200のかたまりをつくっちゃうということでも答えはだせますね。
このやり方の欠点は、答えが整数になるときにしか使えないところです。
答えが小数や分数になってしまうときは、この方法だけでは答えまでいきつけません。
もう一つの問題点は、小学校のテストでこの解き方をするとおそらく不正解とされてしまうと思います。
小学校のテストで必要とされる式が微妙ですし…
ただ、答えを出す過程をお子さんに見せるにはいい方法ではないでしょうか。
割り算の意味と合わせてやってみると、なぜ割り算をすることで時間が求められるのかが見えやすくなると思います。
・速さや距離の単位変換などが必要な時の時間の求め方はこちら
時間を求める公式は割り算の理解がポイント
速さの三公式を見てみると、
- 道のり(距離)=速さ×時間
- 速さ=道のり(距離)÷時間
- 時間=道のり(距離)÷速さ
と、道のり(距離)を求める時のみ掛け算で、残りの速さや時間を求める時は割り算になっています。
ここのところが結構くせ者です。
大抵のお子さんは掛け算はイメージしやすいのですが、割り算ってイメージがしづらいんですね。
そのせいかとりあえず公式を暗記してそこに数字をあてはめて解こう!となるわけです。
つまり、割り算を使っている「速さ=道のり(距離)÷時間」「時間=道のり(距離)÷速さ」この2つの公式の攻略が鍵になります。
ここのイメージがわけば公式に頼らなくても、見れば分かったり、ちょっと考えれば答えが出せるようになります。
練習問題
1、時速\(45km\)で走る電車があります。この電車が\(135km\)走るときにかかる時間は何時間ですか。
2、家から図書館までの道のりは\(2100m\)です。分速\(70m\)で家から図書館まで歩くと何分かかりますか。
3、秒速\(25m\)で走る車が、\(3500m\)進むのに何秒かかりますか。
4、時速\(20km\)で走る自転車が、\(90km\)進むのに何時間かかりますか。
5、分速\(60m\)で歩くとき、\(30m\)進むのに何分かかりますか。
解答と解説
1の解説
時速\(45km\)は1時間に\(45km\)進むということなので、\(135km\)の中に\(45km\)がいくつあるか分かれば時間が求められます。$$135\div 45=3$$となるので、3時間ということになります。
\(45km\)ごとに1時間かかるイメージがわけばいいと思います。
2の解説
分速\(70m\)は、1分間に\(70m\)進むという意味なので、\(2100m\)の中に\(70m\)がいくつあるか分かれば時間が求められます。$$2100\div 70=30$$となるので、30分ということになります。
3の解説
秒速\(25m\)は1秒間に\(25m\)進むという意味です。
\(3500m\)は\(25m\)のいくつ分でできているか分かれば、時間が求められます。$$3500m\div 25=140$$となるので、140秒ということになります。
4の解説
時速\(20km\)は1時間に\(20km\)進むという意味です。
\(90km\)がいくつの\(20km\)のかたまりからなっているのかが分かれば時間が求められます。$$90\div 20=4.5$$となるので、4.5時間ということになります。
5の解説
分速\(60m\)は1分間に\(60m\)進むという意味なので、\(30m\)の中に\(60m\)のかたまりがあるのかが分かれば時間が求められます。$$30\div 60=0.5$$ということで、0.5分と分かりました。
小数や分数になるとイメージが急にわきにくくなると思います。
特に5番はイメージするのが難しかったかもしれませんね。
実際に解くときには考えませんが、もう少し細かく単位を見てみるとイメージがつくようになります。
分速\(60m\)は1分間に\(60m\)進むという意味でした。
すこーしこれを拡張して考えると、0.1分間に\(6m\)進むという風に見ることもできますよね。
\(30m\)の中に\(6m\)のかたまりがいくつあるのかを考えます。$$30\div 6=5$$となるので、\(30m\)には\(6m\)のかたまりが5つあるということになります。
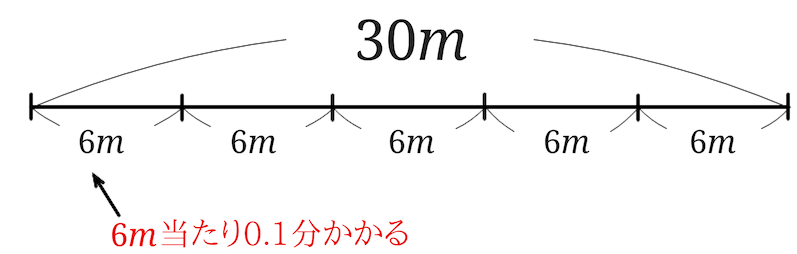
\(6m\)ごとに0.1分かかるので、\(6m\)のかたまりが5つあるということは、$$0.1\times 5$$とすることで、時間が求められることになります。
つまり0.5分ということになりますよね。
まとめ
今回の記事は速さの単元の時間の求め方をについてでした。
速さの表し方と割り算の概念がしっかり分かっていれば、解くことは難しくありません。
分からない場合は、速さの表し方か割り算の概念がよく分かっていないことがその原因のほとんどです。
時間の求め方が苦手というときでも、割り算の概念や速さの表し方を習得する方が速さができるようになる近道になる気がします。




