速さの公式に頼らない道のりの求め方ができるようになろう。

速さの単元で、でてくる道のりの求め方。
道のり=速さ×時間の公式に数字を入れれば簡単に出せるのですが、結構、この公式を上手く使えないお子さんが多いものです。
速さの単元における公式は3つ。
たった3つなのですが、覚えられなかったり、どう使えばいいのか分からなかったり･･･
特に単元が終わるとシュッと忘れてしまうお子さんが多いです。

今回の記事では、そんなことにならないように、普通に見れば解ける道のりの求め方をご紹介していきたいと思います。

小学校の速さの単元の道のりの求め方

道のりの求め方を見る前に、速さの基本を押さえておきましょう。
速さの単位の意味が分かればこれ以降も理解できると思いますが、ちょっと知識があやしそうな場合は1度復習してみてください。
速さの単元の要になります。
・速さの単位、時速、分速、秒速の意味はこちら

速さの単位の意味をおさえたら、早速道のりを求めていきましょう。

「道のり＝速さ×時間」という公式に突っ込みたくなるところですが、意味からしっかり考えてみましょう。
「時速」の意味は「1時間に進む距離」でした。
つまり、時速\(20km\)は、1時間に\(20km\)進むという意味ですね。
1時間ごとに\(20km\)進むということなので、\(20km\)を2倍すれば移動した距離が出せるということになります。$$20km\times 2=40km$$となり、進んだ道のりは\(40km\)になります。

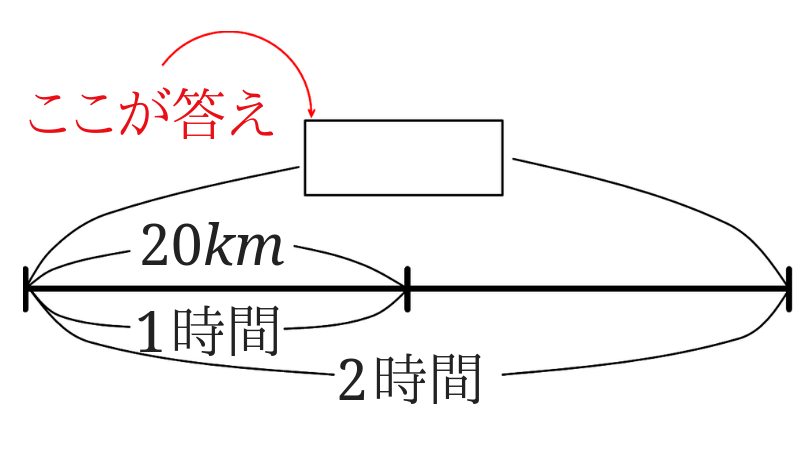
時速の意味をきちんと理解することがポイントです。

もう1問してみましょう。

「分速」の意味は、「1分間に進む距離」ということです。
つまり、分速\(150m\)は、1分間に\(150m\)進むという意味ですね。
1分ごとに\(150m\)進むということなので、\(150m\)を12倍すれば移動距離が出せるということになります。$$150\times 12=1800m$$となり、進んだ距離は\(1800m\)ということになります。

どうでしょうか？
「時速」や「分速」の意味がきちんと分かれば、簡単に解くことが出来そうですね！

次にちょっと時間がイメージしにくい場合をやってみましょう。

時間が小数になってしまいました。
とは言っても、やり方は変わらないので安心してくださいね。

「秒速」の意味は、「1秒間に進む距離」でした。
つまり、秒速\(30m\)は、1秒間に\(30m\)進むという意味です。
1分ごとに\(30m\)進むということなので、\(30m\)を3.5倍します。$$30m\times 3.5=105m$$となるので、進んだ道のりは\(105m\)ということになります。

時間が小数になったのでちょっと分かりにくくなった感じがします。
しかし、小数になったからといってやり方は変わりません。
整数の時と同じようにすればいいということになります。

練習問題

1、秒速\(5m\)で、30秒走りました。何\(m\)進みましたか。

2、時速\(40km\)のバスに2時間乗りました。何\(km\)進みましたか。

3、自転車に乗って分速\(300m\)で7分進みました。何\(m\)進みましたか。

4、分速\(30m\)で20分歩いた後、分速\(50m\)で3分歩きました。
合わせて何\(m\)歩きましたか。

5、時速\(50km\)で車を2時間運転し、その後分速\(0.2km\)で15分走りました。
合わせて何\(km\)移動しましたか。

解答と解説

1の解説

1秒間に\(5m\)進むので30倍すれば走った距離になります。
\(5m\times 30=150m\)

2の解説

1時間に\(40km\)進むので2倍すればバスが進んだ道のりになります。
\(40km\times 2=80km\)

3の解説

1分間に\(300m\)進むので、7倍すれば自転車で進んだ道のりが出せます。
\(300m\times 7=2100m\)

4の解説

1分間に\(30m\)進むので、20倍すれば歩いた距離になります。
\(30m\times 20=600m\)

5の解説

この問題は車で移動した距離と、その後に走った距離を別々に出す必要があります。
ちょっと手間は増えますが1つずつきちんと出せば答えは出せますよ。

まずは車での移動距離を出します。
1時間に\(50km\)進むので、これを2倍します。
\(50km\times 2=100km\)

次に走った距離を出します。
1分間に\(0.2km\)進むので、これを15倍します。
\(0.2km\times 15=3km\)

車での移動距離と走った距離を合計すれば答えとなります。
\(100km+3km=103km\)

まとめ

今回の記事では道のりや距離の求め方をしました。
やはり速さの問題を解くうえで基本となるのは「時速」、「分速」、「秒速」の意味となります。
この3つを理解することが速さの単元を攻略する近道となります。
全部公式にしちゃうと無限に公式が増えてしまいますからね。

速さの三公式^[1] … Continue readingを覚えると簡単に解くことができます。
・きはじ（みはじ）を使った速さの3公式の覚え方はこちら

しかし単純に公式を覚えて解こうとしても、意外とそううまくいかないんですよね…
理屈の上では公式を覚えれば簡単に解けるはずなのですが…
もちろんそれでも解けるよ！という場合は公式を使ってもいいのかもしれませんが、後々の応用を考えるときちんと理解するのがおすすめですよ。

小学生6年生の算数の速さのまとめに戻る