速さの三公式のうち、時間と速さを求める公式は割り算になっています。
道のりを求めるのはそこまで苦戦しませんが、時間と速さに関してはうーん…となってしまうお子さんも多いです。
今回の記事では速さの求め方を扱っていきたいと思います。
速さの求め方を時速、分速、秒速ごとに丁寧に解説します!
速さを求めるには、距離÷時間をすればすぐに求めることができるのですが、速さの単元を終えてしばらく時間が経つとできなくなってしまいがち。
場合によっては学校で速さを習っている最中にすでに分からなくなっていることも多いです。
せっかくであればきちんと解けるようにしておきたいですよね。
速さの求め方を理解するには、速さの表し方と割り算の考え方が欠かせません。
速さの表し方に自信がないなぁというときは下の記事を見てくださいね。
・速さの意味を理解して時速や分速と秒速の表し方をマスターしよう!
速さの意味がしっかり理解できていれば、速さの求め方も理解しやすくなります。
逆によく分からなければあまり理解することが難しくなります。
それでは例題をみながら、速さの求め方について理解していきましょう。
時速の求め方とは?
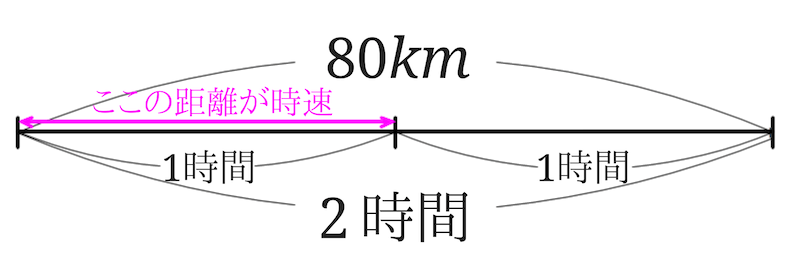
時速を求める問題です。
時速が何を意味するのかきちんと分かっていることが大事です。
時速とは、1時間に進む道のり(距離)のことを意味しています。
つまり、1時間にどれだけ進んだのかが分かればいいと言うことになります。
2時間で\(80km\)進んだということは、$$80km\div 2$$をすることで、速さを求めることができます。
計算すると\(40km\)になるので、答えは時速\(40km\)となります。
今回の例題では$$80\div 2$$という式を立てましたが、この式のイメージをつかむには割り算の意味を理解しておくことが最短となります。
基礎的過ぎて面倒に感じるかもしれませんがしっかりつかんでおくといいですよ。
ちなみに\(80\div 2\)の意味は、\(80km\)を2等分するという等分除で考えると理解できますよ。
分速を求める方法
次の例題を見てみましょう。
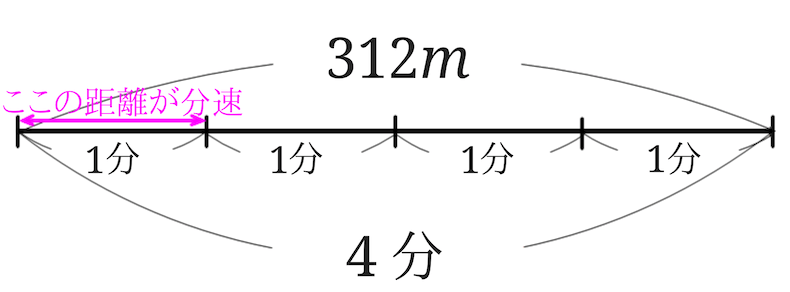
今度は分速を求める問題です。
分速とは、1分間に進む道のり(距離)のことを意味しています。
分速を答えるので、1分間にどれだけ進んだのかを求められればいいということになります。
4分間で\(312m\)進んだということは、$$312m\div 4$$をすることで、1分間に歩いた距離を求めることができます。
計算してみると\(78m\)となります。
答えは分速\(78m\)です。
秒速の求め方を解説
次の例題を見てみましょう。
<例題>
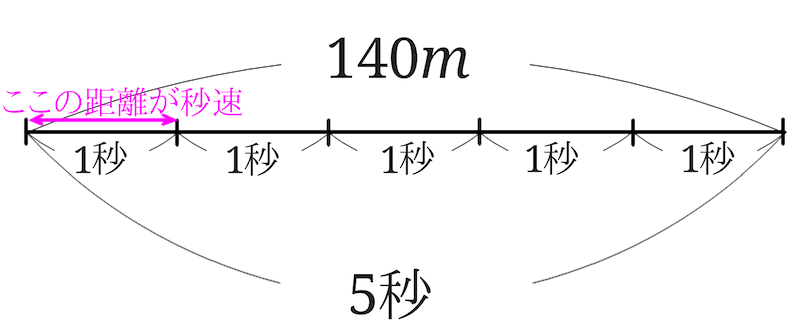
5秒間で\(140m)進む自動車があります。この自動車の速さは、秒速何\(m\)ですか。
今度は秒速を求める問題です。
秒速を答えるので、1秒間に進んだ道のり(距離)が分かればいいということになります。
5秒間で\(140m\)進んだということは$$140\div 5$$をすれば、1秒間に自動車が進んだ道のり(距離)を求めることができます。
計算すると\(28m\)となるので、答えは秒速\(28m\)ということになります。
「時速」、「分速」、「秒速」と1題ずつみてみましたが、考え方はみんな一緒でしたね。
まずはこの「時速」、「分速」、「秒速」の3つの意味をしっかり理解し覚えましょう。
計算や文章題はそれからですね。
練習問題
1、\(600m\)を5分で走りました。分速何\(m\)で走りましたか。
2、家から図書館までの道のりは\(2700m\)あります。自転車で行くと15分かかりました。自転車の速さは分速何\(m\)ですか。
3、\(150km\)の道のりを自動車で行くと5時間かかりました。自動車の速さは時速何\(km\)ですか。
4、よしこさんは\(4800m\)歩くのに、1時間20分かかりました。
①1時間20分は何分ですか。
②よしこさんの歩いた速さは分速何\(m\)ですか。
5、たろう君は\(4620m\)家から離れた公園に歩いて行くのに1時間10分かかりました。たろう君の歩く速さは分速何\(m\)ですか。
解答と解説
1の解説
分速を求めるには、1分間に進む道のり(距離)を出せばいいので$$600\div 5=120$$となります。
求める答えは\(120m\)ということになります。
2の解説
\(2700m\)の道のりに15分かかっているので、1分あたりに進む距離は$$2700\div 15=180$$となるので、\(180m\)ということになります。
答えは分速\(180m\)ということになります。
3の解説
今度は時速を求める問題です。
時速は1時間に進む距離なので、時速を求めるには$$150\div 5$$をすればいいことになります。
計算すると30となるので、時速\(30km\)ということになります。
4の解説
①の解説
時間と分が混ざっているので分だけにします。
1時間=60分なので、1時間20分は80分ということになります。
②の解説
①からよしこさんが歩いた時間は80分です。
1分間に進んだ道のりを求めればいいので、$$4800\div 80$$を計算すればいいということになります。
計算すると60となるので、答えは分速\(80m\)となります。
⑤の解説
4、では親切な誘導がついていたのでやりやすかったのですが今度の問いには誘導がありません。
まず見るべきは求めるものです。
この問いでは分速何\(m\)かを聞かれています。
距離をみると単位が\(m\)なのでそのままでよさそうです。
しかし、時間を見ると、1時間と10分というように時間と分が混ざっています。
分速を求めるので時間は分だけの形にすると70分となります。
あとは\(4620\div 70\)をすればOKです。
計算すると66となります。
答えは分速\(66m\)となります。
4と5はちょっと難しかったかもしれませんね。
単位を見ることなく適当に計算すると、間違ってしまうので単位をよく見る癖をつけておくといいですね。
まとめ
今回の記事では、速さの求め方を時速、分速、秒速それぞれについて解説しました。
速さの意味が分かって入れば、求め方そのものはそんなにややこしいものではありません。
しかし、割り算の概念や速さの表し方の知識が曖昧だとなんだかよくわからない!ということになってしまいます。
まずは割り算の考え方と速さの表し方は余裕で分かるというところまでさせておくのがいいかもしれませんね。




