時速から分速のような時間の単位だけでなくkmからmの距離の単位まで速さの単位変換ができるようになろう！

速さの単位変換って慣れると簡単だけど慣れるまでは結構難しいもの。
単位変換に慣れる前にやり方をとりあえず丸暗記しちゃえ！ってなってしまうことも多いものです。
教える側もやり方を丸暗記させた方が楽ということもあり、「時速を分速に変えるときには…」、「秒速を時速に変えるときには…」という教え方になりがちです。
もちろんこのやり方が絶対に悪いというわけではありませんが、私は覚えることが増えるのであまり好きではありません。
単位変換をする必要があるものは速さに限らないので、色々な単位変換を丸暗記していくのは後々の混乱に繋がりやすいものです。

この記事では、単位変換の丸暗記をすることなく、速さの基本的な見方をもとに単位変換ができるやり方について書いていきたいと思います。

時速から分速のような時間の単位だけでなくkmからmの距離の単位まで速さの単位変換をマスターしよう。

時速○$km$を分速△$m$に直してみよう

時速30$km$は分速何$m$かを考えてみましょう。

時速や分速の意味は大丈夫ですよね。
時速とは1時間に進む距離のことで、分速とは1分間に進む距離のことです。

まずは時速$30km$を分速になおします。
時速$30km$は1時間、つまり、60分間に$30km$進むという距離です。
30を60で割ることで1分間に進む距離にすることできます。
つまり、60で割ることで分速にすることができるということです。$$30\div 60=0.5$$ということで、時速$30km$は分速$0.5km$ということが分かりました。
今回は分速〇$m$にすることが目的なので$km$を$m$に直します。
$0.5km=500m$なので、時速$30km$は分速$500m$ということになります。

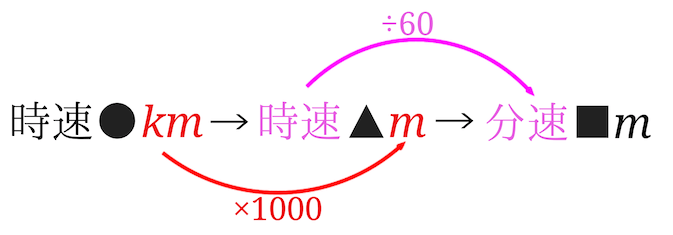
時速〇$km$→分速△$km$→分速□$m$と単位変換しました。
その単位を変えた過程を図にすると下のようになります。

もちろん、時速●$km$→時速▲$m$→分速■$m$という流れでもOKです。
こちらの流れで時速$30km$を分速■$m$に直してみます。

$km$を$m$に変えると時速$30000m$となります。
$30000m$は60分間に進む距離なので、60で割ると分速に直すことができます。$$30000\div 60=500$$となるので、時速$30km$は分速$500m$ということになります。

もちろん、どちらのやり方でやってもOKです。
計算が楽になりそうな方法でするといいですね。

秒速○$m$を分速△$m$に単位変換してみよう

秒速350$m$を分速何$km$かを考えます。

先ほどと同じように2パターンのやり方でやってみます。

秒速○$m$→分速△$m$→分速□$km$の順に単位変換

350$m$は1秒間に進む距離なので、60倍をすることで分速になおすことができます。$$350\times 60=21000$$となるので、分速21000$m$ということになります。
あとは$m$を$km$になおしてあげると、分速21$km$となりました。

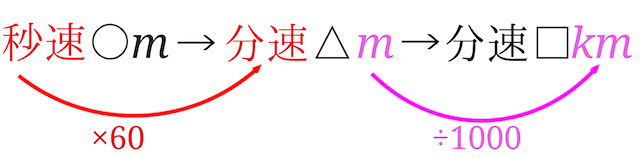
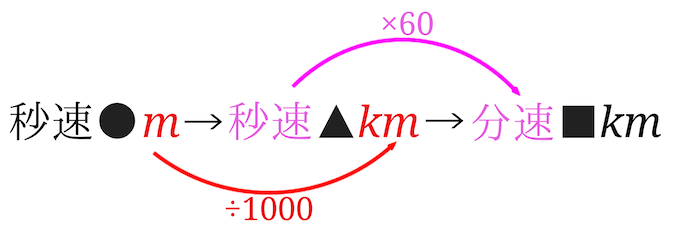
秒速●$m$→秒速▲$km$→分速■$km$の順に単位変換

秒速350$m$の$m$を$km$になおすと、秒速$0.35km$となります。
$0.35km$は1秒間に進む距離なので、60倍すると分速に直すことができます。$$0.35\times 60=21$$となるので、分速$21km$ということになります。

このやり方をマスターすれば、速さの単位変換はばっちりです。
きちんと「時速」、「分速」、「秒速」の意味が分かれば特別なことを覚えなくても単位変換できます。
単位の意味をしっかり掴むことができれば、特別なことを覚えなくても単位を変えることができます。

それでは練習してみましょう。

練習問題

1、秒速$200m$は分速何$km$ですか。

2、時速$45km$は分速何$m$ですか。

3、秒速$15cm$は分速何$m$ですか。

4、分速$30m$は秒速何$cm$ですか。

5、分速$900m$は時速何$km$ですか。

6、秒速$3m$は時速何$km$ですか。

7，時速$72km$は秒速何$m$ですか。

解答と解説

1の解説

秒速から分速に変えるので、$200m$を60倍して、$$200m\times 60=12000m$$となるので、分速$12000m$となります。
あとは$m$を$km$にして、分速$12km$となります。

2の解説

60分間に進む距離$45km$なので、60等分すると分速にする事ができます。$$45\div 60=0.75$$となるので、分速$0.75km$となります。
$km$を$m$にして、分速$750m$となります。

3の解説

秒速を分速になおすので$15cm$を60倍して、$$15cm\times 60=900$$となるので、分速$900cm$となります。
$cm$を$m$になおして、分速$9m$となります。

4の解説

60秒間に$30m$進むので60等分して秒速にします。$$30\div 60=0.5$$となるので秒速$0.5m$となります。
$m$を$cm$になおして、秒速$50cm$ということになります。

5の解説

1分間に$900m$進むので60倍して、$$900m\times 60=540000$$となるので時速$54000m$となります。
$m$を$km$になおして、時速$54km$ということになります。

6の解説

少しややこしい問題を混ぜてみました。
一気に秒速から時速になおしてみましょう。
1時間は$3600秒$なので、秒速$3m$を$3600$倍します。$$3\times 3600=10800$$となるので、時速$10800m$となります。
$m$を$km$になおして、時速$10.8km$ということになります。

秒速から時速にするのが厳しいときは、一旦分速になおしてから、時速にするというのも勿論ＯＫです。
1分は60秒なので、秒速$3m$を$60$倍します。$$3\times 60=180$$となるので、分速$180m$となります。
1時間は60分なので、さらに60倍して、$$180\times 60=10800$$となり、時速$10800m$と分かりました。
あとは$m$を$km$にして、時速$10.8km$となります。
順番にきちんと手順を踏んでやってみると意外とできるモノですよ。