小学校で習う場合の数の3つ目が、繰り返しの場合の数です。
よくコインを投げたときの、表と裏のでる通り数を数える問題が出題されます。
今回の記事では、コイントスを繰り返した時の場合の数を漏れなく数える方法について説明します。
小学生の繰り返しの場合の数の数え方は?コインの表裏は何通り?
それでは例題をもとに数え方を説明します。
場合の数の基礎は数えることです。
今回ももちろん数えます。
樹形図を書いて、数えてみます。
1 回目に出るのは表と裏の2通りです。
下の図のように書き出します。

次に2回目のコインの出方を書いていきます。
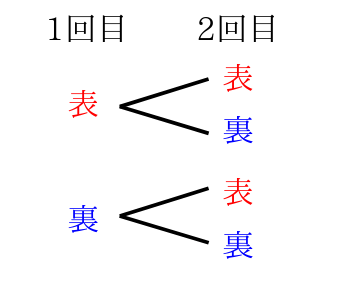
つまり、コインを2回続けて投げたときの、表と裏の出方は、全部で(表,表)、(表,裏)、(裏,表)、(裏,裏)の4通りと言うことになります。
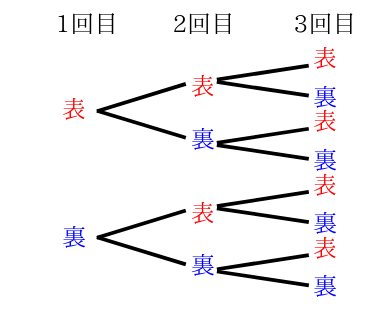
さらに、コインを続けて3回投げたときの、表と裏の出方を数えてみましょう。
先ほどの2回コインを投げたときの図に、さらに3回目の出方を書き加えます。
樹形図が上手く書けないときはどうしたらいいの?
樹形図を使った数え方は、なかなか上手い数え方です。
しかし、お子さんによっては上手く樹形図を使えないということもあると思います。
書き方としては樹形図は便利で分かりやすいのですが、なんだか上手くのみこめないお子さんもいます。
そんな時は下記の記事を参考にしてみてはいかがでしょうか。
・場合の数で習う順列(並べ方)の問題が苦手な小学生への教え方はこちら
まとめ
今回の記事では、繰り返しの場合の数について説明しました。
場合の数の単元は、どうもれなく、ダブりなく数えるのかが大切です。
適当に数えると、漏れが出てしまったり、2回同じものを数えてしまったりしてしまいます。
場合の数の単元では、そういうミスのない数え方をマスターさせることが大切です。
小学校で配布されるドリルや問題集では、そんなに数字が大きくないため、適当に数えても答えがあってしまいます。
この単元ではあくまで過程が大切です。
大事なのは、いかに数え上げるのかということです。
答えがあっても適当に数えていると、どうしてもミスがでます。
さらに先を考えると、中学でもこの考え方を使うので、しっかりマスターしてもらいましょう。
コインの裏表の通り数を計算で求めることもできます。
しかし、小学生に計算で求める方法を教えるのはあまりおすすめではありません。
どんな式を立てればいいのかということにばかり目に行くようになってしまいます。
数え方がきちんとできれるようになれば、全部書くのがだんだん面倒になってきます。
そうなってくると自然と自分で計算で求めるようになる子もでてきます。
うまく樹形図などを使って一部は計算を使って…という感じでできるようになるといいですね。
【関連記事はこちら】
・計算するから難しい!小学生の場合の数は「数え方」が大事!