算数の基礎というと計算というイメージがありますが、場合の数の基本は計算ではありません。
場合の数の基礎は、数えるということ。
そのためにはどんな風にして数えるのかが重要になってきます。
今回の記事では、小学生向けの場合の数、順列(並べ方)について書いてみたいと思います。
場合の数の単元の順列(並べ方)の問題が苦手な小学生への教え方
場合の数における順列(並べ方)というのは、人や物などを並べるということです。
例えば3人の人を並べるようなことをいいます。
それでは、例題と用いて場合の数、順列(並べ方)の数え方をみていきましょう。
3人が1列に並ぶとき、並び方は全部で何通りになりますか。
3人を順番に並べる問題です。
この問題を解くとすると、親御さんの中には\(3!\)や\({}_3 \mathrm{P}_3\)、\(3\times 2\times 1\)という感じで解く方もいらっしゃると思います。
しかし、小学生の段階では、数えるのが基本的です。
学校で習うのも数える形のなので、通り数を数えるやり方がお子さんの混乱を招かずに済みます。
数えるということは、全て書き出してしまうのが基本です。
それでは全て書き出してみましょう。
順列を全て書き出す解き方
1番目を\(A\)さんとします。

次に2番目を\(B\)さん、\(C\)さんとします。
 これで1通り書くことができました。
これで1通り書くことができました。
1番目が\(A\)さんの場合はまだあるので、さらに書き出していきます。

これで\(A\)さんが一番目に来る場合は全て書き出すことが出来ました。
次に\(B\)さんが一番目に来る場合を書き出していきます。

同じように\(C\)さんが1番目に来る場合を書き出していきます。

あとは書き出したものを数えていきます。

これで、\(A\)さん、\(B\)さん、\(C\)さんの3人の並べ方は6通りということが分かりました。
この書き方が一番の基本です。
お子さんが分かりにくいというときはまずはこの書き方で書き出してみましょう。
次に樹形図を使って書き出してみましょう。
樹形図を使って順列を全て書き出すやり方
まずは\(A\)さんが一番目の並び方を樹形図で書きます。
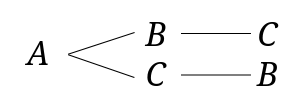
樹形図の一部分を書けたら、お子さんに意味を教えてあげましょう。
全ての並び方を書き出したものと比較しながらお子さんに見せてあげると分かりやすいと思います。

さらに\(B\)さん、\(C\)さんが一番目の並び方を書き加えます。
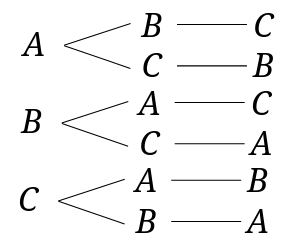
あとは数えて答えを出します。
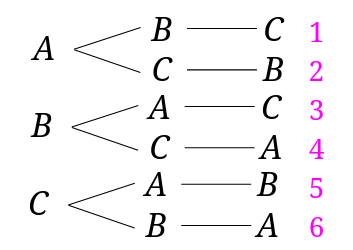
これで6通りということが分かりました。
まとめ
全部を書き出す方法と、樹形図で書く方法を比べてみると少し樹形図の方が楽に見えますね。
この場合はまだ3人しかいないため、どちらで書いてもそんなに手間は変わりません。
書き出すのがお子さんが苦手な場合は、まずは全部書き出すのが良いと思います。
まずは、全ての通り数を書き出せるようになれればOKです。
きちんと全部の通り数を書き出すことができるようになったら、次は、樹形図で全ての通りを書けるようにしましょう。
もちろん全部の通りを書き出すことができれば答えまでは出すことができます。
しかし、人数が増えていくと、全部書き出す方法では、書く量が増えて大変になってしまうので、樹形図の書き方で書くのがおすすめです。
樹形図の意味が分からなくて樹形図を書くことができないということもあるので、書けないときは樹形図の意味を教えてあげるとできるようになることもあります。
どうにもならないときは、全部の順列(並べ方)を書き出せるようになることを目標にするといいですよ。
【関連記事はこちら】
・計算するから難しい!小学生の場合の数は「数え方」が大事!



