順列(並べ方)とはまた違った数え方をしないといけない組み合わせ。
うまく数えるコツをつかめるととても楽に問題を解くことが出来る単元になります。
今回の記事では、組み合わせの数の数え方について書いてみたいと思います。
小学校で習う場合の数の組み合わせの考え方って?
例題を使って、組み合わせの色々な数え方を見ていきましょう。
このうち2枚を選ぶ時の組み合わせは全部で何通りありますか。
組み合わせの数え方①
横に赤、青、黄、黒の文字を書きます。
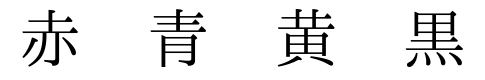
次に左から順番に下の図のように線で結びます。
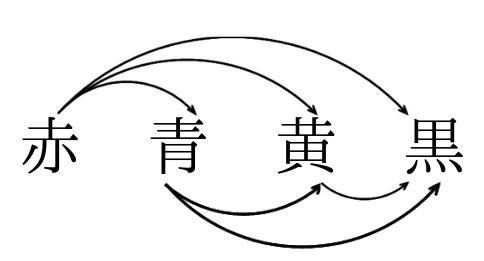
後はその線の数を数えます。
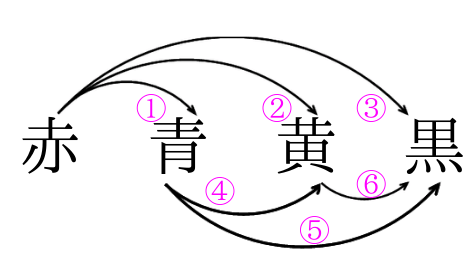
線の数は6本なので、6通りという事が分かります。
コツは番号を振っている順に数えることです。
適当に数えていくと、どこまで数えたのか分からなくなってしまいます。
この数え方は、いくつかのモノから2つの組み合わせを見つけるにはオススメです。
組み合わせの数え方②
図のように赤、青、黄、黒の文字を書きます。
3文字以上が同一直線上にならないように書くのがコツです。

赤、青、黄、黒の全てを線で結びます。
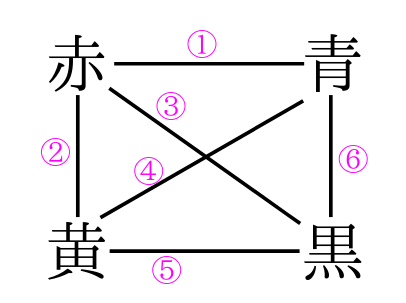
あとは引いた線の数を数えると6本なので、答えは6通りとなります。
組み合わせの数え方③表を使った数え方
表を下のように書きます。
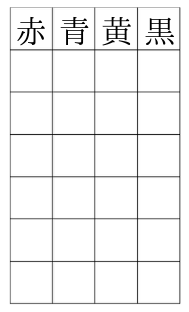
まずは赤を必ず選ぶ場合を考えます。
赤の部分に丸印をいれます。
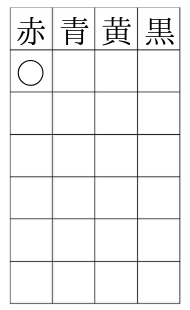
次に右隣の青にも印を入れます。
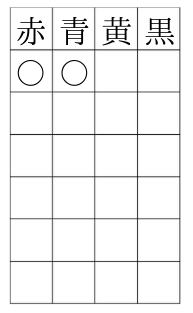
四角で囲んだ部分で1通りとみます。
四角の中は、赤と青を選んで、黄と黒を選ばなかったという意味です。
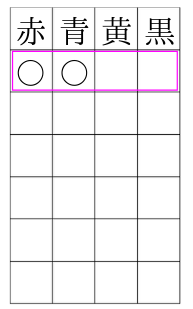
赤を必ず選ぶ通りを全て埋めていきます。
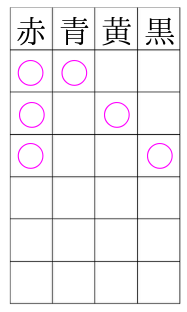
赤を選んだ場合は全部で3通りと分かりました。
次に青を選んだ場合を全て書き出してみます。
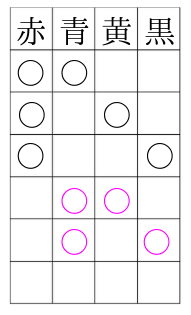
残りの黄と黒の部分に丸を書き入れます。
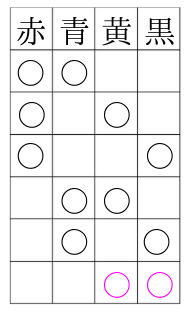
全部書き出したら数を数えます。
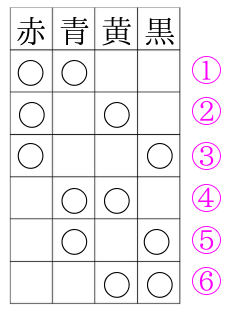
これで6通りが答えという事が分かりました。
組み合わせの数の数え方④表を使った数え方
リーグ戦(総当たり戦)の時に使う下のような表を書きます。
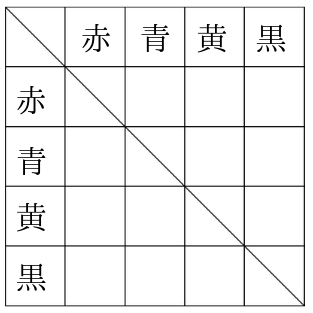
あとは、右上半分を数えて6通りという事が分かります。
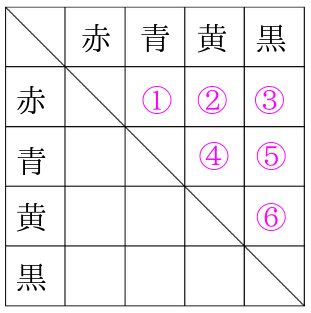
まとめ
今回の記事では、組み合わせの数の数え方について書いてみました。
特に計算がでてくるという訳ではないので、算数の中ではかなり異色な単元ではないでしょうか。
数えればいい、と見ることができると易しく見えますが、そう見えないと難しい単元に見えることがあります。
しばらくして予告なく場合の数の問題を解くときに、計算式が立たずに「うーん…」と悩んでしまうお子さんは一定数います。
算数というと式を立てないといけない、という偏見などがあるとはまりやすくなります。
苦手そうに見えても数えて良いことが分かるだけでスムーズに問題が解けるようになる子もいます。
もし、お子さんが場合の数を苦手としている時には、数えていいということを伝えてあげるだけで解けちゃうこともあります。
まずは解き方(数え方?)を覚えるというよりも、数えてもいいということを認識させることが重要かもしれません。
【関連記事はこちら】
・計算するから難しい!小学生の場合の数は「数え方」が大事!




