電車がトンネルに入り始めてから完全に通過するまでの速さの問題の解き方は？

速さの応用問題でよく出てくる電車の問題。
トンネルをくぐってみたり、鉄橋を渡ってみたりすれ違ってみたり…
色々なパターンがありますが、1つずつ覚えて解くのは本当に大変です。
できれば普通に考えたら解ける！と言いたいところですが、文章題の内容の整理が上手くいかず解けないという子もいます。
そもそも、全く分からないという子も結構いますが…

この記事では、電車がトンネルを通る問題を扱っていきます。

電車がトンネルに入り始めてから完全に通り抜けるまでの通過算の問題を解説

電車がトンネルを通る問題って難しいと感じるお子さんが多いです。
その1番の原因は電車の長さ。
人やバスが問題の題材だったときは、それらを1つの点として考えることができます。
例えばある地点にバスが到着した時を考えるとバスの前の部分が目的地に到着したのか、それともバスの車体が全部到着したのかを考える問題はまず出ません。
しかし、電車の問題の時は、電車の長さまで考えないといけなくなるため、人やバスなどが問題に出る問題と比べると情報が1つ増えてしまいます。
この1つ増えた電車の長さという情報のせいで、お子さんが問題を解いているうちに大混乱…という事態になってしまいます。
そんなことにならないように、うまく図を使って解いていきたいと思います。

それでは例題を見ていきましょう。

電車がトンネルを通る問題の難しいところは電車に長さがあることです。
この長さをどう考えたらいいのかが、電車がトンネルを通る問題のコツでもあります。
この手の問題は、一言で言えば絵図を書くと結構簡単に解けてしまいます。

早速、絵図を書いて解いてみましょう。
絵図というのは、そのまま問題文を絵にするということです。
もちろん、簡単な絵でOKです。
芸術的に描く必要はありませんよ。
こんな感じでOKです。
ほんとに簡単ですよね。
こんなのでも描けないという場合は単純に長方形ををかいてこれが電車…みたいな感じでOKです。
この問題では電車がトンネルに入り始めてから完全にトンネルから出るまでということなのでまずはその状況を理解しないと解けません。
それぞれの場合を絵図で示してみますね。

トンネルに入り始めたとき
トンネルから完全にでたとき
この2つの絵図を比較してみると電車が動いた距離がどれだけなのかをイメージしやすくなります。
電車の先頭を基準に考えますよ。
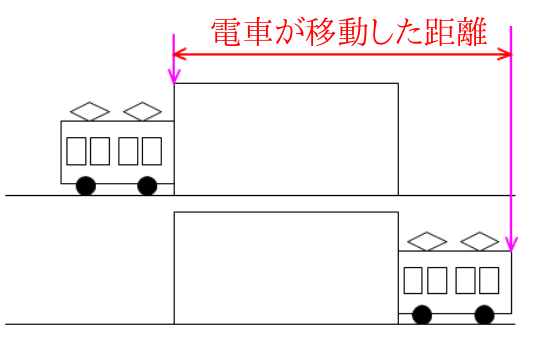図から電車が移動した距離がトンネルの長さと電車の長さの合計になるということが分かりました。
それでは計算していきましょう。

移動した距離がトンネルの長さ＋電車の長さなので、$$100+1700=1800$$電車の速さは秒速\(30m\)なので、$$1800\div 30=60$$電車がトンネルに入り始めてから完全にでるまでに60秒かかったことが分かります。
速さの単元では応用問題に分類されると思うのですが、絵図がきちんと書けると情報の整理もきちんとできるので解きやすくなりますよ。

それでは、もう1題例題を解きますね。

今度は単位がごちゃごちゃしているのでまずは単位を揃えましょう。
分速\(1.8km\)を秒速○\(m\)の形にします。
\(km\)を\(m\)に変えて、分速\(1800m\)。
さらにこれを60で割って、秒速にします。$$1800\div 60=30$$
この速さで電車は9秒進んだので、電車が移動した距離は、$$30\times 9=270$$
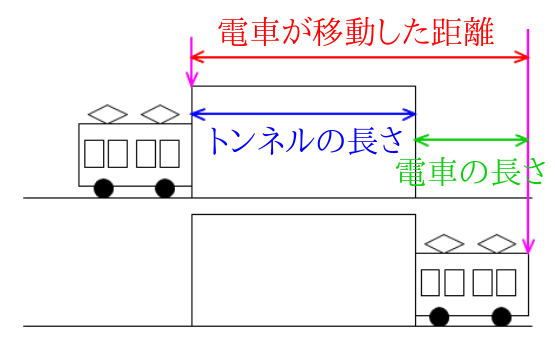電車が移動した距離は先ほどの例題と同じで、トンネルの長さと電車の長さの合計です。
電車の長さは\(80m\)、移動した距離は\(270m\)なので、トンネルの長さは、$$270-80=190$$トンネルの長さは\(190m\)ということが分かりました。

先ほどの例題よりもやりにくい感じでしたね。
分からない時ほど絵図が役に立ちます。

お子さんが全くわからない！とい言っているような状況であれば絵図を描かせるのはいい手だと思います。
絵図の基本は問題文にある物をそのまま描くということです。
電車が出てくれば電車を描くし、いちごがでてくればいちごを描くという感じです。
こうすることで全く何もしない、手を出さないという状態ではなくなるのでおすすめですよ。

練習問題

1、長さ\(3.4km\)のトンネルがあります。
全長\(200m\)の電車が時速\(108km\)でそのトンネルを通るとき、電車がトンネルに入り始めてから完全に出るまで何秒かかりますか。

2、\(720m\)のトンネルを5両編成の電車が秒速30mの速さで通りました。
電車がトンネルに入り始めてから完全に通り抜けるまで27秒かかります。
電車は1両何\(m\)ですか。

3、長さ\(90m\)の電車が\(1800m\)のトンネルを通りました。
このとき、電車がトンネルに入り始めてから完全に通り終わるまで54秒かかりました。
電車は時速何\(km\)でトンネルを通りましたか。

解答と解説

1の解説

単位がバラバラなので、まずは単位を揃えましょう。
トンネルの長さを\(3.4km\)から\(3400m\)に、電車の速さを\時速(108km\)から秒速\(30m\)にします。
電車がトンネルに入ってから完全に出るまでなので、移動した距離は電車の長さ＋トンネルの長さになります。
トンネルの長さと電車の長さの和を秒速\(30m\)でどれだけかかるのかを求めればいいので、$$(3400+200)\div 30=120$$求める答えは120秒ということになります。

2の解説

少しだけ手間が増える問題ですね。
まずは電車の長さを今まで通り求めていきましょう。
電車が移動した距離を求めます。
秒速\(30m\)で27秒移動したので、$$30\times 27=810$$
この電車が移動した距離は、トンネルの長さ＋電車の長さなので、移動した距離とトンネルの長さの差が電車の長さになるので、$$810-720=90$$電車は5両編成なので、これを5で割って、$$90\div 5=18$$電車1両の長さは\(18m\)となります。

3の解説

電車が移動した距離がいくらかをまずは考えます。
この時の電車が移動した距離は、トンネルの長さ＋電車の長さになるので、$$90+1800=1890$$\(1890m\)を進むのに54秒かかったので、$$1890\div 54=35$$この電車の速さが分速\(35m\)ということが分かりました。
問題で聞かれているのが時速○\(km\)という形なので、単位を合わせます。
まずは時速にすると、$$35\times 3600=126000$$あとは単位を\(km\)に合わせて、答えは時速\(126km\)となります。

ここの問題のポイントは電車が移動した距離が何に当たるかということです。
問題を読んだだけで判断できるお子さんはかなり少ないと思います。
大人でも難しいのではないでしょうか。

絵図をうまく使うといいですよ。

まとめ

今回の記事ではトンネルを通る電車の速さの文章問題を扱いました。
問題を解く以上に問題文が何を言っているのかを把握することが難しい問題です。
読んでわからないときは図を描くということを徹底できるとうまく解けるようになりやすいと思います。
少し違った電車とトンネルの問題はこちらの記事を見てみてください。

分からないときは図。
全く分からないというときこそ絵図がおススメですよ。

【関連記事はこちら】
・電車がトンネルの中に完全に入ってから出始める時の通過算の問題の解き方とは？

・電車が鉄橋を渡り始めてから完全に渡り終わる通過算の解き方は？