電車がトンネルの中に完全に入ってから出始める通過算の問題の解き方とは？

小学生の速さの単元で登場する電車とトンネルの問題は難しく感じるお子さんが多いと思います。
まず1番にすべきは、どこからどこに電車が移動するのかを把握することです。
きちんと問題の意味の把握ができれば問題のレベルをグッと落とすことができます。
まずは問題の意味、題意をしっかりつかめるようにするといいですね。

今回は電車がトンネルの中に完全に入ってから出始める時の速さの問題について扱っていきます。

電車がトンネルの中に完全に入ってから出始める時の速さの問題が解けるようになろう

それでは早速例題を用いてみていきましょう。

電車とトンネルの出てくる問題では、まずは問題文の理解が最も大切です。
ここをクリアしないことには、算数の問題として解くところまで行きつくことができません。
まずはゆっくり、正確に問題文を読んでもらいましょう。

この問題のポイントは何といっても、問題文の「この電車がトンネルに入り終わってから出始めるまで」の解釈ができるかというところにあります。
ここが読み取れるかというのがポイントで、問題を解けるか解けないかが大きく決まります。
(読み取れなければどうしようもなくなってしまいますが…)
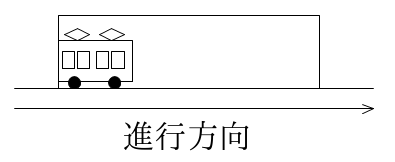
スタート地点は、「電車がトンネルに入り終わってから」ですね。
電車がトンネルに入り終わってからというのは、電車がトンネル内にきれいに入ったところがスタートという意味です。
電車がトンネルにきれいに入った状況を絵にするとこんな感じになります。
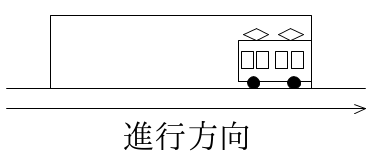
次にこの電車がどこまで行ったときがゴールなのかというと「出始めるまで」となっています。
この電車がトンネルを出始めるまでを図にすると、こんな感じになります。
スタート地点とゴール地点が分かったので、次にこの電車が移動した距離を考えましょう。
スタート時の図とゴール時の図を縦に並べると分かりやすくなります。
電車の移動した距離は電車の先頭の部分が移動した距離で考えるといいと思います。^[1] … Continue reading

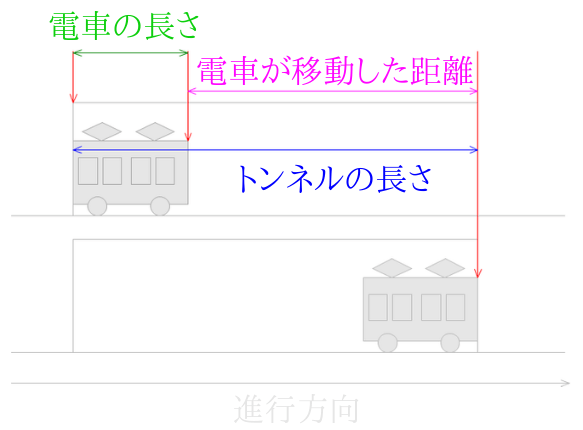きちんと図が描けると理解しやすいですね。
図から、電車の移動した距離は、トンネルの長さから電車の長さを引けば出せることが分かりました。
さらにこの図に数字を書き込んであげると分かりやすくなります。
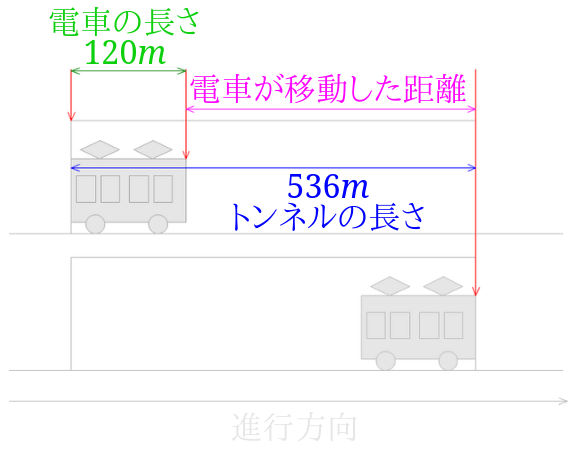電車の長さ( \(120m\) )とトンネルの長さ( \(536m\) )に数字を入れてみました。
電車が移動した距離は、トンネルの長さから電車の長さを引けばいいので、$$536-120=416$$秒速\(32m\)となります。
例題では電車がトンネルに入り終わってから出始めるまでにかかった時間が聞かれているので、$$416\div 32=13$$答えは13秒ということになります。

問題文を読んだだけでは、考えにくかった問題が、図を描くことで随分易しくなりました。
図を描いたりすることで問題のレベルを下げることができます。
うまく問題文を図にできると解きやすくなりますね。

それではもう1題例題を解いてみましょう。

求める単位が\(m\)なので、トンネルの長さの単位を\(m\)に、速さの単位は時速〇\(km\)から秒速△\(m\)に、時間の単位は秒から分に単位変換します
つまり、トンネルの長さ\(3.08km\)は\(3080m\)に、時速\(90km\)は分速\(1500m\)に、120秒は2分にします。
この電車は分速\(1500m\)で120秒移動ました。
この電車が移動した距離を求めると、$$1500\times 2=3000$$と、なります。
今回の例題も前の例題と同じように問題を図にします。
「完全にトンネルに入ってからトンネルを出始めるまで」が電車の移動距離なので、前の例題で最後に書いた図にこの例題の長さを書き込んでみます。
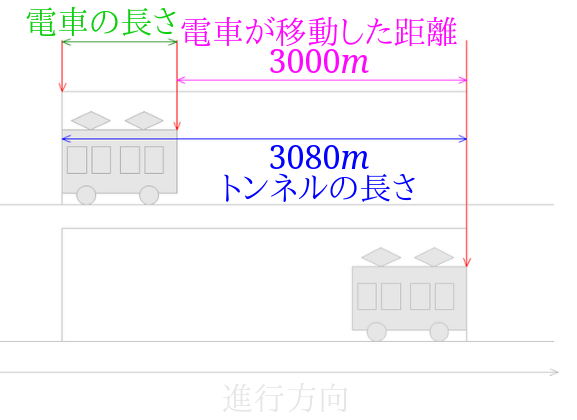電車の長さは、トンネルの長さと電車が移動した距離の差なので、$$3080-3000=80$$電車の長さは\(80m\)ということになります。

練習問題

1、長さ\(180m\)、分速\(1.8km\)の電車があるトンネルに入りきってから出始めるまでに150秒かかりました。
このトンネルの長さは何\(m\)ですか。

2、長さ\(3500m\)のトンネルを長さ\(0.2km\)の電車が通り抜けました。
この電車がトンネルに完全に入ってからどんネルを出始めるまでにかかった時間は165秒です。
電車は分速何\(m\)でトンネルを抜けましたか。

3、8両編成の電車が長さ\(1.052km\)のトンネルに入り終わってから出始めるまで30秒かかりました。
このとき、電車は時速\(108km\)で走っていました。
この電車1両は何\(m\)ですか。

解答と解説

1の解説

まずは電車の移動距離を求めましょう。
単位が\(m\)なので、分速\(1.8km\)の単位を\(m\)に単位変換すると分速\(1800m\)となります。
また150秒は\(\frac{150}{60}\)分なので電車の移動距離は、$$1800\times \frac{150}{60}=4500$$
図で今までに出てきた長さの関係を確認してみます。
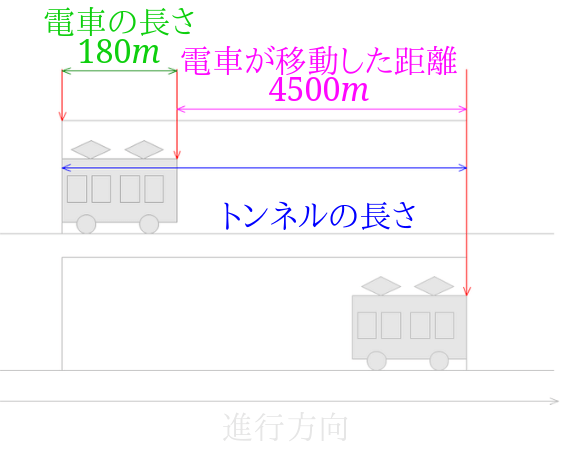トンネルの長さは、電車の長さと電車が移動した距離の和なので、$$180+4500=4680$$トンネルの長さは\(4680m\)と分かりました。

2の解説

まずは図で長さを確認してみましょう。

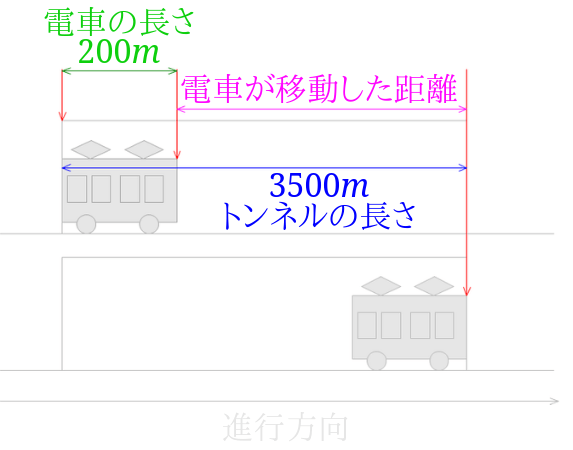
電車が移動した距離は、トンネルの長さと電車の長さの差なので、$$3500-200=3300$$電車が移動した距離は\(3300m\)と分かりました。
\(3300m\)進むのに165秒かかったので、$$3300\div 165=20$$秒速\(20m\)となります。
答えは分速○\(m\)の形で答えないといけないので、分速に単位変換をして、$$20\times 60=1200$$答えは分速\(1200m\)となります。

3の解説

まずはこの電車の移動した距離を求めます。
時速\(108km\)を秒速○\(m\)に単位変換すると秒速\(30m\)となります。
電車が移動した距離は、秒速\(30m\)で30秒すすんだ距離なので、$$30\times 30=900$$ここで図を描いて数字を整理しましょう。
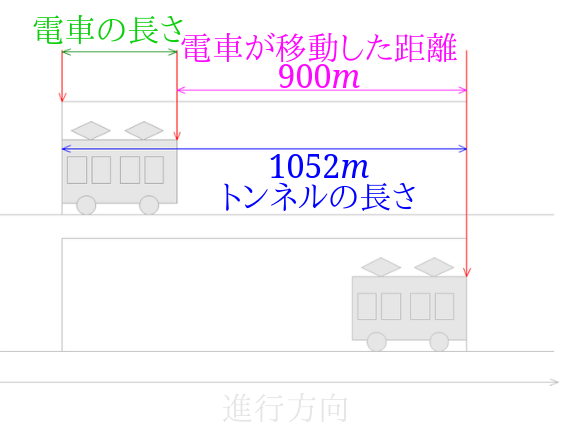電車の長さは、トンネルの長さと電車が移動した距離の差なので、$$1052-900=152$$またこの電車は8両編成なので、$$152\div 8=19$$この電車1両の長さは\(19m\)となります。

1つ1つの式に応用的な要素はありません。
難しいのは問題の解釈です。
ややこしい問題ほどきちんと図を書くことで楽に解けることになります。
「わからない！」とお子さんの手が止まるようであれば、一緒に電車の絵などを描きながら楽しく教えてあげるといいですね。

まとめ

今回の記事では電車がトンネルの中にきれいに入ってしまってから出始めるまでの速さの問題についてでした。
速さの問題の中ではかなり難しい部類の問題になると思います。
ただ1つ1つきちんとしていけば基礎的な知識と図を書くことで上手くいきます。
この解き方を教えるときの1つの難関が図が書けるかということです。
もう分からないと思い込んでいる子は、描いたところで無駄と思っていることも多く図を描かせるのにも一苦労ということがあります。
気長にゆっくり絵を描きながら解けるようになればいいのではないでしょうか。
1日でマスターしようと思っても難しいので少しずつ理解して解けるようになるといいですね。

【関連記事はこちら】
・電車がトンネルに入り始めてから完全に通過するまでの速さの問題の解き方は？