電車が鉄橋を渡り始めてから完全に渡り終わる通過算の解き方は？

速さの問題でよく見かける鉄橋の文章問題。
トンネルの問題と大差はありませんが、そのちょっとした違いはお子さんからすると全く違うモノに見えてしまいます。
教える側からすれば「同じ解き方で解けるのに、なぜ解けないの？」という疑問がわくこともあるかもしれませんね。
しかし、子どもたちにとって、ちょっと題材が変わるというのは大きなポイント。
全く違う問題に見えることもあります。
トンネルと言えばイメージがしやすく、大体誰しもが似たようなものを思い浮かべると思います。
だけど、これが鉄橋となるとどうでしょう。
鉄橋の形などが色々重い浮かぶ方もいれば、橋は思い浮かぶけど鉄橋かな？ちがうのかな？なんて方もいらっしゃるかもしれませんね。
絵を描こうと思っても鉄橋は難しいなぁと私も思います。
子どもたちが解きにくいのはやはりイメージがわきにくいからという理由であることが多いです。

しっかりイメージしながら解いていけるようになれるといいですね。

電車が鉄橋を渡り始めてから完全に渡り終わる通過算の問題を解こう！

今回の記事では鉄橋を渡る電車を題材にした通過算の文章問題を扱います。
算数の速さの単元でよく出てくる鉄橋問題。
しっかり絵を描きながら解くのがポイントです。

それでは早速例題からみていきましょう。

例題

長さ$60m$の電車が長さ$420m$の鉄橋を渡ります。
電車が秒速$30m$で走っていたとき、電車が鉄橋を渡り始めてから渡り終わるまでにかかる時間は何秒ですか。

まずは鉄橋と電車の絵を描いてみましょう。
下手くそですがそれなりに描けました。
もちろんもっとリアリティのある鉄橋や電車を描いてもOKです。
お子さんが電車が好きだったりすると電車の絵に気合いが入ってしまうかもしれませんね。

まずは電車のスタート地点を確認しましょう。
「鉄橋を渡り始める」時がスタートです。
図に描いてみましょう。
こんな感じですね。
渡り始めるときなので、電車の頭が鉄橋にかかったときですね。
これでスタートが分かりました。
次にゴールを確認しましょう。
「渡り終わる」時がゴールです。
また図に描いてみましょう。
こんな感じですね。
「渡り終える」時がゴールなので、電車のおしりが橋を渡り終えたときになります。
この2つの図を使って電車の移動距離と電車の長さと鉄橋の長さの関係を図で描いてみましょう。
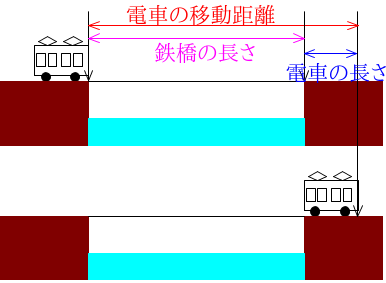こんな感じですね。
それではこの図をもとに例題を解きますね。
電車の長さ$60m$と鉄橋の長さ$420m$を書き込んでみます。

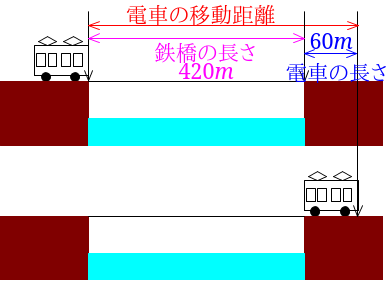
図から電車の移動距離が分かります。
電車の移動距離は、電車の長さと鉄橋の長さの和なので、$$60+420=480$$この電車の速さは秒速$30m$なので、この電車が鉄橋を渡り始めて渡り終わるまでにかかった時間は、$$480\div 30=16$$答えは16秒となります。

きちんと図を描くと随分楽になりますね。
格好いい図を書く必要はないので、しっかり電車を描けばOKです。
お子さんが絵を描くのが好きな場合は楽しみながらできればいいですね。

それでは次の例題を解いてみましょう。

例題

電車が鉄橋を渡り始めてから渡り終わるまでに8秒かかりました。
電車の長さは$90m$です。
この電車が時速$126km$で進んでいたとき、鉄橋の長さは何$m$になりますか。

まずは電車が進んだ距離を出してみましょう。
時速$126km$を秒速○$m$に単位変換すると、秒速$35m$となります。
電車は秒速$35m$で8秒進んだので、$$35\times 8=280$$図に描いてみましょう。
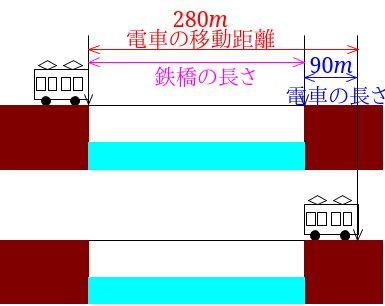鉄橋の長さは、電車が移動した距離と電車の長さの差なので、$$280-90=190$$鉄橋の長さは$190m$となります。

図を描くと思っているほど難しくないのではないでしょうか。
大人でも何も描かずに解くのは難しいですからね。
簡単にでも図を描くことがおススメですよ。

練習問題

1、長さ$120m$の電車が鉄橋を渡り始めてから渡りきるまでに18秒かかりました。
鉄橋の長さが$492m$のとき、電車は分速何$m$で鉄橋を渡ったことになりますか。

2、6両編成の電車が長さ$872m$の鉄橋を渡ります。
この電車が時速$111.6km$の速さで鉄橋を渡り始めてから渡り終わるまでにかかった時間は32秒でした。
電車1両の長さは何$m$ですか。

3、1両$18m$の4両編成の電車が時速$100.8km$で走っています。
この電車がある鉄橋を渡り始めてから渡り終えるまでの時間は28秒でした。
鉄橋の長さは何$m$ですか。

解答と解説

1の解説

まずは図に描いて数字の整理から始めましょう。
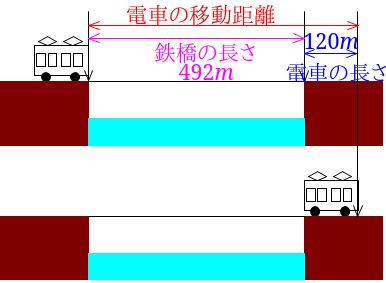図から、電車の移動距離を求めましょう。
電車の移動距離は、電車の長さと鉄橋の長さの和なので、$$120+492=612$$この電車が鉄橋を渡り始めてから渡り終るまでに18秒かかったので、$$612\div 18=34$$秒速$34m$と分かったので、これを分速にして、答えは分速$2040m$となります。

2の解説

まずはこの電車が移動した距離を求めましょう。
時速$111.6km$を秒速○$m$に単位変換すると、秒速$31m$となります。
この電車は秒速$31m$で32秒移動したので、移動した距離は、$$31\times 32=992$$図に描いて整理しましょう。
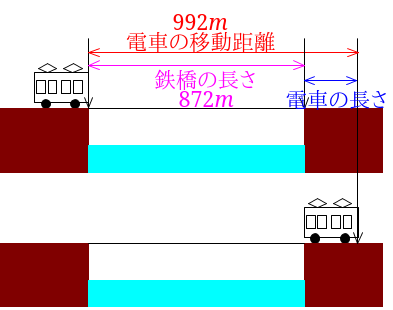電車の長さは、電車の移動距離と鉄橋の長さの差なので、$$992-872=120$$電車は6両編成なので、$$120\div 6=20$$電車1両の長さは$20m$となります。

3の解説

まずはこの電車の移動距離を求めます。
時速$100.8km$を秒速○$m$の形に単位変換すると、秒速$28m$となります。
この電車が、秒速$28m$で28秒移動するので、$$28\times 28=784$$電車の長さは、1両$18m$の4両編成の電車なので、$$18\times 4=72$$数字を図で整理してみます。
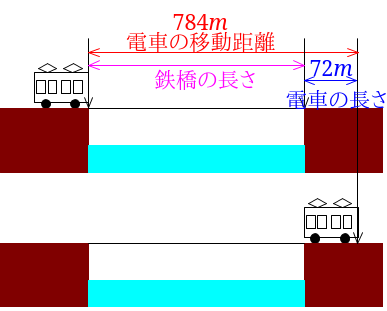図を見ると鉄橋の長さは、電車の移動距離と電車の長さの差なので、$$784-72=712$$鉄橋の長さは$712m$となります。