掛け算九九は覚える事ができたでしょうか。
苦戦するお子さんは結構苦戦します。
シュッとできなくても、時間を掛けてできるようになれば大丈夫だと思います。
焦らず日々コツコツすることが大切ですよ。
掛け算九九が言えるようになったら、次は文章問題です。
きちんとなぜ掛け算を使うのかを意識しながら解けるようになると良いと思いますよ。
今回の記事では小学2年生の掛け算の文章問題を扱ってみたいと思います。
かけ算の文章問題で式が立てられないときはどうやって解く?
それでは早速例題をしてみましょう。
絵図を用いて解いてみましょう。
3人、人がいるので、人を書いてみましょう。
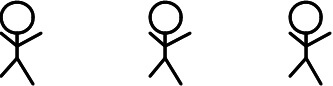
1人に4個ずつあめ玉を配るので、4つずつあめ玉を書いていきます。
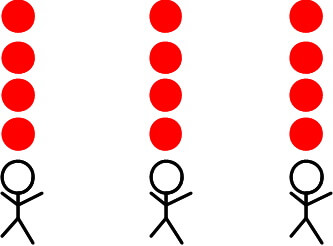
あめ玉が、いくつあるか分かればいいので、答えは12個となります。
ここまできちんと絵図を描くことができれば、あめ玉の個数を数えれば答えが出せますね。
一応、式を書くことを考えてみると、4個のあめ玉のかたまりが3つあるので、$$4\times 3=12$$となり、答えは12個ということになります。
もう1題例題を見てみましょう。
ちょっとひねりがきいた問題です。
5人に2つずつ配ろうとしたんですね。
すると、1つみかんが、足りません。
まずは、5人に2つずつみかんを配れたとして絵図を描いてみましょう。

実際には、みかんを5人に2つずつ配ると、1つ足りませんでした。
絵図から、みかんを1つ消してしまいましょう。

はじめにあったみかんの個数は、9個となります。
式を用いて解くいてみます。
まずは5人に2つずつみかんを配ることができたときのみかんの数を求めましょう。$$2\times 5=10$$5人に2つずつみかんを配ると1つ足りなかったので、ここからみかんを1つ引きます。$$10-1=9$$よって、みかんの個数は9個となりました。
分からない時は絵図が基本です。
また、掛け算がすらすらできないときは、ゆっくりでいいので慣れていけるといいと思います。
練習問題
1、リボンがあります。
このリボンを\(8cm\)ずつ切って、4本作ると、\(2cm\)あまりました。
①\(8cm\)のリボンを4本作るには、リボンは何\(cm\)必要ですか。
②はじめにあったリボンは何\(cm\)ですか。
2、1たば5まい入りの色紙を3たばずつ、2人にくばりました。
色紙は全部で何まいありましたか。
3、花子さんはシールを12まい持っています。
花子さんのお姉さんは花子さんの3倍のシールを持っています。
花子さんのお姉さんはシールを何まい持っていますか。
解答と解説
1の解説
①からみていきましょう。
\(8cm\)のリボンを4本作ることを絵図にしてみましょう。

\(8cm\)が4本あるので、$$8\times 4=32$$\(8cm\)のリボンを4本作るには\(32cm\)必要なことが分かりました。[1]\(8+8+8+8=32\)でもOKですよ。足し算で全部してしまった場合は掛け算でもできるよーって教えてあげるといいですよ。
・掛け算と足し算は同じように見えて違いがあるの?なぜどっちか使い分けるの?
②をみていきましょう。
\(8cm\)のリボンを4本作ると、\(2cm\)あまります。
絵図にすると、

\(32+2=34\)となり、はじめにあったリボンの長さは\(34cm\)ということになります。
2の解説
そのまま絵図を描いてみます。
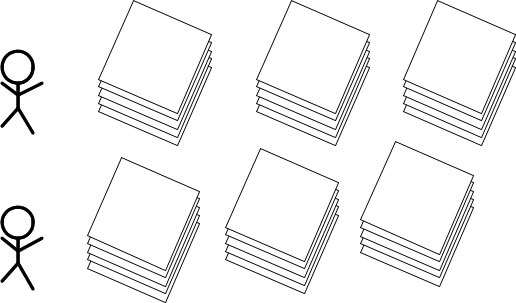
1人が5枚が1束になった色紙を3束ずつ貰ったので、1人がもらう色紙の枚数は、$$5\times3=15$$2人いるので、$$15\times 2=30$$となり、色紙は全部で30枚となります。
この解き方は、1人が貰う枚数を出して、それをもらった人が2人いたと見たのでこんな感じになりました。
ちょっと見方を変えると、5枚の色紙の束が6つあると見ることもできます。
この時の式は、$$5\times 6=30$$となります。
どちらの解き方でもOKですよ。
3の解説
花子さんが12枚シールを持っているということなので、そのまま絵図にしてしまいます。

花子さんのお姉さんは、花子さんの3倍のシールを持っています。
これを絵図にしてみましょう。
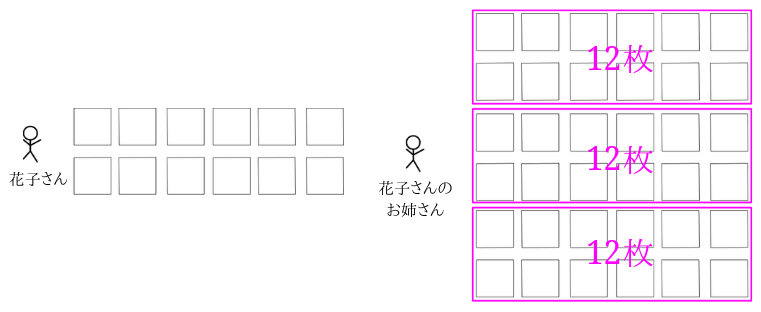
花子さんのお姉さんの持っているシールの枚数は12枚のかたまりが3つあるので、$$12\times 3=36$$花子さんのお姉さんの持っているシールの枚数は36枚ということになります。
まとめ
今回の記事では、小学2年生の掛け算の文章問題を扱いました。
なかなかうまく式が立たないときはまずは絵図を描くのがおすすめですよ。
きちんと問題の意味が分からないと立式なんてしている場合ではなくなってしまいます。
まずは問題文の理解を優先し、式はあまり間がなくても大丈夫です。
しっかり問題文の意味が理解できたあとに、立式をするとOKですよ。
References
| ↑1 | \(8+8+8+8=32\)でもOKですよ。足し算で全部してしまった場合は掛け算でもできるよーって教えてあげるといいですよ。 |
|---|





> 3×4=12 と式を立てると減点されることもあるかもしれません
という点について質問です。
https://twitter.com/golgo_sardine/status/911991833453932544
私の持っている本で、このようになっているのですが、本当にそのような決まりがあるのでしょうか?
ゴルゴ・サーディーンさん、コメントありがとうございます。^^
この掛け算の順番は悩ましいところではありますね。
一応掛け算の意味が、「1つ分の数」\(\times\)「いくつ分」と習っているので、そこを元に考えると順番に意味があることになります。
本来はそんなに神経質にならなくてもいいところだと思うのですが、現実的に小学校のテストで減点されることがあります。
そのため、
> 3×4=12 と式を立てると減点されることもあるかもしれません
と記述しています。
ゴルゴ・サーディーンさんのリンク先の本の記述の部分(赤線が引いてある部分ですよね?)に関しては2つの側面があると思います。
2つというのは、掛け算の意味という側面と長方形の面積の公式という側面です。
\(30\times 2=60\)というのは、\(長方形の面積=たて\times よこ\)から考えての立式だと思います。
しかし、「1つ分の数」\(\times\)「いくつ分」という掛け算の意味からははずれてしまいますね。
無理矢理どちらも満たそうと思えば、面積図を90°回転させるとつじつまは合わせられそうです。
分かりにくくなってしまいますが・・・
掛け算の順番に意味を持たせることそのものは、場合によっては悪くはない気がします。
掛け算の意味を理解させたい時には、掛け算の順番に意味を持たせるのもいいと思います。
しかし、テストで減点された後のその後の先生方の指導の様子を子供たちから聞くと、ただ点数の獲得をするために順番が必要となってしまっているように見えます。
子供たちのその後の学力を伸ばすためということを主眼に置いて考えての行動なのか、それとも単に順番通りに書かないといけないという認識からかで、随分と意味が違ってしまうと思います。
個人的にはどちらでもいいと思うので、一応学校では大人の事情で減点されることがあるから・・・みたいな感じで説明しています。
なぜ減点するのか分かるようにしてという感じです。
レスありがとうございます。
私は、貴サイトで言っておられる
「今まで通り教えてテストではどちらでもいいとしてしまう、という方法では
『テストではどちらで書いてもいいのに授業中だけ順番を考える必要があると
いうことを子どもたちが納得してくれるかが懸念』」
https://sansuwakaru.com/275.html
…という考え方に疑問を覚えます。
私が示しました鶴亀算のほか、学校では日常的に、2年生に叩き込んだ事に反する
事が行われています。
2年生時点でのルールでは
「10分間の2倍を求めよ、というときは 10×2」
「10分間の3倍を求めよ、というときは 10×3」
となる筈ですが、多くの学校で「家庭での学習時間は 学年×10分」と言われています。
http://4sho.wako-city.ed.jp/modules/hp_jmenu/attachfile/file574d1c7d81d2d.pdf
http://www.sakaide.ed.jp/tobu/tebiki.html
http://www.curricen2.hokkaido-c.ed.jp/dokyoi/siryo/meyasu_01P.pdf
http://www.city.sakura.lg.jp/cmsfiles/contents/0000002/2353/kateigakusyuu-ura.pdf
http://www.ome-tky.ed.jp/gakko/gakuryoku/documents/h26gakuryokuchousahoukoku7.pdf
どうせ日常の中で、掛算の順序を守らない見本を見せられてしまうのですから、
授業の中で「どっちでも良い」と明言していただきたいものだと、順序強制に反対する者としては、考えます。
ゴルゴ・サーディーンさん、コメントありがとうございます。
ゴルゴ・サーディーンさんのおっしゃっている「2年生に叩き込んだ事に反する事」ですが、こういった点に関しては、先生個人の教え方が反映される部分であって、統制された教え方ではなかったように思います。
また文部科学省でもこのことを強制しているわけではなかったと記憶しています。
リンク先の、学年\(\times 10\)分という記述のあるプリント類を作った先生は、掛け算の順番を重視した先生なのでしょうか。
ゴルゴ・サーディーンさんのリンク先の鶴亀算の説明は、「掛け算の決まり(1つ分の数\(\times\)いくつ分)」という概念ではなく、小学4年生で習う「\(長方形の面積=たて\times よこ\)」の考え方を使っているのだと思われます。
どちらも学校で習う「計算の決まり」に基づいているので、学校で習う事に反しているとは言いがたいため、一方のみが正解だと決めることは難しいのではないでしょうか。
「授業の中でどちらでも良いことを明言する」ということについて、指摘いただいた章では「もし、学校が掛け算の順番なんか気にしなくてもいいという指導方針になった時に、算数を教える先生はどのような授業をすることになるのか」という事について触れています。
あくまでも。「先生の授業の仕方」について考えたことを書いています。
もし、「授業では順番をきちんと考えるように教えるけれど、テストの採点に関してはそこを見ない」とするとき、子供たちにそれについてハッキリと言及するかは先生次第になるのではないかと思います。
おそらく、そうなった場合、混乱を避けるためにも、授業中やテスト前、テストを返すとき等に明言することがほとんどだと考えています。
掛け算の掛ける順番は、どちらでもいいというのは、ごもっともだと思います。
私もどちらでもいいと思っています。
ただ、掛け算の順番を意識させるのは、初めのうちは多少仕方のない側面もあるのではないでしょうか。
初学者である小学2年生の子供たちにいきなり交換法則を教えるのも大変です。
最近では幼稚園の段階で掛け算九九が出来る子も増えています。
掛け算九九が出来る子供たちは最初から交換法則などの話があっても問題無いかもしれませんが、初めて掛け算を習う子供たちにとってはどうなんでしょうか。
掛け算の順序を考慮せず、どちらの意味も持つということになれば、1つの式に対して、常に2つの理屈が伴うようになります。
例えば\(1\times2\)を教える時も、「1が2つ」という意味と、「2が1つ」という意味を教えるのでしょうか。
ちょっと難しい気がします。
多くの学校での問題に関しては、直接学校に行かれた方がいいのではないでしょうか。
またもうひとつ、「学力のために効果がある」という話も疑問です。
多くの子が「単位の換算」を苦手にしている、と聞いています。
「1.5g を mg に換算する」というとき、
1.5×1000 と
1000×1.5 のどちらにするか、がはっきり決まっていないのですから、子ども達が
苦手になってしまうのは当然だ、と私などは思ってしまいます。
これなどはまさに「どっちでも良い」とすべき問題のように思います。
参考:
http://happylilac.net/keisan-tanni6nen.html
ゴルゴ・サーディーンさん、コメントありがとうございます^^
多くの子どもたちが単位換算を苦手としているという点について、私が見てきた単位換算が苦手な子たちというのは、掛け算の決まり(「1つ分の数」\(\times\)「いくつ分」)に数字を当てはめることができずに混乱して「苦手」となっているというより、単位の構造や意味がよく分かっていないという場合が多いです。
私は今まで見たことがないのですが、一般的にそんなに掛け算の順番で混乱しているお子さんの数は多いのでしょうか?
そもそも、掛け算の決まり(?)に当てはめて、考えようとしているお子さんに会ったことがありません。
掛け算の順番は「どっちでもい良い」とすべきとのことですが、掛け算の導入段階から掛ける順番はどちらでも良いとした方が子どもたちの成績が良かったのでしょうか。
そうであれば、そのことを元に掛け算の順序に意味を持たせることに意味がないことを小学校や文科省などと話された方が建設的だと思いますよ。
レスありがとうございます。
>リンク先の、学年×10分という記述のあるプリント類を作った先生は、
>掛け算の順番を重視した先生なのでしょうか。
これはモットモな指摘です。
では、「掛け算の順番は片方だけが正しい」という指導をすべての小学校でやっている訳ではない、としますと、
一部の学校で「掛け算の順番を守らないと、それは掛け算が判ってないと見なしますよ」
という指導は、子ども達に嘘(余所の学校ではそうでないのだから、嘘です)を叩き込んでいるわけですから、保護者としては困った事です。
(「掛け算の順番を守らないと、判ってないと見なす」という方針は、
ベネッセの漫画に示されています。
https://togetter.com/li/723999)
ゴルゴ・サーディーンさん、コメントありがとうございます^^
「みなす」と、いう言葉が曲者でしょうね。
みなすと言うことは、そもそもそうとは限らないという意味を内包します。
つまり、そのような表現になるということは、掛け算の順番から子供たちの理解をはかるということそのものが、役割を果たすとは言えないということです。
便宜的にそう判断しますよ、ということであり、特に理解している、理解していないということとは関係性が必ずしもあるということではないと思われます。
この判断の仕方に意味があるのかと言えば、疑問符が付くものだと思います。
保護者様という言うことはお子さんが掛け算の順序を重視する先生に指導されているのでしょうか。
もしそうであれば、直接先生に尋ねてみてもいいと思いますよ。
ゴルゴ・サーディーンさんの納得できる意図をもってそう指導をされているのか、それとも形式的にもしくは思い込みでそのような指導をされているのかということで随分と意味が違ってくると思います。
なお、昨日の私の書き込みで
「授業の中で「どっちでも良い」と明言していただきたいものだと」
としたのは間違いでした。
ここは
「テストではどっちでも良い事にして欲しい」
とすべきところを、筆が滑ってしまいました。
ゴルゴ・サーディーンさん、コメントありがとうございます^^
「テストではどっちでもいい」と言うのが本当な気がします。
所詮、2数しかないので、その順番で理解をはかることそのことそのものが難しいです。
望ましいとされる掛け算の順番で書いているから理解しているとも言い難いです。
単純な採点基準と化してしまっていることもありそうですが…
ただ掛け算の順番を重視する指導者がいるということも事実ですので、そのことに関しては子供たちには私は伝えています。
お伝えしたい事は、おおよそ伝わったように思います。
ありがとうございました。