かけ算の決まりを利用して二桁×一桁を計算する時の教え方は？

小学校2年生で習う二桁×一桁の計算。

もうしばらくすると掛け算の筆算を習うのですが、この単元では掛け算の筆算はまだ使わずに解きます。

「かけ算の決まり」という単元の目的としては、数がどんな風にできているのかということを理解することでしょうか。

もちろん、掛け算の筆算を習っていれば掛け算の筆算で解くことができます。

筆算でも答えはあってしまうのですが、ここはただ解くことを問題としてみるのではなく、数の性質などがつかめるように筆算を使わずに解くことができるようになるといいですね。

途中式にこだわりすぎると、前の問題や例題などの式に当てはめて解くだけとなりがちなので、作業にしないのがポイントです。

1つ1つの問題をしっかり理解しながら解けるようになると、後々にもいい影響がでるのではないでしょうか。

今回の記事では筆算を使わずに解く、二桁×一桁の計算について書いてみたいと思います。

「かけ算の決まり」を使って解く、二桁×一桁の計算の教え方は？

早速例題をみていきましょう。

\(18\times 3\)をするには、筆算を使わずに掛け算の決まりを使って答えを求めることができます。

掛け算の決まりを使って答えを求めてみる。

\(18\times 1\)は18が1つということです。
\(18\times 2\)は18が2つということです。
\(18\times 3\)は18が3つということです。

18が1つ増えるごとに、18ずつ増えるので、こんな感じになります。
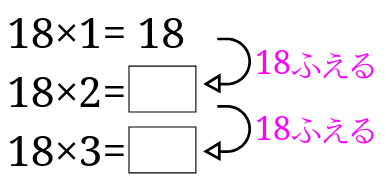と、いうことは･･･
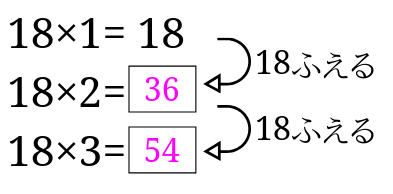となるので、答えは54となります。
順番に掛け算の性質を使って、18ずつ増やしていくとできますね。

足し算を使って求めてみる。

まずは掛け算の意味から、掛け算を足し算にします。
\(18\times 3\)は、18が3つという意味です。^[1]3が18個とも見ることができますが、計算が大変なので18が3つと見て解いていきます。
と、いうことは、18を3回足せばいいと言うことです。

つまり、\(18+18+18=54\)となり、答えは54となります。
足し算で解けるとはいっても、掛け算の意味がきちんと分かるのは大切ですよ。

・掛け算と足し算は同じように見えて違いがあるの？なぜどっちか使い分けるの？

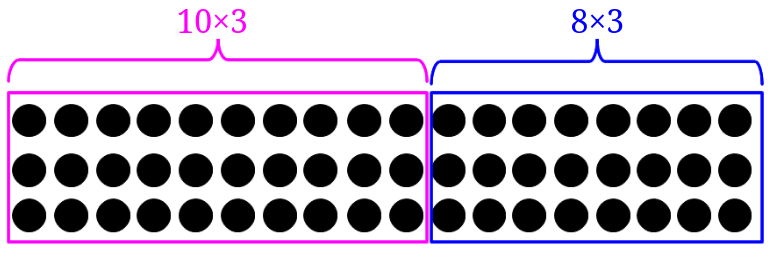
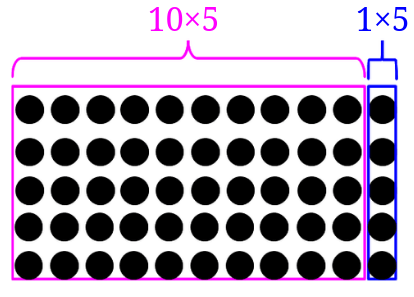
10と8に分けて考えてみる。

18を10と8に分けて考えてみましょう。
18が3つと言うことは、見方を変えると、10が3つと8が3つということになります。

それぞれ計算すると、
\(10\times 3=30\)
\(8\times 3=24\)
と、なります。これらを合わせて答えは54となります。

計算式だけ見てもピンとこないかもしれませんね。
ちょっと図に書き出してみると分かりやすくなります。
お子さんって数式だけだと、よく分からないことがあります。
ちょっと味気ない黒丸の図ですが、実際にするときはもっと遊び心を持ってすると良いと思います。

それではもう1題例題を解いてみましょう。

掛け算の決まりを使って解く！

もう一度、掛け算の決まりを使って解きます。
11ずつ増えるので、こんな感じですね。
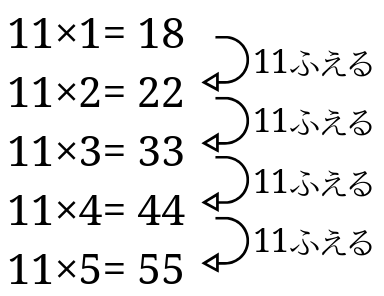足し算で解く！

11が5こなので、11を5回足しましょう。
\(11+11+11+11+11=55\)

10と1に分けて解く！

10と1に分けて考えると、11が5つは、10が5つと1が5つと考えられるので、

練習問題

次の問題を計算しましょう。
1、\(14\times 3\)
2、\(10\times 4\)
3、\(12\times 4\)
4、\(16\times 3\)
5、\(11\times 8\)
6、\(15\times 3\)
7、\(19\times 2\)
8、\(17\times 5\)
9、\(11\times 9\)
10、\(15\times 6\)

解答

1、\(42\)
2、\(40\)
3、\(48\)
4、\(48\)
5、\(88\)
6、\(45\)
7、\(38\)
8、\(85\)
9、\(99\)
10、\(90\)

まとめ

今回の記事では、筆算を使わない二桁×一桁の計算をしてみました。

計算そのものはそんなに難しくないかもしれません。
計算をすることそのものを目的とするというよりも、数字がどういう風にできているのかを理解する道具だと考えて教えてあげるといいのではないでしょうか。
この問題であれば筆算を教えてしまえば解けてしまいます。
しかし、目先ばかりを考えた解き方をしていくと、どこが分からないのかが不明確な状態でつまずいてしまうこともあります。
例えば12が10と2でできてるなんて、どうでも良いことのように見えますが、このことを理解したり、実感を持ったりということは後々役に立つと思いますよ。

少しずつ数に関する感覚も養っていけるといいですね。