分数の計算って小学生にとっては難しいですよね。
分数そのものが意味するところをきちんと理解するのも大変ですし、さらに計算となると苦手だと感じる小学生が多いのではないでしょうか。
今回の記事では、約分のない分数の掛け算について書いてみたいと思います。
約分のない分数の掛け算のやり方は?
それでは早速例題をみていきましょう。
(1)\(\frac{1}{2}\times \frac{3}{4}\)
(2)\(\frac{4}{5}\times \frac{7}{9}\)
分数の掛け算は、そんなに難しくありません。
分子は分子同士、分母は分母同士を掛ければOKです。
例題の(1)をみていきましょう。
分子は分子同士、分母は分母同士を掛ければいいので、
\(\frac{1}{2}\times \frac{3}{4}=\frac{1\times 3}{2\times 4}\)
となります。
あとは分子と分母をそれぞれ計算をしたら出来上がりです。
\(\frac{1}{2}\times \frac{3}{4}=\frac{1\times 3}{2\times 4}=\frac{3}{8}\)
となります。
分数の掛け算は、分数の計算の中では最もやりやすい計算です。
分数の掛け算ができないと、分数の割り算もできないのできちんとできるようにしておきたいところです。
例題の(2)も解いてみましょう。
分数の掛け算を計算するには、分子は分子同士、分母は分母同士を掛ければOKでした。
この問題も同じようにすれば解けます。
(2)\(\frac{4}{5}\times \frac{7}{9}=\frac{4\times 7}{5\times 9}=\frac{28}{45}\)
となります。
やり方も覚えやすいと思うので、計算にもある程度慣れておくといいかもしれませんね。
分数の掛け算ってどういう意味?
計算をしていて、\(2+3\)のような計算であればまだイメージができるものの、分数や小数になると途端にイメージするのが難しくなります。
今回の分数の計算を目で見える形にしてみましょう。
先ほどの例題の(1)を使って考えてみましょう。
(1)\(\frac{1}{2}\times \frac{3}{4}\)
まずは、下のような長方形をもとに考えてみます。

まずは下の長方形を\(\frac{1}{2}\)にしてみましょう。


これに、\(\frac{3}{4}\)を掛けるので、今度は横向きに4等分にしてみましょう。
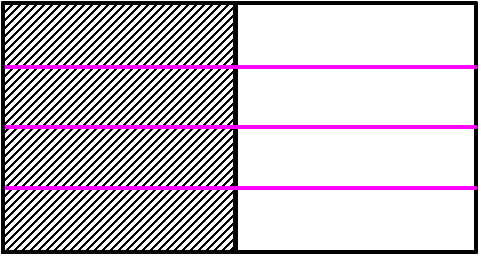
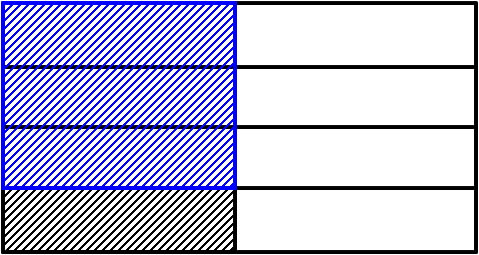
\(\frac{3}{4}\)なので、青い四角で囲んだところが答えということになります。
練習問題
次の計算をしましょう。
1、\(\frac{3}{4}\times \frac{1}{2}\)
2、\(\frac{7}{8}\times \frac{5}{2}\)
3、\(\frac{1}{9}\times \frac{7}{2}\)
4、\(\frac{5}{6}\times \frac{1}{3}\)
5、\(\frac{2}{5}\times \frac{3}{5}\)
解答と解説
やり方はどの問題も同じです。
分子は分子同士、分母は分母同士を掛ければOKです。
1の解説
\(\frac{3}{4}\times \frac{1}{2}=\frac{3\times 1}{4\times 2}=\frac{3}{8}\)
2の解説
\(\frac{7}{8}\times \frac{5}{2}=\frac{7\times 5}{8\times 2}=\frac{35}{16}\)
3の解説
\(\frac{1}{9}\times \frac{7}{2}=\frac{1\times 7}{9\times 2}=\frac{7}{18}\)
4の解説
\(\frac{5}{6}\times \frac{1}{3}=\frac{5\times 1}{6\times 3}=\frac{5}{18}\)
5の解説
\(\frac{2}{5}\times \frac{3}{5}=\frac{2\times 3}{5\times 5}=\frac{6}{25}\)
まとめ
今回の記事では、分数の掛け算について書いてみました。
分数の計算の中でも、分数の掛け算の計算はしやすい計算になります。
この後約分ができる分数の掛け算になるので、ここはすんなりできるようにしておきたいですね。
さらに、後に習う分数の割り算のもとになるので、まずは掛け算をスラスラできるようにはしておきましょう。




