長方形の面積から辺の長さを求める問題の解き方

長方形の面積を求める問題はそんなに難しくないというお子さんがほとんどではないでしょうか。

一方で、面積が与えられている状態から辺の長さを求めるというのは、イメージがしづらくなるため苦手とするお子さんが随分と増えます。

今回の記事では、長方形の面積が与えられた時の1辺の長さの求め方について書いてみたいと思います。

長方形の面積から辺の長さを求めるには

それでは例題を使って実際に解き方をみていきましょう。

例題1

長方形の□に当てはまる数を求めましょう。

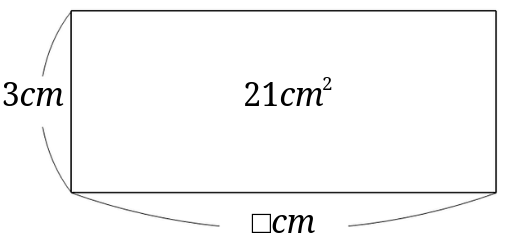
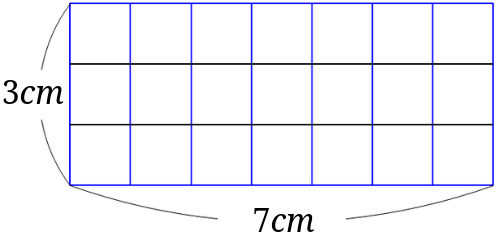
縦の長さが\(3cm\)、面積が\(21cm^2\)で、横の長さが分からない長方形です。
解き方は、面積を縦の長さが割ることで求めることができます。
つまり、この例題の場合は、$$21\div 3=7$$となり、求める長方形の横の長さは\(7cm\)となります。

長方形の面積が分かっていて、縦の長さと横の長さの一方が分からないときの求め方はこんな感じになります。

公式として書き出してしまうとなんてことはありません。
しかし、あらかじめこのことをすればいい、と分かっていれば易しいのですが、そうでなければ結構難しく感じてしまうお子さんが多くなります。
そのため、できればきちんと何をしているのかまで理解しておくことがお薦めです。

長方形の面積を縦や横の長さで割るともう一方の辺の長さが求められる理由

先程の例題をもう一度使って説明しますね。
長方形の面積は縦の長さと横の長さをかけることで求められます。
まずはこの意味を押さえておくと理解しやすくなります。

面積は\(cm^2\)と表しますが、\(1cm^2\)は一辺が\(1cm\)の正方形の面積です。
\(1cm^2\)は、一辺が\(1cm\)の正方形であることを頭に置きながら考えてみましょう。
例題の長方形は縦の長さが\(3cm\)、面積が\(21cm^2\)です。
ということは、この長方形は、一辺が\(1cm\)の正方形がたてに3列並んで、その正方形が全部で21個あると分かります。

21を3で割ることで、1列に一辺が\(1cm\)の正方形が並んでいるのかということを求めることができます。
この場合は\(21\div 3=7\)となるので、1列に7つの一辺が\(1cm\)の正方形が並んでいるということが分かります。

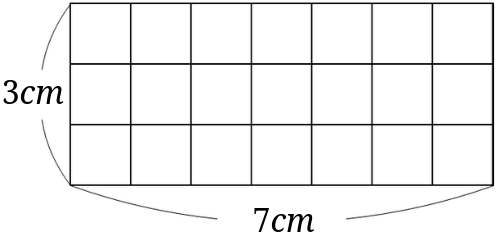
横の長さは、横に並んだ一辺が\(1cm\)の正方形の数と等しいので^[1]一辺の長さが\(1cm\)なので、\(1cm\times\)一辺が\(1cm\)の正方形の数となります。、この長方形の1辺の長さは\(7cm\)となります。

なぜ面積を一辺の長さで割ると他の一辺の長さが求められる？

\(21\div 3\)をすると横の長さが求められる理由がピンと来ないときには割り算の理解が浅いことがあります。
そんなときはもう少し詳しく説明してあげる必要があります。

考え方①(等分除的に考えると)

\(21\div 3\)を、「21を3等分すること」と考えると、3等分した1つ分は7ということになります。
つまり、たてに3列で並べると横に7つ一辺が\(1cm\)の正方形が並ぶということが分かります。
横に7つ･･･ということは、横の長さは\(7cm\)となります。

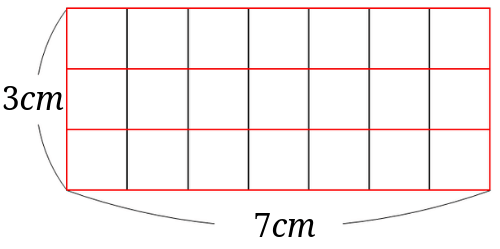
考え方②(包含除的に考えると)

たてに3つずつ一辺が\(1cm\)の正方形を並べることを考えてみます。
すると、横に1列並べるごとに、一辺が\(1cm\)の正方形が3つ必要になります。
見方を変えると一辺が\(1cm\)の正方形が3つあるごとに横は1列増えるということが分かります。
つまり21には3の塊が7つあるので、横に7列並ぶことになることから、横の長さが\(7cm\)と判断することができます。

まとめ

長方形や正方形の面積が与えられた時の1辺の長さの求め方について書いてみました。
なんとなく長方形の面積を与えられた長さで割ればいいと考えても答えは出せるかもしれません。
しかし、習ってからある程度時間がたってしまうと、面積と一辺の長さをかけてみたり、足してみたりと、好き放題するお子さんもでてきます。
きちんとした理解をしておかないとどうしても、公式だらけになってしまい混乱しがちです。
なぜ、割ることで分からない一辺を求めることができるのかが分かっていると、スムーズに勉強をすすめられると思います。
・面積のまとめへ戻る