正方形・長方形の面積が求められるようになったら、次は平行四辺形の面積の求め方です。
平行四辺形の面積の公式から、公式がそうなる理由まで解説します。
平行四辺形の面積の公式
まずは平行四辺形の面積の公式からみていきましょう。
平行四辺形の面積\(=\)底辺\(\times\)高さ
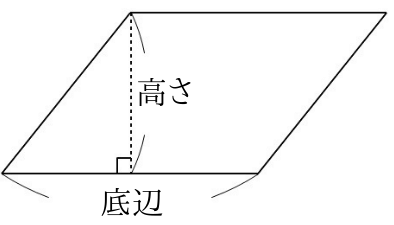
平行四辺形の底辺と高さはこんな感じですね。
注意すべきは高さは、底辺に垂直になることです。
それでは公式を実際に使ってみましょう。
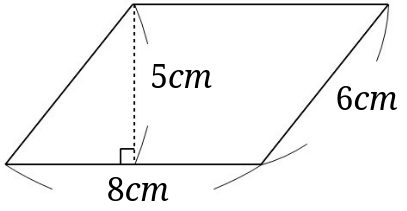
平行四辺形の面積は、底辺\(\times\)高さでした。
底辺の長さが、\(8cm\)というのは簡単に分かると思います。
次に高さを考えましょう。
ここがポイントです!
この図の\(6cm\)のところを、つい高さにしてしまうお子さんがいますが、高さは底辺に垂直なところになります。
底辺に垂直なところが高さになるのは後ほど解説します。
つまり、この平行四辺形では、高さは底辺に垂直な\(5cm\)のところとなります。
平行四辺形の面積は、\(8\times 5=40\)となります。
よって、この平行四辺形の面積は\(40cm^2\)となります。
平行四辺形の面積の公式が、底辺×高さとなるのはなぜか
平行四辺形の面積の公式が底辺\(\times\)高さになる理由をみていきましょう。
先ほどの平行四辺形を切り貼りしてみましょう。
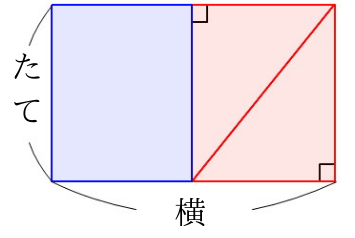
下の図のように、2つの直角三角形と長方形に分けてみます。
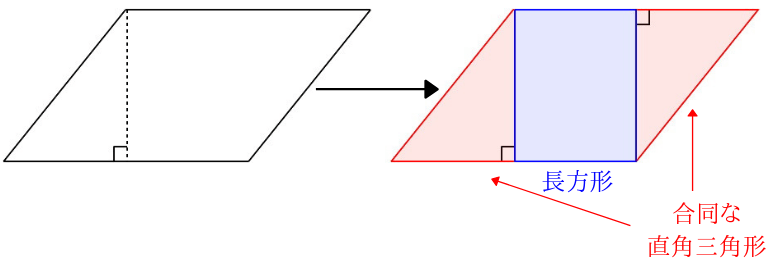
2つの直角三角形は合同です。
次にその一方の直角三角形を移動させてみます。
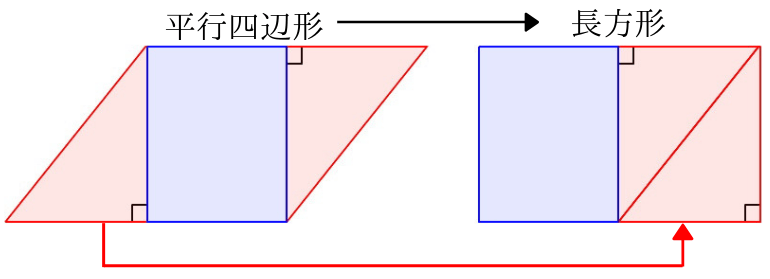
直角三角形を移動させてみると、平行四辺形が長方形になりました。
と、いうことは、平行四辺形の面積を求めるには、この長方形の面積を求めればいいということになります。
長方形を求めるには、縦×横をすればでてきます。
また、もとの平行四辺形の底辺と高さを書き入れてみます。
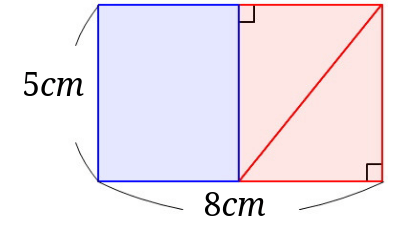
底辺と横は見た目で一致していることが分かります。
また、縦と高さの位置が一致しています。
つまり、このことから、平行四辺形の面積を求めるには底辺×高さをすればいいと分かります。
三角形を切り取って平行四辺形を長方形にできないときはどうしたらいい?
三角形を切り取って平行四辺形を長方形にできない平行四辺形とは下のような平行四辺形です。
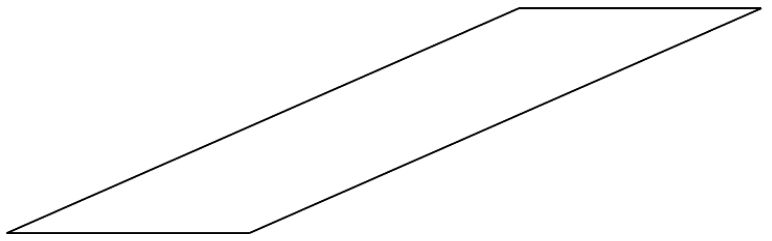
こんな形の平行四辺形だと、うまく長方形にできないため「平行四辺形の面積=底辺×高さ」ということをイメージしづらくなってしまいます。
この場合は少し視点を変えて考えてみるとうまくいきます。
今までのような面積の求め方とは見方を変えて、全体の面積から余分な面積を差し引いて、平行四辺形の面積を出してみます。
まずは平行四辺形を含む長方形を書いてみましょう。
下の図のようになればOKです。
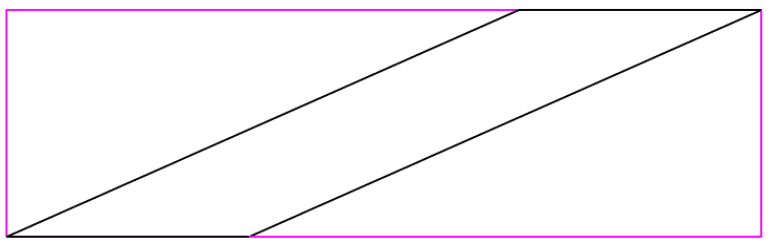
長方形を作ることで、2つの直角三角形ができました。
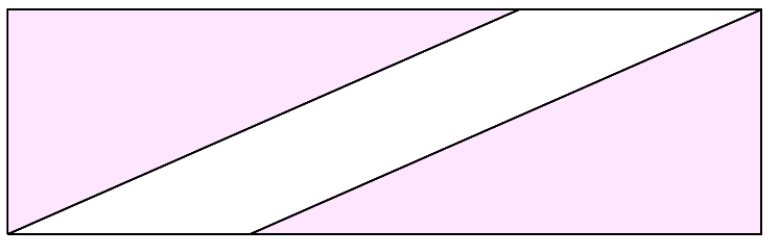
この長方形の面積ははじめの平行四辺形に2つの直角三角形を足したものです。
このことを平行四辺形を中心に考えると、長方形の面積から2つの三角形の面積を引いたものだと分かります。

長方形から三角形2つの面積を引けば平行四辺形の面積になることは分かったので、今度は三角形の場所を変えてみます。
右側にある三角形を左側に寄せてみます。
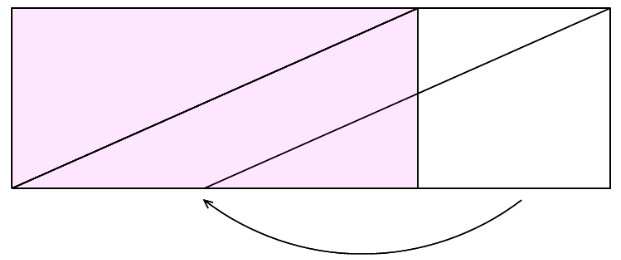
このとき、残った右側の長方形(正方形っぽくもみえますが)の面積は、長方形から2つの三角形を引いた面積です。
と、いうことは、この長方形の面積ともとの平行四辺形の面積は等しいということになります。
またこの長方形の縦の長さは平行四辺形の高さに、横の長さは底辺に当たります。
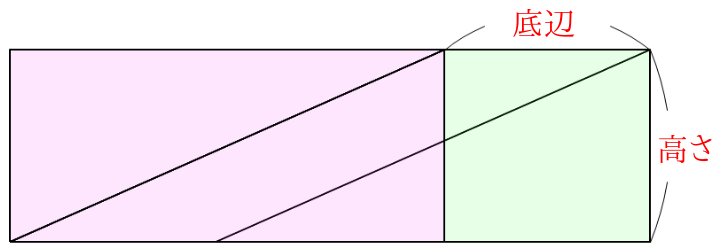
このことから、「平行四辺形の面積=底辺×高さ」と、いうことがいえます。
先に説明した平行四辺形の面積の説明も、この長方形から2つの三角形を差し引くという形で説明可能です。
ただ、直接面積を求める形ではないので、少し分かりにくいということもあるかもしれません。
そんなときは、図を中心に説明してあげるといいと思います。
まとめ
平行四辺形の面積の公式や公式が底辺×高さになる理由を説明してみました。
平行四辺形の面積を求めるだけであれば、底辺×高さだと覚えておけば困ることは少ないと思います。
しかし、平行四辺形を長方形に変えることで、長方形と同じように面積が求められることが分かれば、平行四辺形の底辺と高さの関係が直角ということも納得がいくのではないでしょうか。
もしお子さんが斜めの辺などを掛けてしまう場合などには面積の公式の理屈がしっかり分かると良いかもしれません。
周り道に見えますが、平行四辺形を長方形に変えることができるイメージを持っていると公式も忘れることも少なくなります。
・面積のまとめへ戻る




