長方形や正方形の面積は、公式を覚えておしまいとなりがちです。
きちんと意味が分かると面積の理解が深まり、公式という認識なしに面積を求められるようになります。
今回の記事では、長方形や長方形の面積の公式がなぜこのようになっているのかについて書いてみたいと思います。
正方形の面積の求め方は?
長方形は「たて×よこ」、正方形は「一辺×一辺」で面積を求めることができます。
なぜ、このような公式で求めることができるのか考えてみましょう。
まずは、面積の基準についてみていきます。
面積の単位の基準である\(1cm^2\)は、一辺が\(1cm\)の正方形の面積です。
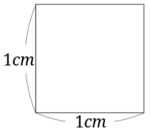
上の図を基準に考えると、長方形や正方形の面積の求め方を容易に理解することができます。
それではこのことを利用して例題を解いてみましょう。
正方形の面積の公式の意味
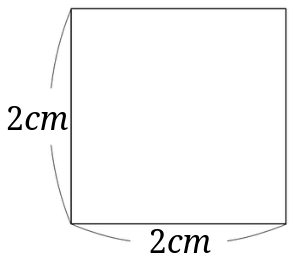
まずは公式を使って求めてみましょう。
正方形の面積の公式は「一辺×一辺」なので、$$2cm\times 2cm=4cm^2$$となります。
公式にそのまま入れただけなので、なんてことないですね。
次に公式を使わずにこの正方形の面積を求めてみましょう。
この正方形を一辺が\(1cm\)の正方形に分けてみましょう。
分けてみると、下の図のようになります。
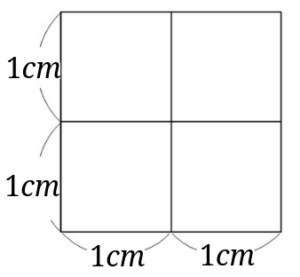
先程の正方形の中に1辺が\(1cm\)の正方形が4つあることが分かります。
1辺が\(1cm\)の正方形の面積は\(1cm^2\)です。
1辺が\(1cm\)の正方形が4つあるので、この正方形の面積は\(4cm^2\)ということが分かりました。
正方形の面積の公式を導くには
1辺が\(1cm\)の正方形がいくつあるのかを数えることである正方形の面積を求めることができました。
正方形のなかにいくつ1辺が\(1cm\)の正方形があるのかを考えると正方形の面積の公式を導くことができます。
1辺が\(2cm\)の正方形なので、1辺が\(1cm\)の正方形が縦に2列、横に2列並んでいることが分かります。
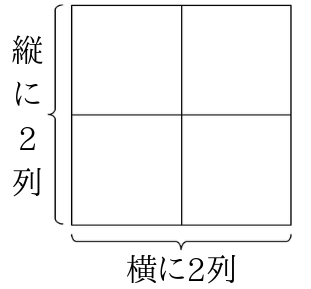
このことから「一辺×一辺」をすることで、正方形の中にいくつ1辺が\(1cm\)の正方形があるのかが分かります。
その1辺が\(1cm\)の正方形の個数が面積になるので、正方形の面積は「一辺×一辺」だということが分かりました。
長方形の面積の求め方
次の例題で長方形の面積を求めてみましょう。
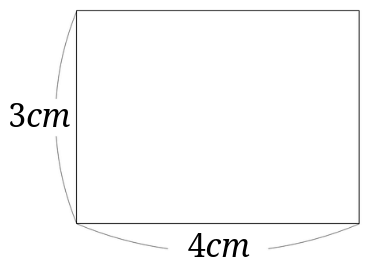
縦の長さが\(3cm\)、横の長さが\(4cm\)の長方形です。
長方形の面積の公式は、「縦×横」なので$$3cm\times 4cm=12cm^2$$となります。
この長方形の面積を公式を使わずに求めてみましょう。
この長方形を一辺が\(1cm\)の正方形に分けてみます。
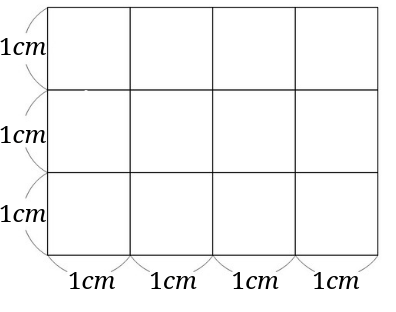
すると先程の長方形の中に1辺が\(1cm\)の正方形が12個あることが分かります。
1辺が\(1cm\)の正方形の面積は\(1cm^2\)です。
つまり、この長方形の面積は\(12cm^2\)ということが分かりました。
長方形の面積の公式の意味
1辺が\(1cm\)の正方形の数を数えることで長方形の面積が分かりました。
少し見方を変えると、長方形の面積を求めるには、長方形の中に1辺が\(1cm\)の正方形がいくつあるのかを数える、求めることができればいいということになります。
縦の長さが\(3cm\)、横の長さが\(4cm\)の長方形には、1辺が\(1cm\)の正方形が縦3列、横4列並んでいるということです。
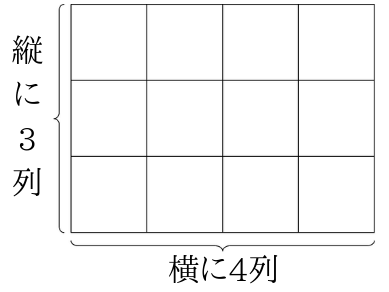
つまり、長方形の中にある1辺が\(1cm\)の正方形の正方形の個数は「縦×横」で求めることができるので、長方形の面積の公式は「縦×横」と分かります。
長方形も正方形の面積の求め方は同じ?正方形の面積はたて×よこではだめ?
長方形と正方形の面積の求め方を解説しました。
公式としては、「長方形の面積=たて×よこ」、「正方形の面積=一辺×一辺」と区別されていますが、結局やっていることは同じです。
長方形の面積を求める場合も長方形の面積を求める場合も、区別する必要はありません。
「長方形の面積=たて×よこ」だけで、長方形や正方形の面積を求めることができます。
まとめ
今回の記事では、長方形や長方形の面積の公式がなぜこのようになっているのかについて書いてみました。
面積の1番の基本的な事項は、\(1cm^3\)が一辺が\(1cm\)の正方形の面積ということです。
まずは基準を理解することが大切です。
このことから、正方形の面積を求める公式が「一辺×一辺」であることや、長方形の面積を求める公式が「縦×横」であることは理解することができます。
面積を求めるだけであれば、公式を単に暗記してしまえば求めることができますが、今後でてくる面積の公式、求め方への理解はずいぶんと違ってきます。
・面積のまとめへ戻る