時速○kmを秒速 △mにする裏技やその逆の便利な速さの公式って？

速さの単位を変えるのって結構面倒なものです。

例えば時速60kmを時速〇mにする、時速60kmを分速△kmにするような場合はそんなに手間にならないのですが、時速〇kmから秒速△mのように時速から秒速、kmからmのように2カ所が変わると結構面倒なものです。

今回の記事では、その中でも、特に時速〇kmから秒速△mの単位換算の裏技について書いてみたいと思います。

時速○kmを秒速 △mに直す裏技を紹介

時速○$km$を秒速△$m$に直すのはちょっとめんどくさいですよね。
知っておくと便利な裏技があるのでご紹介します。

例題1

時速$36km$は秒速何$m$ですか。

時速$36km$を秒速△$m$に、単位を変換する問題です。
時速○$km$を秒速 △$m$に直す時にはこんな裏技があります。

MEMO

時速○$km$から秒速△$m$にするには、3.6で割る

つまり、時速$36km$なので、36を3.6で割ります。$$36\div 3.6=10$$となるので、答えは秒速10$m$ということになります。
とても簡単に求めることができましたね。

なぜ時速○$km$を秒速△$m$にするときは3.6で割るの？

時速○$km$の$km$を$m$にしてみると、時速○$\times 1000m$となります。
さらに、時速を秒速にするには、3600で割れば良いので、秒速○$\times 1000\div 3600m$となります。
さらに計算すると秒速○$\div 3.6m$となり、時速○$km$を秒速△$m$にするには3.6で割ればいいということになります。

秒速△mを時速○kmに直すにはどうしたらいいの？

それでは逆の場合にはどうすれば良いのでしょうか。
例題1の時速○$km$を秒速△$m$にするには、3.6で割ることで求めることができました。
と、いうことは、秒速△$m$を時速○$km$にするには、3.6を掛けることで求められます。
・時速から分速のような時間の単位だけでなくkmからmの距離の単位まで速さの単位変換ができるようになろう！

試しにやってみましょう。

例題2

秒速$20m$は時速何$km$ですか。

先程の例題1とは逆で3.6を掛けることで求めることができます。$$20\times 3.6=72$$となり、時速$72km$ということになります。
知っていると、簡単に求めることができますね。

MEMO

秒速△$m$から時速○$km$にするには、3.6を掛ける

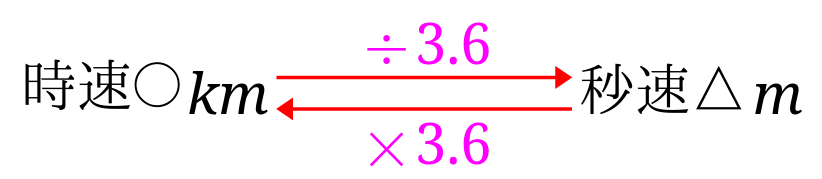
秒速△$m$を時速○$km$にするには3.6を掛けるの？

秒速△$m$を時速○$km$にするには、なぜ3.6を掛けるのかについて考えてみましょう。
まずは秒速△$m$の$m$を$km$にしてみましょう。
すると、秒速△$\div 1000km$となりました。
さらに秒速を時速にするには3600倍すればいいので、秒速△$\div 1000\times 3600km$となります。
計算して、秒速△$\times 3.6km$となるので、秒速△$m$を時速○$km$にするには3.6を掛ければいいということが分かりました。

「秒速△$m$から時速○$km$にするには、3.6を掛ける」、「時速○$km$から秒速△$m$にするには、3.6で割る」ということって覚えるべき？

「秒速△$m$から時速○$km$にするには、3.6を掛ける」、「時速○$km$から秒速△$m$にするには、3.6で割る」ということを、覚えて問題を解けば早く計算ができるようになり、時間短縮になりそうです。
もちろん、覚えてきちんと使いこなせるのであれば、という条件付きではありますが。

現実的には公式が増えて混乱してしまう、もしくは公式が多くて混乱してしまっているということもあると思います。
この公式は、覚えなくても効果的に使う方法もあります。
ちょっと見方を変えると計算の工夫のような感じで早く問題を解くことができます。

先ほどの例題を使ってやってみましょう。

例題1

時速$36km$は秒速何$m$ですか。

多くのお子さんがやる方法で最初にしてみます。
まずは時速36$km$を時速〇$m$に直します。
$36\times 1000=36000$
これで時速$36km$は時速$36000m$ということが分かりました。

時速$36000m$を分速〇$m$になおします。
$36000\div 60=600$

分速$600m$を秒速〇$m$にします。
$600\div 60=10$
となり、答えは秒速$10m$となります。

ちょっと計算が面倒ですね。

ちょっとうまく計算してみましょう。

工夫して計算してみよう

先ほどの単位換算の流れは、

時速$36km$→時速$36000m$→分速$600m$→秒速$10m$でした。

同じように計算の流れをみてみると、

$36\times 1000=36000$
$36000\div 60=600$
$600\div 60=10$
長くて面倒ですね。

この計算過程を途中で計算せずに、まとめて計算するととても楽に計算することができます。
この計算の流れを1つの式にしてみると、$$36\times 1000 \div 60\div 60$$となります。

この計算を後ろの3つの項からやってみましょう。
$1000\div 60 \div 60$からということです。
まずは、0を消して、
$10\div 6 \div 6$
となりました。

これを計算すると…3.6
あとは$36\div 3.6$でできあがりです。

「時速○$km$から秒速△$m$にするには、3.6で割る」の3.6がでてきましたね。
公式として覚えなくても、簡単に出せました。

計算の順序などをうまく工夫できるようになるといいと思います。

まとめ

時速〇kmから秒速△mの単位換算の裏技について書いてみました。
時速〇kmから秒速△mの単位換算ができればこの逆の「秒速△$m$を時速○$km$にする」ということはそんなに難しくないと思います。
便利な公式として覚えるととても早く計算ができるので、時間短縮にはなかなか効果的かもしれません。
ただ、公式が増えるという意味では、このことを覚えて混乱してしまうという場合には無理に覚えて使うと言うことは避けた方がいいでしょう。
そんなときは、「秒速△$m$から時速○$km$にするには、3.6を掛ける」、「時速○$km$から秒速△$m$にするには、3.6で割る」ということが分かるようにようになる、導けるようになるといいと思います。
慣れてくれば、一瞬で導けるようになりますよ。