分数の割り算を習うあたりででてくる言葉に「逆数」という言葉があります。
なんとなく、分母と分子をひっくり返した数と習うことが多いものです。
今回の記事では逆数って、なんなのかということについて書いてみたいと思います。
▼他にも見ておきたい小数・分数のつまずきポイントについて▼
分数や小数の単元で小学生がつまずきやすい主なポイントとは?
分数や整数や小数の逆数の取り方がわからない時の教え方や意味の考え方って?0の逆数って?
逆数とはそもそも何なの?
まず逆数にするにはどうすればいいのかを考える前に大切になってくるのが、逆数って何のなのかということ。
なんとなく分母と分子を入れ替えた数が逆数と思っているお子さんってたくさんいます。
実際、分数の割り算では基本的に、分数の分子と分母を入れ替えた数と考えてもうまく計算することができます。
それでは例題を扱いながら、逆数についてみていきましょう。
$$(1)\frac{2}{3} (2) \frac{7}{3}$$
(1)から順番にみていきましょう。
分数の分母と分子を入れ替えた数と考えると、(1)の逆数は、\(\frac{3}{2}\)となり、(2)の逆数は、\(\frac{3}{7}\)となります。
別になんてことはありませんね。
それでは次のような場合はどうでしょうか。
$$(1)2 (2)\frac{1}{3}$$
困ったことに(1)をみてみると、整数である2です。
分母がないときの逆数はどうしたらいいの?
分子と分母があるときの逆数は分子と分母を入れ替えればよかったのですが、今回は困りました。
分母が見当たりません。
こんな時は、2を\(\frac{2}{1}\)とみて、分子と分母を入れ替えてもいいのですが、ちょっとお子さんに教えてみると、意外としっくり来ないことが多いです。
やはり逆数という言葉から分子と分母を入れ替えるものというイメージが先行してしまうため、整数や小数の場合のような分母が見当たらない場合に逆数が何かピンと来ないということが多くあります。
逆数は、「分子と分母を入れ替えた数」という認識ではなく、「その数に掛けると1になる数」と理解する方が逆数を扱いやすくなります。
(1)では「2に掛けると1になる数」は何?という具合に考えると、\(\frac{1}{2}\)というのは容易に分かるのではないでしょうか。
次に(2)\(\frac{1}{3}\)の逆数を考えてみましょう。
\(\frac{1}{3}\)に掛けると1になる数と考えると3ということはすぐに分かるのではないでしょうか。
この時に逆数を分子と分母を入れ替えた数という認識のまま考えると、お子さんは\(\frac{3}{1}\)と答えに書きがちです。
もちろん誤りとまでは言えないと思いますが、学校のテストでは減点が免れないのではないでしょうか。
逆数はその数に掛けると1になる数と考えると、分かりやすくなりますよ。[1]そもそも逆数はこういった意味なので、掛けると1になる数と理解してもらいましょう。中学生になってからも使えますよ。
$$(1)0.12 (2)0$$
(1)0.12の逆数から考えてみましょう。
小数の逆数ってどうすればいいの?
小数の逆数は、一旦分数に直すと、とても考えやすくなります。
0.12は\(\frac{12}{100}\)なので、0.12の逆数は\(\frac{100}{12}=\frac{25}{3}\)となります。
ここで注意したいのが、\(\frac{100}{12}\)と答えてしまうことです。
ついつい約分をすることなくこのまま解答としてしまう子が結構います。
きちんと約分までできるようするといいですね。
分数に直すのはめんどくさいという時は…
0.12を分数に直さずに考えてみましょう。
逆数は0.12に掛けて1になる数なので、\(\frac{1}{0.12}\)となります。
0.12に掛けてみると、
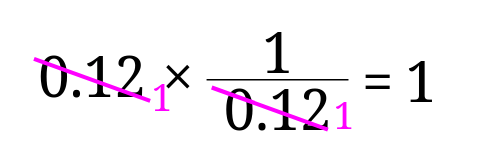
このままのほうが計算はしやすいのですが、答えとしては微妙な感じです。
分母が小数ですしね。
\(\frac{1}{0.12}\)の分母と分子を整数にしたいと思います。
まずは、分子と分母に100を掛けて、それから約分していきます。$$\frac{1}{0.12}=\frac{100}{12}=\frac{25}{3}$$となります。
こちらの方が入りは楽そうに見えますが、分数にしてから逆数を求めることと、そんなに大差はなさそうです。
分数の理解を深めるためには、小数を分母に入れてみるというのも悪くないと思います。
最後に(2)0の逆数を考えてみましょう。
逆数を分母と分子を入れ替えた数と考えていると、もっとも間違えやすいものかもしれません。
\(0=\frac{0}{0}\)[2]本当は違いますよと考えて0の逆数は\(\frac{0}{0}\)もしくは0と答えるお子さんがちょくちょくいます。[3]普通学校では聞かれないと思いますが、理解を深めるために私が聞いてみるだけです。役に立つかは…
逆数を分子と分母を入れ替えた数と考えると難しくなっちゃう例ですね。
逆数は、その数に掛けると1になる数でした。
0に掛けると、1になる数を考えてみると…
ありませんね!
0に何を掛けても0は0のままです。
つまり0の逆数は「なし」ということになります。
まとめ
今回の記事では逆数って、なんなのかということについて書いてみました。
逆数は、言葉からもしっくりくるせいか、分数の分母と分子を入れ替えた数というイメージを持っているお子さんが多くいます。
しかし、そのイメージで行くと整数や少数の逆数が分からない…ということにもなりやすいです。
そうならないように、きちんと逆数をその数に掛けると1になる数と理解しておけば、整数や小数の逆数も分かりやすくなります。
・分数や小数のまとめへ戻る




