面積の公式の中で、異色なものは台形の面積。
覚えたようですぐに忘れてしまいがちな公式ではないでしょうか。
台形の面積の公式を忘れても面積を出せるようにしてみたいと思います。
公式を使わない台形の面積の求め方って?
まずは台形の面積の例題を使って実際に求めてみましょう。
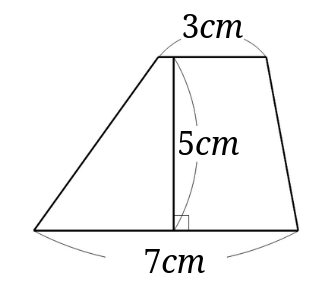
長方形などと比べると、上底や下底という見慣れない言葉が出てくるので忘れやすい公式です。
公式を忘れてしまったときや、覚えられないときは2つの三角形に分けて考えると台形の面積を求められます。
台形の対角線を利用した面積の求め方
台形の面積の公式を忘れてしまったときは、このやり方が王道ではないでしょうか。
単に台形の対角線を引き、2つの三角形に分けるだけで求められます。
2つの三角形に分けることができたら、三角形の面積をそれぞれ求めて足せば台形の面積になります。
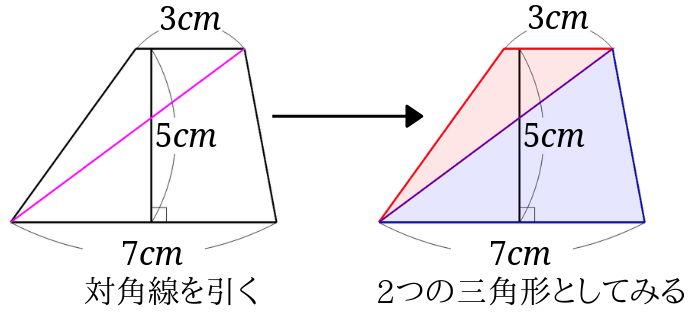
まずは赤い三角形の面積を求めます。
\(3\times 5\div 2 =7.5\)
さらに青い三角形の面積を求めます。
\(7\times 5\div 2= 17.5\)
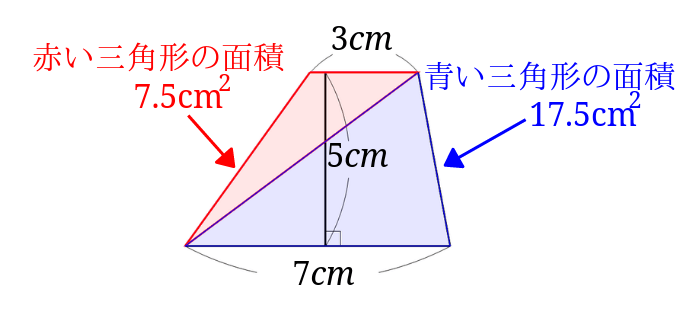
2つの三角形の面積を足すと台形の面積になります。
\(7.5+17.5=25\)
台形の面積の公式を使わずに面積を求めることができました。
この求め方であれば、台形の面積の公式を忘れてたとしても、すんなり求めることができます。
平行四辺形を用いる台形の面積の求め方
台形をひっくり返した図形ともとの台形とをくっつけると、平行四辺形ができます。
このことを利用しても、台形の面積を求めることができます。
台形をひっくり返したものを、下の図のようにくっつけてみます。
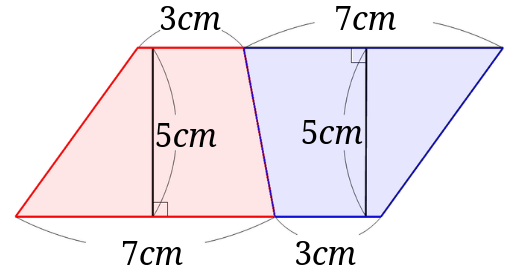
赤い元の台形と赤い台形をひっくり返した青い台形を合わせると、平行四辺形になっています。
平行四辺形として面積を求めるには、底辺×高さをすればいいですね。
底辺は、\(7+3\)で\(10\)となります。
高さは\(5\)なので、この平行四辺形の面積は、
\(10\times 5=50\)
この平行四辺形は、元の赤い台形2つ分の面積なので、平行四辺形の面積を2で割ります。
\(50\div 2=25\)
台形の面積を求めることができました。
等積変形を利用する台形の面積の求め方
最後に等積変形を使った台形の面積の求め方をやってみましょう。
その前に軽く等積変形について説明しておきます。
等積変形とは?
等積変形とは、面積を変えずに形を変えることを等積変形といいます。
ここでは三角形の等積変形を使います。
下の図のような三角形があるとします。
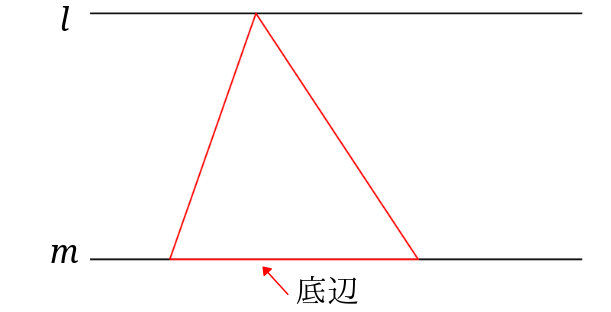
このとき三角形の底辺を共有し、直線\(l\)上にもう一つの角があるとき、面積を変えることなく、違う形の三角形に変えることができます。
ちなみに下に書いた三角形はみんな同じ面積です。
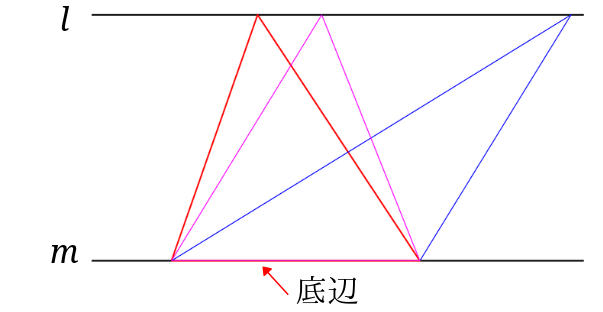
このことを利用して、台形の面積を求めてみましょう。
まず、等積変形をするために、下の図のように対角線を引きます。
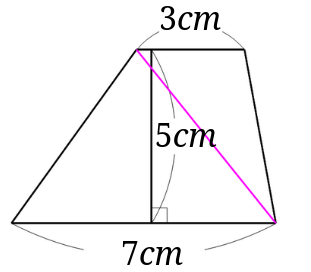
さらに引いた対角線と平行な直線を下の図のように書きます。
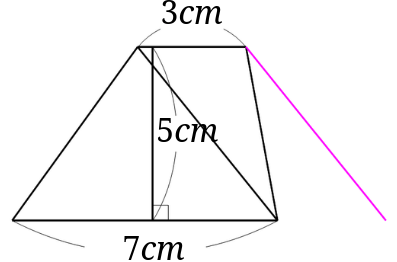
台形の下底を右に延長します。
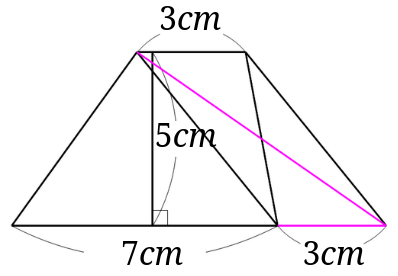 下の図の赤い三角形と青い三角形の面積は等しくなります。[1]等積変形がわかりにくいときは、赤い三角形も青い三角形も底辺\(3cm\)、高さ\(5cm\)の三角形とみてもいいと思います。
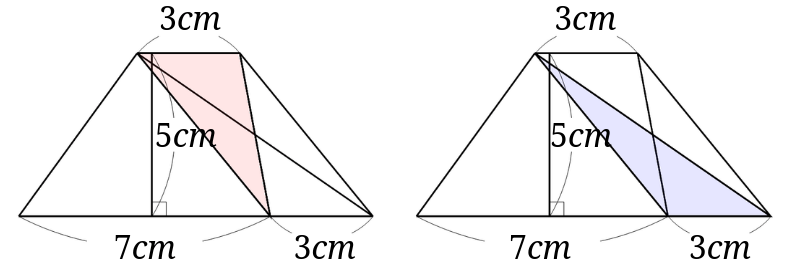
下の図の赤い三角形と青い三角形の面積は等しくなります。[1]等積変形がわかりにくいときは、赤い三角形も青い三角形も底辺\(3cm\)、高さ\(5cm\)の三角形とみてもいいと思います。
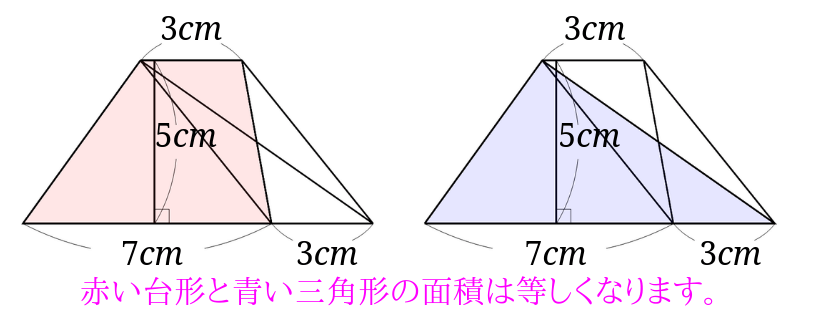
つまり、下の赤い台形の面積と青い三角形の面積が等しいので、台形の面積は青い三角形の面積を求めれば分かります。
 青い三角形の面積は、
青い三角形の面積は、
\( (7+3)\times 5\div 2=25\)
となり、求める台形の面積は\(25cm^2\)と分かりました。
まとめ
今回の記事では台形の面積を忘れてしまったり、覚えていないときの台形の面積の公式の求め方について書いてみました。
やり方そのものをみてみると、そんなに難しい方法ではないと思います。
しかし、小学生だと台形の面積を求めるには、台形の面積の公式を使わないといけないという偏見がかなり強いことが多いです。
そうでなくても、全く意味も分からず台形の公式に数字を入れて計算するだけというお子さんもたくさんいます。
このような過程でもきちんと面積が求められると分かると、算数で頭を使えるようになるきっかけになるかもしれません。
基本的には最初の台形を三角形2つに分けて求める方法が1番やりやすいと思います。
問題は、逆さまの三角形を認識できるかという点ですが、お子さんが理解できないときは図を回してあげると分かりやすいかもしれません。
台形を2つ合わせて平行四辺形にする方法は、台形の公式のイメージがしやすいので、こういう考え方もあると教えてあげるといいです。
最後の等積変形を使った方法は、お子さんが算数が好きというような場合には教えてあげてもいいかもしれません。
しかし、算数が苦手、嫌いというお子さんの場合は触れなくていいと思います。
・面積のまとめへ戻る
References
| ↑1 | 等積変形がわかりにくいときは、赤い三角形も青い三角形も底辺\(3cm\)、高さ\(5cm\)の三角形とみてもいいと思います。 |
|---|



