比例のグラフと比べると少し面倒なのが反比例のグラフです。
今回の記事では、反比例のグラフの書き方について書いてみたいと思います。
反比例のグラフの書き方
例題を使って反比例のグラフを書いてみましょう。
比例のグラフを書くときは原点ともう1点を定めて、その2点を直線で結ぶことでグラフを書くことができますが、反比例のグラフを書くには比例のグラフのように簡単には書くことができません。
まずは\\(x\)と\(y\)の関係を表にしてみましょう。
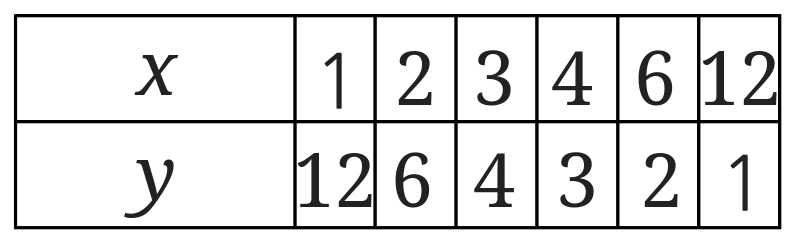
表を作る時のコツは\(x\)の値を1から順番に入れていくことです。
\(x\)と\(y\)の値が整数になる場合は必ずすべて書き込むようにします。
次に、その表を元にグラフに点を取っていきます。
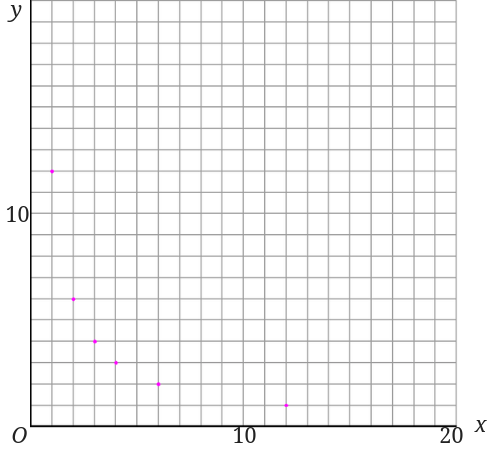
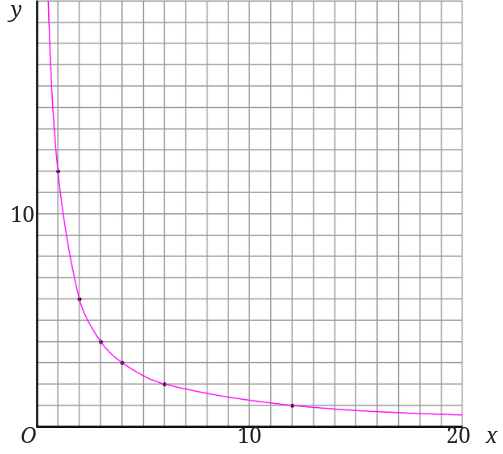
点を取ったら次に取った点を順番に結んでいきましょう。
この時に注意するのは絶対に定規を使ってはダメだということです。
必ずフリーハンドで、滑らかに点を結んでいくようにすれば大丈夫です。
反比例のグラフを書く手順をまとめると、
①反比例の式から表を作る
②表で出した点をグラフに取っていく
③グラフに取った点を滑らかな曲線で結ぶ
この手順でグラフを書くことができればOKです。
①の反比例の式から表を作るという手順は、1つ1つ計算して直接グラフに書き込んでもいいと思います。
反比例が苦手なお子さんの場合は一旦表にして、その点をグラフに落とし込んでいく方がやりやすいと思います。
注意した方がいい反比例のグラフの特徴
先程の「\(y=12\div x\)の\(x\)と\(y\)の関係を表すグラフ」を書く問題では整数で割り切れる点を取ってしまえば、問題になりませんでした。
反比例のグラフを書くときにあまり点が取れずどこを通せばいいのかはっきりしないこともあります。
また、点が少ないまま適当にグラフを書いてしまうと、減点になってしまったり、場合によっては不正解ということになってしまうこともあります。
そんな注意した方がいい反比例のグラフを書いてみましょう。
まずは先程と同じ手順で、まずは\(x\)と\(y\)の関係を表にしてみましょう。
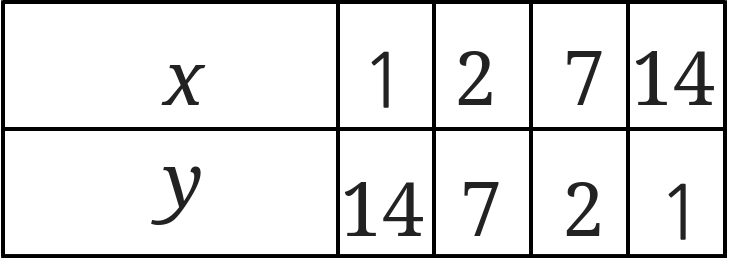
表が掛けたら座標をグラフに打ち込んでいきます。
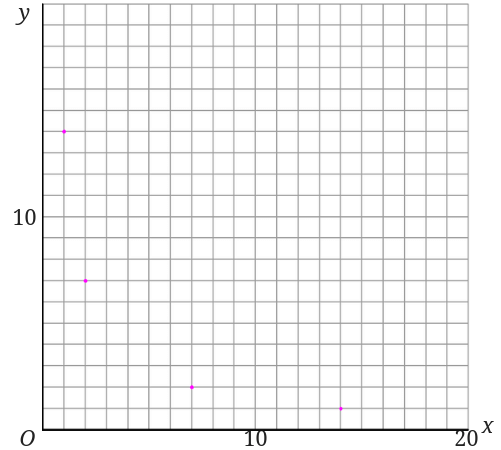
点を打ち込むことが出来たら、滑らかな曲線で結びます。
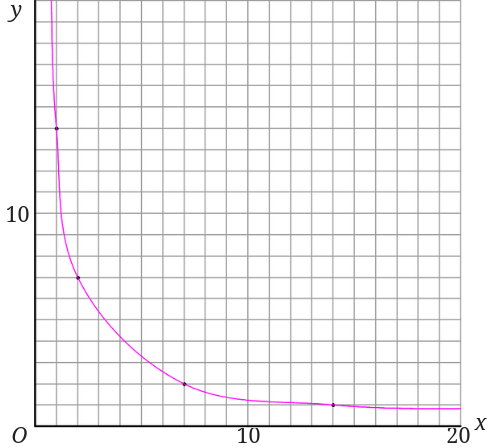
先程と同じ手順でグラフを書くことができました。
そんなに難しくありませんよね。
しかし、実はこのグラフには少しまずいところがあります。
どこかというと通るべき点を通っていないんです。
もう少し細かく表を作ってみます。
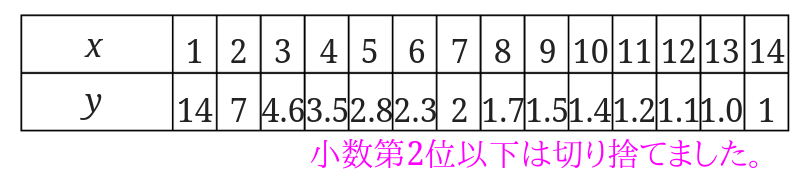
\(x\)に1~14までの整数を入れて計算してみました。
次にそれらの点を先程のグラフに追加して打ってみます。
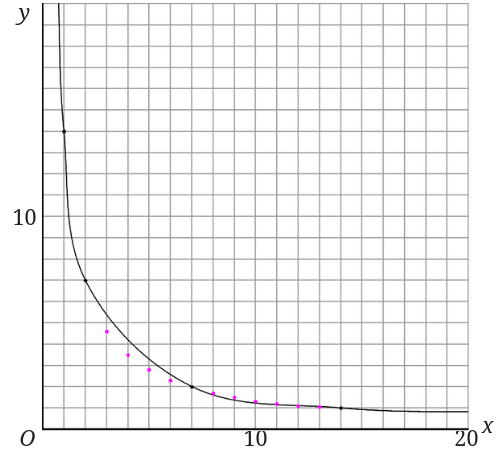
グラフに打った点を結んでみます。
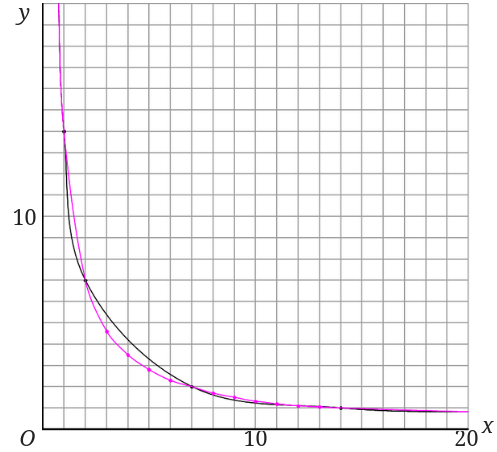 結構な誤差がありますね。
結構な誤差がありますね。
ただ、反比例のグラフはフリーハンドで滑らかに点を結んで曲線を書くため誤差がかなりでやすいグラフです。
多少の誤差は問題ないのですが、このグラフでは3箇所良くないところがあります。
その3箇所はに印を入れてみます。
\(x\)が3のところをみてみると、黒いグラフでは、5.4くらいでしょうか。
それに対してピンクのグラフでは、4.6くらいです。
この2つの点の誤差は0.8くらいあります。
ただ、この点がまずいのは誤差が大きいからという訳ではありません。
何が良くないのかというと、5より大きいのかそれとも小さいのかということがグラフから読み取れることです。
そうなると明らかに違うグラフと判断されてしまいます。
他の2点も同じ理由で、テストなどでは減点されてしまったり、不正解にされてしまうこともあるかもしれません。
方眼紙のようなものにグラフを書くときはなるべく多くの点を取ることがおすすめです。
逆に問題にならないのは、1.1を1.9くらいに書いたような場合です。こういう場合はそんなに問題になることはないと思います。
もちろんなるべく正確に書いた方がいいのですが、格子点をまたいでしまうと減点、不正解と扱われやすいので気を付けてください。
下のグラフの赤丸を入れたところはそれなりに誤差があります。(ピンクのグラフが正確かと言われると微妙ではありますが…)
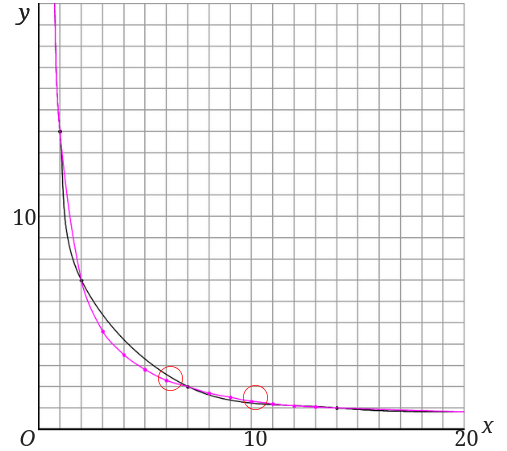 それなりに誤差があるように見えるのですが、格子点[1]\(x\)座標も\(y\)座標も整数の点をまたいでいないため許容してもらえると思います。
それなりに誤差があるように見えるのですが、格子点[1]\(x\)座標も\(y\)座標も整数の点をまたいでいないため許容してもらえると思います。
格子点をまたぐかまたがないか、もしくは格子点上に点がくるのかは、大きな違いになるので、グラフを書く際には注意が必要です。
反比例のグラフで気を付けたいところ
反比例のグラフではもう1点気を付けたいところがあります。
それはグラフの先の方です。
下のグラフに入れた赤丸の部分です。
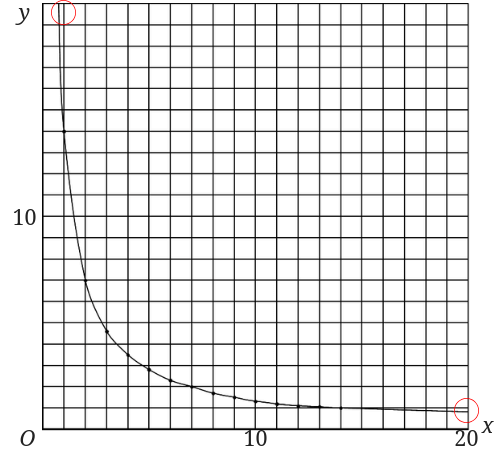 右側の赤丸の部分は、右に行けば行くほど\(x\)軸に段々近づいていきます。
右側の赤丸の部分は、右に行けば行くほど\(x\)軸に段々近づいていきます。
つまり右側に行けば行くほど\(x\)軸に近づくため、\(x\)軸から遠ざかるということはありません。
また、\(x\)軸には近づくだけで、\(x\)軸にくっついてしまうということもありません。
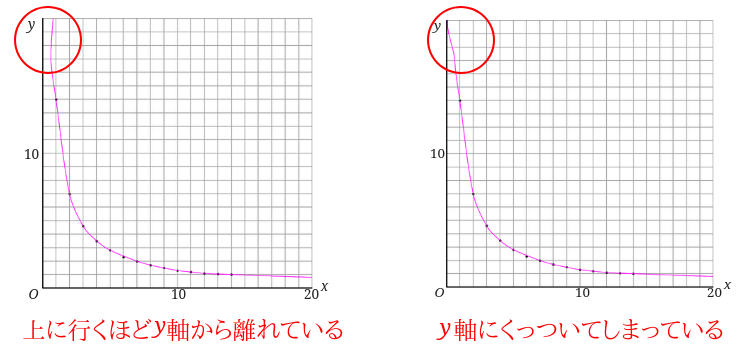
下のグラフのようになってはダメって事です。
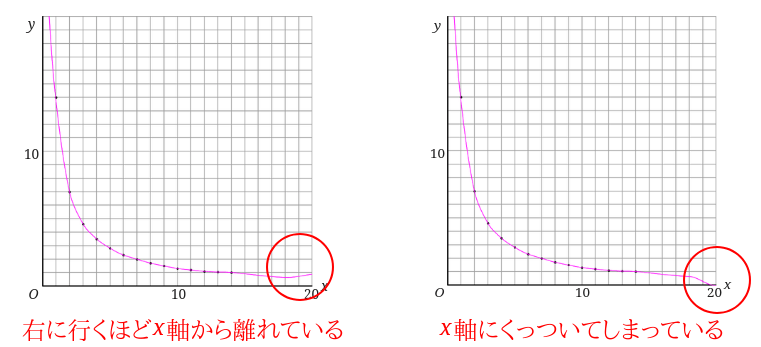
また左側の赤丸の部分は、上に行けば行くほど、\(y\)軸に近づいていきます。
先程の右側の赤丸の部分と同じように、上に行けば行くほど\(y\)軸に近づいていくため、\(y\)軸から遠ざかるということはありません。
また、\(y\)軸には近づくだけで、\(y\)軸にくっついてしまうということもありません。
下のグラフのようにならないようにしましょう。
まとめ
今回の記事では、反比例のグラフの書き方について書いてみました。
きちんと\(x\)に数をいれて、グラフが1つ1つどこを通るのかをはっきりさせておくことが大切です。
ある程度の数、点を打つと、誤差も少なくなります。
▼関連記事▼
・反比例の意味とは?比例と何が違うの?
References
| ↑1 | \(x\)座標も\(y\)座標も整数の点 |
|---|




