比例の次に登場する反比例。
反比例は中学1年生でも再び登場するので、きちんと小学生のうちに理解しておきたいところです。
今回の記事では反比例とは何か、反比例の意味について書いてみたいと思います。
反比例の意味と比例との違い
反比例とは何かということについて、例題を用いて見ていきましょう。
反比例しているのかについて考えてみましょう。
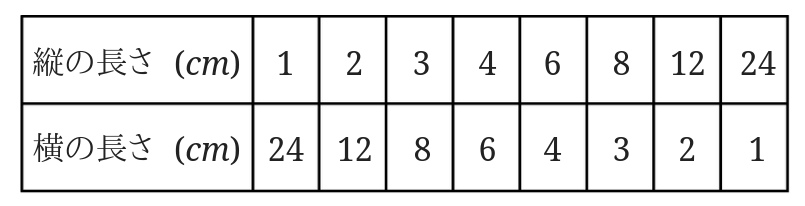
結論から言うと面積が\(24cm^2\)の長方形の縦の長さと横の長さは反比例の関係にあります。
それでは、なぜ反比例の関係にあると言えるのか、確認してみましょう。
まずは反比例とはどのような関係なのかについて押さえておきましょう。
反比例の意味とは
反比例とは、2つの量がある時に、片一方の量を2倍3倍…としたときに、もう一方の量が\(\frac{1}{2}\)倍\(\frac{1}{3}\)倍…となる2数の関係のことをいいます。
比例は、2つの量がある時に、片一方の量を2倍3倍…としたときに、もう一方の量も2倍3倍…となる2数の関係のことです。
そこを比較しておくと分かりやすいと思います。
また、これに加えて、反比例では2つの量を掛けると、いつも決まった数になるという性質があることを押さえておくとばっちりです。
反比例の意味が分かったら、先程の例題をみてみましょう。
比例の見分け方と同じように、\(x\)の値を2倍3倍…としたときの\(y\)の値から考えます。
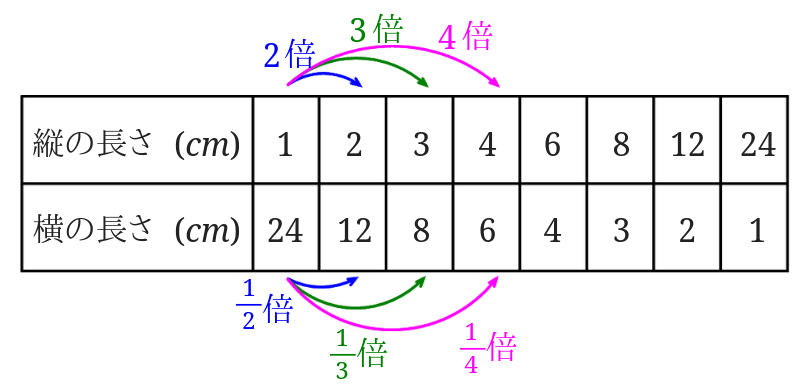
すると、縦の長さを2倍3倍…とすると、横の長さは\(\frac{1}{2}\)倍\(\frac{1}{3}\)倍…となっていることが分かります。
このことから、面積が\(24cm^2\)の長方形の縦の長さと横の長さは反比例の関係にあるといえます。
もっと簡単に反比例って判断できないの?
縦の長さの値を2倍3倍…としたときの横の長さの値がどのように変化するのかをみて判断するのはちょっと面倒です。
そんな時は、縦の長さと横の長さの値の積[1]縦の長さとと横の長さを掛けた数が一定であることを利用すると容易に求めることができます。
縦の長さと横の長さの積を書き出してみると、
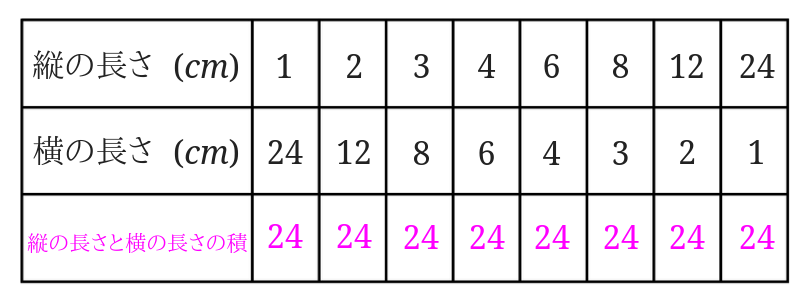
縦の長さと横の長さを掛けると全部\(24cm^2\)となりました。[2]長方形の面積が\(24cm^2\)になるように縦の長さと横の長さを設定したので、当然と言えば当然ですが…
このことから面積が\(24cm^2\)である長方形の縦の長さと横の長さは反比例の関係にあると言えます。
反比例では2つの量を掛けると、いつも決まった数になるのはなぜ?
反比例の一般式は、$$y=\frac{決まった数}{x}$$または$$y=決まった数\div x$$となります。[3]小学校の教科書では後者の$$y=決まった数\div x$$で載っていると思います。
後者の$$y=決まった数\div x$$を使って考えてみます。
ちょっとこのままでは見にくいので、$$決まった数\div x=y$$と式の形を変えてみました。
次に割り算の確かめ算を使います。[4]逆算ができるお子さんであれば単なる逆算と捉えてもOKです。
割り算の確かめ算とは、割り算の検算のことです。
例えば\(8\div 2=4\)となったときに、4が商として正しいのかを判断する仕方です。
この場合、\(2\times 4\)をして8になり、割られる数の8と等しくなったので、答えが合っていると判断する確かめ方です。
割り算では商と割る数を掛けると、割られる数になるという性質を使います。
$$決まった数\div x=y$$を確かめをしてみると、$$x\times y=決まった数$$となります。
このことから、反比例の関係にある2つの数を掛けると決まった数になることが分かります。
▼関連記事▼
・比例が分からない?反比例って何?を解決しよう!
まとめ
今回の記事では反比例とは何か、反比例の意味について書いてみました。
反比例の性質について覚えておきたいのは2点です。
・2つの量がある時に、片一方の量を2倍3倍…としたときに、もう一方の量が\(\frac{1}{2}\)倍\(\frac{1}{3}\)倍…となる
・2つの量を掛けると、いつも決まった数になる
特に1点目の「2つの量がある時に、片一方の量を2倍3倍…としたときに、もう一方の量が\(\frac{1}{2}\)倍\(\frac{1}{3}\)倍…となる」は、反比例が何かを理解するのにとても大切です。
必ず覚えておいてもらいましょう。
2点目は反比例かどうかの見分けるときに使うというよりも、グラフや表から、2つの量の関係式を求める時に大活躍してくれますよ。




