小学生のうちに知っておきたい比例の性質

比例の性質が分かると、表を求めることができたり、グラフを簡単に書けるようになったりいいことがたくさんです。

さらに比例は今後難しくなる算数や数学の基礎になります。

小学6年性で習う比例の性質について書いてみたいと思います。

 比例の性質ってなに？

例題を使って比例の性質をみて行きたいと思います。

順番にみていきましょう。
(1)\(x\)と\(y\)はどのような関係にありますか。
(2)\(x\)が2倍、3倍…となると、\(y\)はどのように変化しますか。
まずは表をみてみましょう。
りんごの個数が2倍、3倍…となると、りんごの値段も2倍、3倍…になっていますよね。

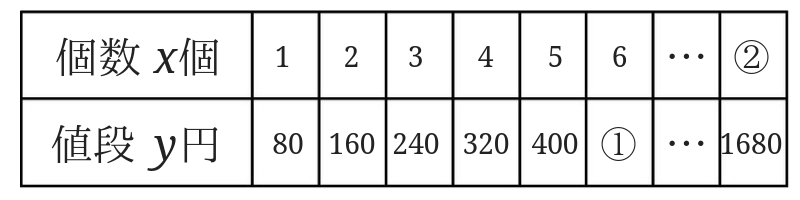
このように一方の量(数)を2倍3倍…としたときにもう一方の量(数)も2倍3倍…となっている2数の関係を比例の関係といいます。
(1)の答えは、「比例の関係」、(2)の答えは「2倍、3倍…になる。」、となります。

まずはしっかりと比例の関係を押さえるようにしましょう。
比例の関係とは「一方の量(数)を2倍3倍…としたときにもう一方の量(数)も2倍3倍…となっているような関係」とイメージできるといいと思います。
この見方をちょっと変えたのが(3)です。

(3)\(x\)が\(\frac{1}{2}\)倍、\(\frac{1}{3}\)倍…となると、\(y\)はどのように変化しますか。
先ほどは、「\(x\)が2倍、3倍…となったとき」となっていましたが、今度は「\(x\)が\(\frac{1}{2}\)倍、\(\frac{1}{3}\)倍…となったとき」の\(y\)の値の変化がどのようになるかという問題です。
実際に表で見てみると、

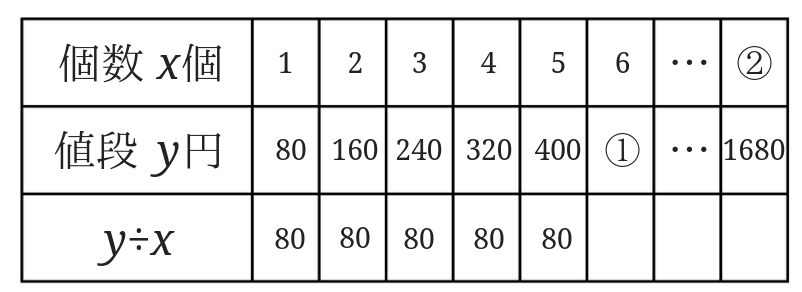
\(y\)も\(\frac{1}{2}\)倍、\(\frac{1}{3}\)倍…となっていることが分かります。
(3)の答えは「\(\frac{1}{2}\)倍、\(\frac{1}{3}\)倍…になる。」ということになります。
比例の関係とは、(2)から「一方の量(数)を2倍3倍…としたときにもう一方の量(数)も2倍3倍…となっているような関係」、(3)から「一方の量(数)を\(\frac{1}{2}\)倍\(\frac{1}{3}\)倍…としたときにもう一方の量(数)も\(\frac{1}{2}\)倍\(\frac{1}{3}\)倍…となっているような関係」ということが押さえることができていればばっちりです。

(4)\(x\)が1増えると、\(y\)はいくら増えますか。
\(x\)が1増えるということがどういうことなのかが分かればすんなり答えることができます。
\(x\)が1増えるというのは、りんごが1つ増えるということを意味します。
また\(x\)が1増えると、\(y\)はいくら増えるのかというのは、りんごの個数が1増えるとりんごの値段がいくら増えるのかということです。
つまり、りんごの個数が1個ふえるごとに、値段がいくら増えるのかを答えればいいということになります。
これは、80円ということになりますよね。

この問題では、\(x\)が1増えると、\(y\)はいくら増えるのか、つまり、\(y=\)決まった数\(\times x\)の決まった数はいくらなのかを答えればいいということになります。
このことが理解できるとやりやすいと思います。
この「決まった数」は、中学では比例定数^[1]一次関数では、傾きや変化の割合と呼ばれます。と呼ばれるようになります。

(5)\(y\)を\(x\)で割った商は何を表していますか。
\(y\)を\(x\)で割った商と言われるとなんだかイメージがしづらいなぁと感じるお子さんが多いと思います。
大抵のお子さんにとって何を表すのかなんて問題は面倒で分かりにくいものです。
まずは具体的なイメージをさせてあげられると分かりやすいのではないでしょうか。
この問いの場合であれば、\(y\)を\(x\)で割った商とイメージするのではなく、りんごの値段をりんごの個数で割った時の商は何を意味するのかを考えると分かりやすくなります。

例えば、りんご3個の値段は240円のとき、りんごの値段をりんごの個数で割ってみると\(240\div 3=80\)となります。
この80がりんご1個の値段を意味するのは、分かりやすいと思います。
このことから(4)の答えは、りんご1個の値段ということになります。

それでは問題文と同じように、\(y\)を\(x\)で割った商として考えます。
\(x\)が3のとき\(y\)は240です。
\(y\)を\(x\)で割ってみると、\(240\div 3=80\)となります。
この80が何を意味するのかというのは、この80とにらめっこしても、\(240\div 3\)をよく見ても分かりにくいものです。
きちんと意味を分かった上で、\(y\)を\(x\)で割った商を考えると解きやすいのではないでしょうか。

(6)①、②にあてはまる数を求めましょう。
①はりんごが6個のときの値段が分かればいいということです。
また、りんごの値段はりんごが1個増えるごとに80円増えます。

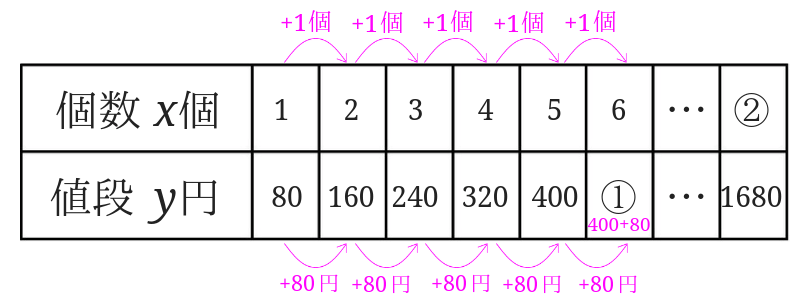
りんごが5個のとき400円なので、400円に80円を足して①の答えは480円と言うことになります。

もちろん、2つの数が比例の関係にあるのが分かっているので、比例の関係を利用して①を求めることもできます。
比例の関係では、「一方の量(数)を2倍3倍…としたときにもう一方の量(数)も2倍3倍…となっているような関係」です。
このことから、一方の量(数)を6倍するともう一方の量(数)も6倍となることが分かります。

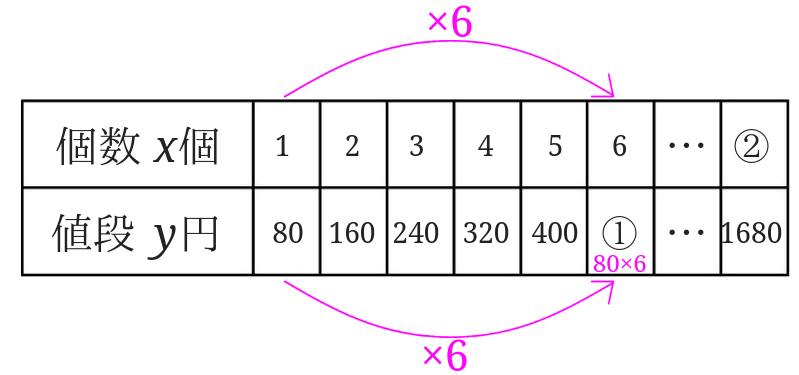
説明するときは、2倍、3倍、4倍、5倍、6倍と順番に見せてあげると分かりやすいです。

次に②の値を求めてみましょう。
②はりんごの値段が1680円になるときのりんごの個数を求めればいいということになります。
つまり、\(1680\div 80=21\)となるので、りんごの値段が1680円になるときのりんごの個数は21個ということが分かります。

まとめ

小学6年性で習う比例の性質について書いてみました。
比例の関係は、「一方の量(数)を2倍3倍…としたときにもう一方の量(数)も2倍3倍…となっているような関係」ということをきちんとお子さんに理解してもらっておきましょう。
ここの理解があると比例の理解は格段に上がります。

またお子さんが比例をうまく理解できないときは、問題文の題材を理解させることが大切です。
今回の問題だと、りんごの個数を\(x\)個りんごの値段を\(y\)円としました。
ただお子さんが分からない…と悩んでいるときに多いのは、このりんごの個数とりんごの値段の関係という意味がなくなっていることがよくあります。
りんごの個数とりんごの値段の関係という意味がなくなってしまうと、単なる\(x\)と\(y\)の関係としてみてしまいます。
そうなると、2数の関係をイメージしにくくなり、比例が分からないとなる子もいるので、具体的なものをイメージして学習していくことがおススメです。

最後に比例の性質をまとめておくと、
・一方の量(数)を2倍3倍…としたときにもう一方の量(数)も2倍3倍…となる
（一方の量(数)を\(\frac{1}{2}\)倍\(\frac{1}{3}\)倍…としたときにもう一方の量(数)も\(\frac{1}{2}\)倍\(\frac{1}{3}\)倍…となる）
・比例の式は、\(y=\)決まった数\(\times x\)

これに加えてこの記事では扱いませんでしたが
・グラフを必ず原点を通る直線になる
ということも是非押さえておきましょう。
▼関連記事▼
・小学生で習う算数の比例の意味