比例の単元では、式からグラフを書く場合と、逆にグラフから式を求める場合があります。
今回の記事では、グラフからxとyの関係を式に表す方法について書いてみたいと思います。
小学生の比例でグラフから式を求める問題を解いてみると…
例題を使って考えてみましょう。
\(x\)と\(y\)の関係を式にしましょう。
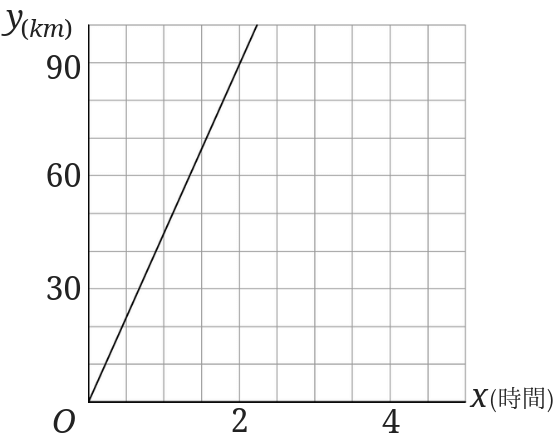
比例のグラフを、式にする問題です。
やり方はいくつかあると思いますが、まずは時速を求めて式を立てるやり方からみていきます。
時速を求めて式を立てる
実際は直接グラフから式を求めるというやり方ではなく、一旦時速を求めさせて、その次に\(x\)と\(y\)の関係を式に表させるという問題構成になっていることが多いです。[1]教科書ではあまり直接\(y=ax\)の形で尋ねられることは少ないかもしれせん。
この問いの場合だと、小問で
(1)この自動車の速さは、時速何\(km\)ですか。
(2)\(x\)と\(y\)の関係を式に表しましょう。
という感じです。
この流れに沿えば、(1)では、\( (2,90)\)の点から、時速45\(km\)をだします。
それから(2)の\(x\)と\(y\)の関係式は(1)で求めた時速45\(km\)を使って、\(y=45x\)が答えとなります。
答えは出せるのですが、なぜ\(y=45x\)となるのかが分かりにくいというお子さんは結構います。
なぜ、\(y=45x\)が答えとなるのでしょうか。
比例を理解するには決まった数の意味がポイント?!
教科書的には、\(y=\)決まった数\(\times x\)となっていると思います。
この決まった数が何を表しているのかが、分かればきちんと解けるということになります。
この決まった数は、中学になると、比例定数という名前に変わります。[2]一次関数では、変化の割合や傾きと呼ばれます。
この数は何を意味しているのかというと、「\(x\)が1増えたときの\(y\)の増加量」を表しています。
つまり、「決まった数」とは\(x\)が1増えたときに\(y\)がいくら増えるのかを示す数と分かります。
先程は時速\(45km\)と(1)で求めて、(2)では\(y=45x\)としました。
こうなる理由は、「決まった数」=「\(x\)が1増えたときの\(y\)の増加量」という点から考えると分かりやすいです。
「\(x\)が1増えたときの\(y\)の増加量」と言うのは、この問いの中では1時間で何\(km\)進むのかということを意味しています。
つまり、小問の1で時速を求めさせるのは、速さを求めさせる目的ではなく、決まった数を求めることを目的としています。
時速が分かればグラフの式が分かると言うことになります。
1時間ごとに進む道のりが時速そのものだということが分かれば、\(y=45x\)と自信をもって書くことができます。
ここまで理解するのは大変かもしれませんが、中学など進学した後で活きてくると思います。
この辺りの理屈がきちんと理解できていれば、誘導なしでも解けるようになります。
中学になると直接\(x\)と\(y\)の関係の式を求めることが多いので、誘導なしでも\(x\)と\(y\)の関係式を求められると後々有利になると思います。
グラフから決まった数を求めて答えを出す方法
\(y=\)決まった数\(\times x\)の決まった数というのは、「\(x\)が1増えたときの\(y\)の増加量」を意味していると先程書きました。
このことを利用して、決まった数を求めてみましょう。
決まった数は「\(x\)が1増えたときの\(y\)の増加量」ということから、
決まった数=\(y\)の増加量÷\(x\)の増加量[3]$$変化の割合=\frac{yの増加量}{xの増加量}$$と中学校で習います。
という事が分かります。
比例の場合は原点を必ず通るので、もう1点\(x\)座標も\(y\)座標も整数の点[4]格子点といいます。を探します。
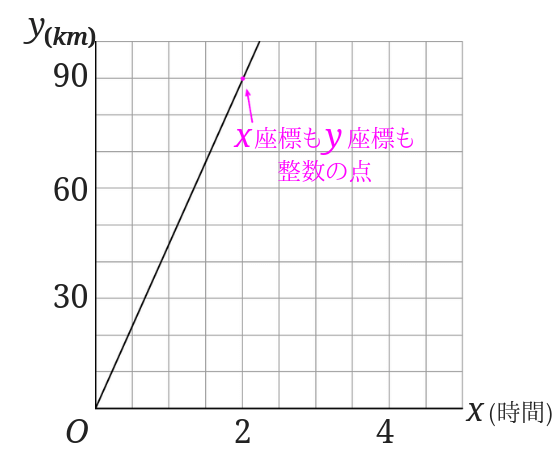
次に原点からその格子点にいくまでの\(x\)の増加量と\(y\)の増加量を求めます。
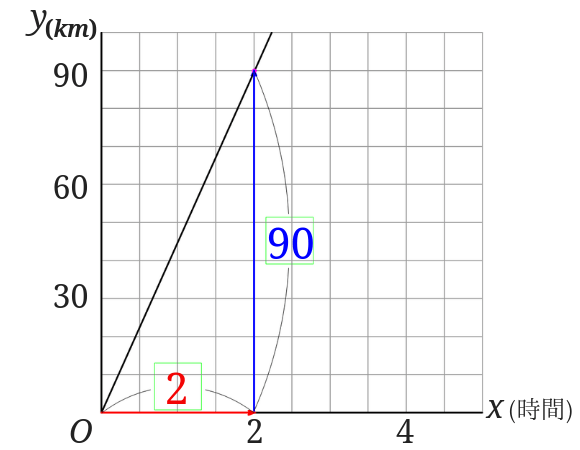
\(x\)の増加量と\(y\)の増加量が分かれば、決まった数を求めることができます。
この場合だと
決まった数は\(90\div 2=45\)となり45が決まった数という事が分かります。
決まった数が分かればあとは、
\(y=\)決まった数\(\times x\)に当てはめて、答えは\(y=45x\)となります。
まとめ
今回の記事では、グラフから\(x\)と\(y\)の関係を式に表す方法について書いてみました。
比例は、今後の数学の基礎になります。
ここが分からなければ、中学以降の数学でピンチになる可能性が非常に高くなります。
ただ答えが出せるというだけでなく、理屈などがきちんと分かるようにしておくと今後が優位になります。
特に、決まった数が、「\(x\)が1増えたときの\(y\)の増加量」を表しているということは是非理解、覚えさせておきたいことです。
▼関連記事▼
比例の意味が分からないときはこちら




