速さが途中で変わる文章問題の解き方

基本的な速さの計算ができるになったら次は文章題です。
大抵のお子さんにとってはこの辺りからがさらに難関となります。
応用問題に入ってから速さが嫌になる子も多いです。

速さの文章題はとても苦手とする子が多いところになります。
速さの文章題がきっちり解けることは中学校でも生きてきます。
というよりも中学1年生の速さの文章題って小学校の内容とかなり近いところがあります。
一応方程式を使うという建前があるので解き方は少し違いますが、解き方にこだわらなければ小学生でも中学1年生で扱う速さの問題は十分に解くことができるものです。
中学1年生で扱う速さの問題は小学校6年生の時にどれだけ理解して解けているかが問われるところにもなります。

しっかり理解して解けるようになっておくと、中学に入ってからいいことがありますよ。

速さが途中で変わる文章問題の解き方

基本的な速さの問題は解けるようになりましたか？
単純な問題は余裕で解けるようにしておくといいですよ。

それでは早速例題から見ていきましょう。

例題

家から学校まで行くのに途中まで分速$70m$ の速さで10分歩き、その後分速$130m$の速さで2分走りました
家から学校までの距離は何$m$ありますか。

きちんと読むとそんなにややこしい訳ではないのですが、なんとなく「文章題＝難しい」と思ってしまっているお子さんは多いです。
まずは問題文を絵や図を用いて書くと理解しやすくなります。
問題文中にあることをそのまま書きます。
例えばこの問題であればスタート地点が家なので、まずは家を描きます。
家なんてどうでもよさそうなものですが、問題文をイメージできることが大切です。

次に駅まで行くので駅を描いて…と絵や図を書いて解いていく感じです。
解き方が幼いと感じてしまう方もいると思いますが、文章題をイメージするにはもってこいです。
もちろんそんなにこった絵にする必要はなく、問題がイメージで切ればOKです。
本当に簡単なもので大丈夫です。
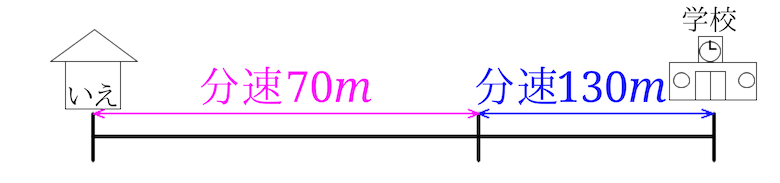それでは説明していきますね。
家から駅まで行く途中のあるところまで分速$70m$で10分、その後分速$130m$で2分進んで駅まで着いたので「家から途中地点までの距離」と「途中地点から駅までの距離」を足せば答えが求められます。$$70m\times 10+130m\times 2=700+260=960$$とな

るので、家から駅までの距離は$960m$ということが分かりました。
まずは情報を整理するのが大切ですよ。

例題

家から駅まで$1600m$の距離があります。
分速$300m$で3分自転車に乗って進んだ後分速$200$で何分進むと駅に着きますか。

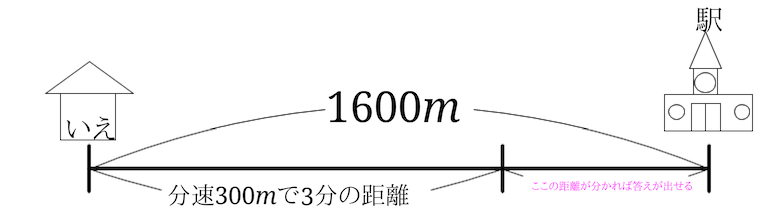
少しずつ情報が増えて来たので難しくなってきました。
分速$200m$で進んだ時間を求めたいので、分速$200m$で進んだ距離を求められれば解けそうです。
まずは分速$300m$で3分進んだ距離を求めます。$$300m\times 3=900$$分速$300m$で3分進んだ距離は$900m$ということが分かりました。
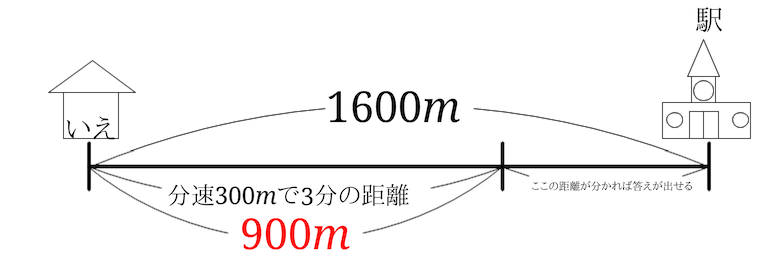分速$170m$で進んだ距離は、全体$1600m$から分速$300m$で進んだ距離$900m$の差ということになります。

分速$170m$で進んだ距離は、$$1600-900=700$$となり、$700m$だということが分かります。
分速$200m$で、$700m$進んだ時間を求めればいいので、$$700\div200=3.5$$となるので、求める答えは3.5分となります。

なんだか難しい感じでしたが、きちんと順を追って解いていくと新しい知識は1つも使わずに解くことができました。

練習問題

1、太郎くんが自分の家から花子さんの家まで歩いて行きます。
太郎くんが分速$60m$で10分歩きその後分速$75m$の速さで6分歩いて花子さんの家に着いた時、太郎くんの家から花子さんの家までは何$m$ありますか。

2、家から隣町の公園までサイクリングします。
時速$10km$の速さで0.5時間自転車に乗った後分速$200m$の速さで5分乗ると公園に着きました。
家から隣町の公園までの距離は何$m$ですか。

3、駅から家までの距離は$4740m$あります。
駅から時速$54km$のバスに5分乗ったと分速$60m$の速さで歩いた時、バスを降りてから家に着くまで何分かかりますか。

4、A駅から博物館まで電車とバスで移動します。
A駅からB駅までは電車で、B駅から博物館まではバスで移動します。
A駅から博物館までの距離は$75km$です。
ただし待ち時間は考えないものとします。
①A駅からB駅まで時速$140km$の電車で15分移動しました。
A駅からB駅までの距離は何$km$ですか。

②B駅から博物館までの距離は何$km$ですか。

③時速$60km$のバスに乗ってB駅から博物館まで行きました。
バスに乗った時間は何分になりますか。

解答と解説

1の解説

最初の例題と同じ形ですね。
分速$60m$で進んだ距離と、分速$75m$で進んだ距離を足すと答えが出せそうです。$$60m\times 10+75m\times 6=1050$$となるので、求める答えは$1050m$となります。

2の解説

1と解き方は基本的には同じです。
時速$10km$で進んだ距離と分速$200m$で進んだ距離を足せば答えは出せそうです。$$10km\times 0.5+200m\times 5=1005$$と、してしまうと間違いです。
ここで速さの2つの単位をよく見ると距離の単位が違います。
答えが$m$で答えるようになっているので、時速$10km$を$m$に合わせると、時速$10000m$となります。
あとは計算をして、$$10000m\times 0.5+200m\times 5=6000m$$となるので、求める答えは$6000m$となります。

3の解説

2つ目の例題と似た問題です。
この問題も先ほどの問題と同じで単位が揃っていないので単位を合わせることから始めます。
時速$54km$を$m$に、さらに分速にすると、分速$900m$となります。
時速$54km$で進んだ距離は$$900m\times 5=4500m$$
分速$60m$で歩いた距離は、全体の距離と時速$54km$で進んだ距離の差なので、$$4740-4500=240$$
分速$60m$で$240m$進んだので、$$240\div 60=4$$となるので、求める答えは4分となります。

4の解説

15分は$\frac{15}{60}$です。
時速$140km$で$\frac{15}{60}$分移動したので、$$140km\times \frac{15}{60}=35$$となるので、求める答えは$35km$となります。

②B駅から博物館までの距離は何$km$ですか。
A駅から博物館までの距離は$72km$。
①でA駅からB駅までの距離は$35km$と求めたので、$$75-35=40$$となるので、求める答えは$40km$となります。

③時速$60km$のバスに乗ってB駅から博物館まで行きました。
バスに乗った時間は何分になりますか。
時速$60km$で$40km$進んだので、$$40\div 60=\frac{40}{60}$$となるので、$\frac{40}{60}$時間となります。
問題では時間の単位は分で答えるようになっているので、時間の単位を時間から分に変えて、$$60\times \frac{40}{60}=40$$となり、求める答えは40分となります。