速さの三公式の中でも唯一掛け算で処理ができる道のりは比較的理解がしやすいものです。
時速10キロメートルで進む車が2時間進んだ距離を求める事はそんなに難しくありません。
10×2としてしまえば答えはすぐに出てきてしまいます。
しかし、おなじ道のりを求める公式でも、難しいのが速さの単位と時間の単位が揃っていない場合の問題です。
時速が与えられているのに与えられた時間の単位が分という問題の場合は、急に問題の難易度が上がってしまいます。
実際にはそんなに難易度は上がっていないのですが、公式を「道のり(距離)=速さ×時間」と丸暗記しているお子さんは単位を気にせず計算してしまい間違ってしまうことが多くなります。
これは何故かと言うと、速さや時間という言葉に振り回されてしまい、それぞれの単位にまで意識がいかないからです。
ただ公式に数字を入れればいいと言えばそうなのですが、「単位を揃えて」というのを忘れがちです。
少し意味を考えればそんなに難しいものではありません。
速さの表し方をしっかり理解していればそんなに難しくないのに、公式に入れるだけと考えていると難しくなる…
楽に解くために覚えた公式が仇となってしまうんですね。
不思議です。
今回の記事では速さと時間の単位が揃っていない道のりの出し方をやっていきます。
やることそのものはそんなに難しくありませんので1つ1つ整理しながら見ていきましょう。
速さと時間の単位が揃っていない道のりの求め方
お子さんが算数の問題でちょっと難しくなるとすぐにできなくなるという場合は根本的なところの理解ができていないことが多いです。
速さの単元では基本的な問題であれば公式に数字を入れれば答えが簡単に出てきます。
しかし、単純に丸暗記をしていると少し単位が揃っていなかったり、問題がややこしくなったりするだけで突然問題が解けなくなってしまいます。
そんなことにならないようにするためにまずは基本をしっかり押さえましょう。
この速さの単元では、その表し方が基本になります。
秒速・分速・時速。
この3つの言葉の意味をしっかり押さえることが速さの問題を楽に解けるようになるコツになります。
お子さんが少し用語に対して理解が怪しいなんていう場合はこちらの記事を先に読んで見てください。
・秒速、分速、時速といった速さの単位の意味とは
それでは早速例題をもとに解き方を見ていきましょう。
この自動車が2分間に進む距離は何\(km\)でしょうか。
道のり(距離)を求める公式「道のり(距離)=速さ×時間」を使って解くと、\(60\times2=120\)となります。
結果答えは\(120km\)ということになります。
ちょっとここで考えてみましょう。
2分間をまずイメージしてくださいね。
その2分間の間に\(120km\)進む自動車…
とんでもないスピードですよね。
時速\(3600km\)…笑
現実的にありませんよね。
でも結構書いちゃう子がいるんですよね。
算数や数学ではあんまり現実離れした数字が出ることはありません。
ちょっとおかしいよね!って気づけるくらいの余裕があるといいですね。
時速を分速に変えて計算する方法
さて問題に戻りますね。
丁寧に解いていきますよ。
まず考えるのは速さです。
時速\(60km\)は1時間に\(60km\)進むという意味です。
2分間に進む距離を求めたいのですが、今わかっているのは1時間に進む距離だけです。
1分間に進む距離…分速が分かれば、答えが求めやすそうです。
分速は\(60km\div 60=1\)となるので分速\(1km\)になります。
1分間に進む距離が\(1km\)ということが分かったので、2分間に進む距離は、$$1km\times2=2km$$で求められます。
答えは\(2km\)ということになります。
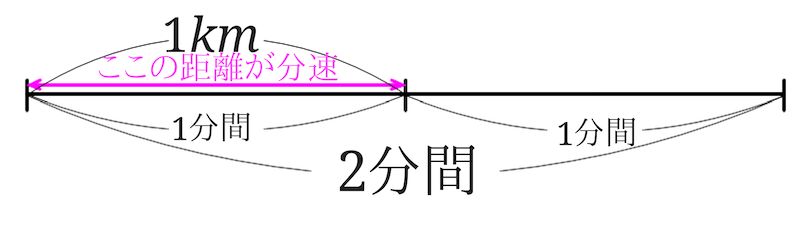 この時方では、時速を分速に変えて答えを求めました。
この時方では、時速を分速に変えて答えを求めました。
今度は時間の単位を変えて計算する方法をやってみます。
時間の単位を〇分から△時間に変えて計算する方法
問題文で1時間あたりに進む距離が分かっているので、2分を△時間に変えてから答えを求めてみます。
時間の単位を分から時間に変えるには、2分を\(60\)で割ることで、△時間に変えることができます。[1] … Continue reading
\(2\div 60=\frac{2}{60}\)となるので時間は\(\frac{2}{60}\)時間となります。
1時間に\(60km\)進むので、\(\frac{2}{60}\)時間で進む距離は、$$60km\times \frac{2}{60}=2km$$となります。
答えは\(2km\)ということになります。
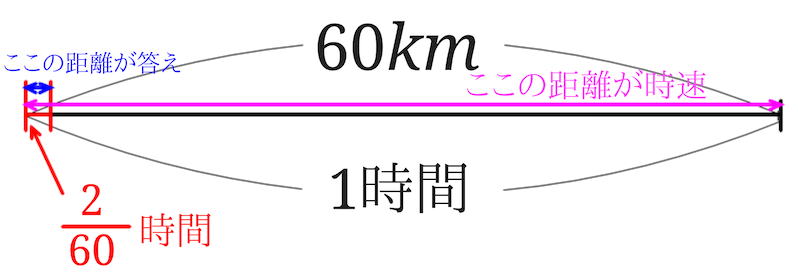 意味を考えればそんなにややこしい計算や考え方はでてきませんね。
意味を考えればそんなにややこしい計算や考え方はでてきませんね。
しかし、慣れるまでは難しいと思います。
何度も同じように考えられるといいですね。
練習問題
1、時速\(120km\)で走る電車で40分移動すると何\(km\)移動したことになりますか。
2、分速\(300m\)の自転車で家から0.75時間かかる公園は家から何\(m\)の距離にありますか。
3、秒速\(5m\)で\(\frac{3}{2}\)分走ると何\(m\)走ったことになりますか。
4、家から時速\(15km\)の自転車に乗ると300秒で公園に着きました。
家から公園までの距離は何\(km\)ですか。
5、秒速\(\frac{3}{10}cm\)で動くカメが0.5時間動いたとき、その距離は何\(cm\)になりますか。
解答や解説
1の解説
時速を分速に変えて計算する方法
時速\(120km\)は60分で\(120km\)進むということなので、$$120km\div 60=2$$となるので、分速\(2km\)ということになります。
1分間に\(2km\)で40分進むので、$$2km\times 40=80km$$となるので\(80km\)移動したことになります。
時間の単位を分から時間に変えて計算する方法
40分を時間に変えると$$40\div 60=\frac{40}{60}$$となります。
よって移動した時間は\(\frac{40}{60}\)時間ということになります。
1時間に\(120km\)進むので、$$120km\times \frac{40}{60}=80$$となるので、答えは\(80km\)ということになります。
計算途中で\(\frac{40}{60}\)が約分できるけれど、時速\(120km\)と掛け合わせることが分かっているのでここではしませんでした。
あとで120と60を約分で消すことで楽に計算ができます。
ちょっとしたことですが、お子さんに余裕がある時はその辺りまで教えてあげてもいいかもしれませんね。
もちろん\(\frac{2}{3}\)と約分をあらかじめ計算してもOKですよ。
2の解説
分速を時速に変えて計算する方法
1分間\(300m\)進むので60分で進む距離は、$$300m\times 60=18000m$$となり、時速\(18000m\)となります。
1時間に\(18000m\)進むので、$$18000m\times 0.75=13500$$となり、答えは\(13500m\)となります。
時間の単位を時間から分に変えて解く方法
時間が小数になるとイメージしづらくなるので分数で考えるのがおススメです。
0.75時間は\(\frac{3}{4}\)時間になります。
時計をイメージしてみてくださいね。
\(\frac{3}{4}\)ということは…はい!45分ですね。
ピンと来ないときは60分の\(\frac{3}{4}\)なので、$$60\times \frac{3}{4}=45$$となり、0.75時間は45分ということになります。
もちろん小数のままでもいいのですが、分数のほうがイメージしやすいと思いますよ。
1分間に\(300m\)で45分進むので、$$300m\times 45=13500$$となるので、答えは\(13500m\)となります。
3の解説
秒速を分速に変えて解く方法
1秒間に\(5m\)進むとき、60秒で進む距離は、$$5\times 60=300$$となり分速\(300m\)となります。
1分間に\(300m\)進むとき\(\frac{3}{2}\)分で進む距離は、$$300m\times \frac{3}{2}=450$$となるので、答えは\(450m\)となります。
時間の単位を分から秒に変えて解く方法
\(\frac{3}{2}\)分は90秒です。
1秒間に\(5m\)進むとき90秒で進む距離は、$$5m\times 90=450$$となるので、答えは\(450mとなります。\)
4の解説
時速を秒速に変えて解く方法
3600秒間に\(15km\)進むので、1秒間に進む距離は$$15\div 3600=\frac{15}{3600}$$となるので、秒速\(\frac{15}{3600}km\)となります。
300秒間に進む距離を求めるので$$\frac{15}{3600}km\times 300=\frac{5}{4}$$となり、答えは\(\frac{5}{4}km\)となります。
時間の単位を秒から時間に変えて解く方法
300秒は5分です。
5分を時間にすると\(\frac{5}{60}\)時間となります。[2] … Continue reading
1時間に\(15km\)進むので、$$15km\times \frac{5}{60}=\frac{5}{4}$$となるので、答えは\(\frac{5}{4}km\)となります。
5の解説
秒速を時速に変えて解く方法
1秒間に\(\frac{3}{10}cm\)進むので1時間に進む距離は、$$\frac{3}{10}cm\times 3600=1080$$となるので、時速\(1080cm\)ということになります。
1時間に\(1080m\)の速さで0.5時間進むので\(1080m\times 0.5=540\)となり、答えは\(540cm\)となります。
時間の単位を時間から秒に単位変換して解く方法
0.5時間は\(\frac{1}{2}\)時間です。
時計を眺めてみると、1時間の\(\frac{1}{2}\)は30分です。
1分は60秒なので、$$30分\times 60=1800$$となり、0.5時間は1800秒であることが分かります。
1秒間に\(\frac{3}{10}cm\)で1800秒進むときの距離は、$$\frac{3}{10}cm\times 1800=540$$となり、答えは\(540cm\)となります。
まとめ
今回の記事ではちょっと面倒な道のり(距離)を求める問題を扱いました。
単位をうまく変換できるかが問題を解けるかどうかの分かれ道となりそうですね。
今回のように単に計算するのにひと手間かかるような問題は、お子さんの理解度がどれほどあるのかを見るにはいい問題です。
基礎が大事とは言われますが、算数の場合は基本的過ぎて理解できているのかできていないのかが分からないこともあります。
うまくちょっと手間のかかる問題を使うことでお子さんの理解力を見ることができるのではないでしょうか。
References




