小学4年生でならう倍の計算は、割り算の単元に属します。
しかし、小学5年生の割合の単元の要素も持っているため、意外と難しく感じるお子さんもいます。
と、言うよりも実はきちんと学んでいくと難しい単元だと思います。
割り算で言うと等分除の考え方で考えると上手くできるようになります。
今回の記事では、倍の計算のもとにする量が分からない時の文章問題の教え方について書いてみたいと思います。
もとにする量が不明なときの倍の計算の文章問題の教え方
倍の計算の求め方です。
ここでは、あるものを「何倍かした数」と「何倍したのか」が分かっている問題を扱ってみたいと思います。
それでは早速例題を見ていきましょう。
長さがはっきりしていないと、絵図にしても線分図にしても描きにくいものです。
この場合は赤いリボンの長さと青いリボンの長さの比が、1:7ということが分かっています。
まずは青いリボンを描いてみましょう。

次に赤いリボンを描きます。
赤いリボンの長さは青いリボンの長さの7倍なので、青いリボンの長さ7つ分を赤いリボンの長さにしましょう。
7つ分となると定規などを使いたくなるかもしれませんが、目分量で大体7倍くらいが描けるようにしておくといいと思いますよ。

青いリボンは赤いリボンを7等分したときの赤いリボン1本の長さと等しいということですね。
\(49\div 7=7\)となるので、青いリボンの長さは\(7cm\)ということになります。
もう1問例題を解いてみましょう。
線分図で解いてみる
図としては線分図で解くのが解きやすいと思います。
まずは線分図を描いてみましょう。
花子さんは24枚のシールを持っています。

花子さんのシールの枚数はたろうくんのシールの枚数の4倍なので、線分図を4等分してみます。
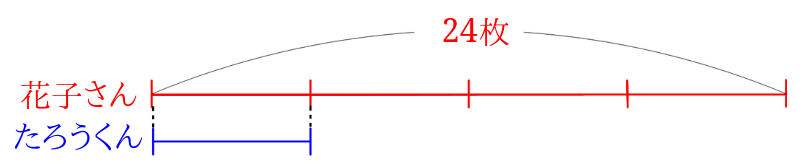
たろうくんのシールの枚数を4等分したときの1つ分が花子さんの持っているシールの枚数になります。
\(24\div 4=6\)となり、たろうくんの持っているシールの枚数は6枚ということが分かりました。
絵図で解いてみる
図としては線分図が描きやすい気がしますが、絵図でも簡単に解くことができます。
花子さんはたろうくんの4倍のシールを持っているので、花子さんのシールを4等分したときの1つ分がたろうくんのシールの枚数と言うことになります。
ここでちょっと見方を変えてみましょう。
4等分と考えるとやりにくいので、4人の人に同じ枚数ずつのシールを配ることを考えてみます。
このときイメージするといいのがトランプです。
4人でトランプを同じ枚数ずつ配るときって、カードを1枚ずつ配りますよね。
この要領で配っていくと4等分にできるというのはイメージがしやすいのではないでしょうか。
1枚ずつ配ってみました。
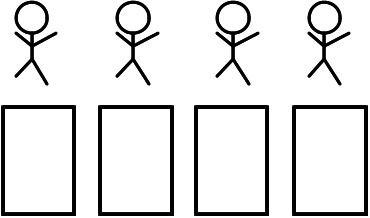
2枚ずつ配ってみました。
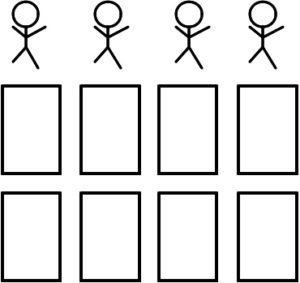
この要領で24枚すべてを配ってしまいましょう。
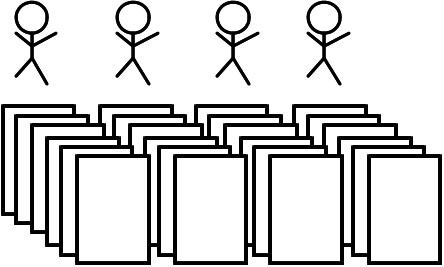
これで4等分できましたね。
たろうくんの持っているシールは6枚ということが分かります。
練習問題
1、えん筆の長さは、消しゴムの長さの3倍で、15\(cm\)あります。消しゴムの長さは何\(cm\)ですか。
2、親のくまの体重は81\(kg\)で、これは子ぐまの体重の9倍にあたります。子ぐまの体重は何\(kg\)ですか。
3、チョコレート1つのねだんはあめ玉1つのねだんの6倍で、42円です。あめ玉1つのねだんはいくらですか。
解答と解説
1の解説
絵図でも線分図でも描きやすい問題ですね。
えん筆から描いてみましょう。
そこに長さを書き込み、消しゴムを書き込んでみましょう。
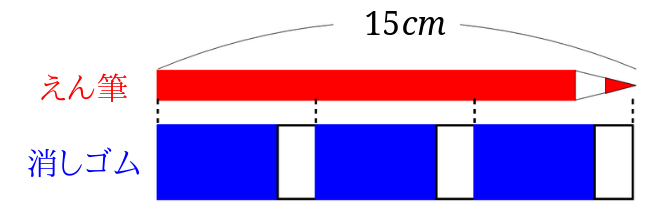
えん筆の長さを3等分すればいいので、\(15\div 3=5\)となり、消しゴムの長さは\(5cm\)になります。
2の解説
体重は目に見えないので線分図で解くのがやりやすいと思います。
まずは親のくまの体重を示す線分図を描きましょう。

次に親の体重は子ぐまの体重の9倍なので、線分図を9等分してみます。

9等分した1つ分の長さが、子ぐまの体重にあたるので、\(81\div 9=9\)となり、子ぐまの体重は\(9kg\)と言うことが分かりました。
3の解説
値段を扱う問題では線分図が使いやすいと思います。
まずはチョコレートの値段を示す線分図を描いてみましょう。

チョコレートの1つの値段はあめ玉1つの値段の6倍なので、6等分してみましょう。

6等分したものの1つ分があめ玉1つの値段になるので、\(42\div 6=7\)となり、あめ玉1つの値段は7円ということになります。
まとめ
今回の記事では、倍の計算のもとにする量が分からない時の文章問題の教え方について書いてみました。
割り算のイメージがつかめないと分かりにくいかもしれません。
なんとなく割り算だ!ということで、答えが合う子もいますが、できればきちんと割り算の意味を理解したうえで解きたいところです。
そのためにも面倒に感じてしまうかもしれませんが、絵図や線分図はおすすめの解き方でです。
絵図や線分図を使うと割り算のイメージもつかみやすくなると思いますよ。
【関連記事はこちら】
・倍の計算の教え方のコツは?割り算になるのはどうして?




