小学生にとって分数というだけでもその計算は難しいものです。
かけ算だと分子同士、分母同士を掛ければ答えが出せますが、分数の割り算となるとそれが急にうまくいかなくなります。
分数の割り算だと、分母と分子を入れ替えて掛けることで計算することができます。
それだけと言えばそれだけですが、これがなぜそうなるの?と考えると「うーん」となってしまうお子さんが大半なのではないでしょうか。
またお子さんが「どうして分数の割り算だと分母と分子を入れ替えて掛けるの?」という疑問を持ったとしても、計算するというだけでは「そういうものだから暗記しなさい」と言われちゃうお子さんもおられるのではないでしょうか。
今回の記事では、分数の割り算ではなぜ分母と分子を入れ替えた数を掛けると計算できるのかということについて書いてみたいと思います。
分数の割り算ってなぜ逆数を掛けるの?
分数の割り算ってなんとなく割る数の逆数を掛ければ計算できるとして片づけてしまうことが多いのではないでしょうか。
そうすればできるのは分かっても「なぜ逆数をかけるのか?」と考えると難しいものですよね。
一応大人に説明するにはそんなに難しくならないと思うのですが、これが小学生に説明するとなるとどう説明したらいいのかが難しくなってしまいます。
まずは、繁分数を使って「分数の割り算では割る数の逆数を掛けるのか」についえ考えてみたいと思います。
$$(1)\frac{2}{7}\div \frac{5}{3}$$
この例題を使って考えてみたいと思います。$$〇\div △=\frac{〇}{△}$$を使います。
例えば\(2\div 3=\frac{2}{3}\)という感じですね。
これを\(\frac{2}{7}\div \frac{5}{3}\)に当てはめてみると、〇は\(\frac{2}{7}\)、△は\(\frac{5}{3}\)ということになります。
\(〇\div △=\frac{〇}{△}\)の通りにしてみると、$$\frac{2}{7}\div \frac{5}{3}=\frac{\frac{2}{7}}{\frac{5}{3}}$$という感じになります。
次に分母の逆数を分母と分子にかけてみましょう。$$\frac{\frac{2}{7}\times \frac{3}{5}}{\frac{5}{3}\times \frac{3}{5}}$$となりました。
後は約分すると、
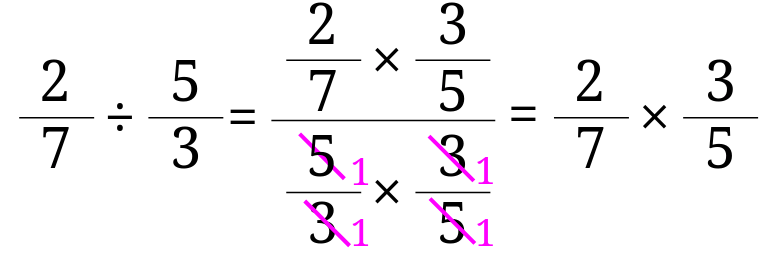
$$\frac{2}{7}\times \frac{3}{5}$$なんだか逆数を掛けた感じになりましたね。
これだと分数の割り算の計算では割る数の逆数を掛けるっぽい感じではありますが、本当に「分数の割り算の計算は逆数を掛ければいいのか」について「そうだ」とは言い切れません。
これを文字でやってみましょう。
\(a\div \frac{b}{c}\)をもとに考えてみます。
先ほどと同じように、式を変形していきましょう。
\(a\div \frac{b}{c}=\frac{a}{\frac{b}{c}} \)となります。
分子と分母に\(\frac{c}{b}\)を掛けてみると、\(\frac{a}{\frac{b}{c}}=\frac{a\times \frac{c}{b}}{\frac{b}{c}\times \frac{c}{b}}=a\times \frac{c}{b} \)となりました。
よって、分数の割り算の計算では逆数を掛けることで計算することができることが分かりました。
理屈としてはこのやり方で説明ができるのですが、問題なのが小学生のお子さんが理解できるのか?ということです。
分数の割り算はなぜひっくり返すのかということを小学生にもわかるように説明するにはどうすればいいのでしょうか。
分数の割り算はなぜひっくり返すのか
先ほどの\(a\div \frac{b}{c}\)を使って考えてみましょう。
まずは\(a\div b\)は、\(\frac{a}{b}\)ということはすんなりできるのではないでしょうか。
\(a\div b=\frac{a}{b}\)の\(\frac{a}{b}\)が意味するのは、どんなことなのか考えてみると、「\(a\)の中に\(b\)が入っている数(包含除)」もしくは「\(a\)を\(b\)等分したときの1つ分(等分除)」と言うことになります。
「\(a\)の中に\(b\)が入っている数(包含除)」を使って分数の割り算はなぜ割る数をひっくり返して掛けるのかということについて紐解いていきたいと思います。
次に\(a\div \frac{b}{c}\)を考えてみます。
\(a\div b=\frac{a}{b}\)は、\(a\)の中に\(b\)がいくつ入っているのかということを表していました。
また同じように\(a\div \frac{b}{c}\)を考えると、この式の答えは、\(a\)の中に\(\frac{b}{c}\)が入る個数となります。
\(b\)の中には\(\frac{b}{c}\)が\(c\)個入ります。
\(a\div \frac{b}{c}\)の答えは\(a\div b\)の答えの\(c\)倍ということになります。
よって、\(a\div \frac{b}{c}\)の答えは\(a\div b\)の答えのを\(c\)倍して、\(\frac{a}{b}\times c=a\times \frac{c}{b}\)となり、分数の割り算では割る数の逆数を掛けることで計算できることが分かりました。
まとめ
今回の記事では、今回の記事では、分数の割り算ではなぜ分母と分子を入れ替えた数を掛けると計算できるのかということについて書いてみました。
分数の割り算では割る数の逆数を掛けることで計算できることをきちんと理解するのは、結構難しいです。
どうしても理屈がややこしくなってしまいます。
いっそのこと、繁分数を小学生に教えてしまったほうが、理屈的には納得してもらいやすい気がします。
小学生に繁分数は難しそうに見えますが、無理難題という感じにはなりません。
後々を考えても繁分数を教えちゃうのも手かもしれませんね。




