何倍かが分かっている、倍の計算の単元をみていきましょう。
今回の記事では何倍かが分かっているときの倍の計算の教え方のコツについて書てみたいと思います。
割り算の単元なのにかけ算を使う「倍の計算」って？
割り算の単元なのですが、ここでは掛け算を使います。
単元から使うべき計算方法を考えてしまうお子さんにはちょっとやりにくいところかもしれません。
しかし、きちんと意味を考えて解いてみると、解きやすいところです。
1つずつ意味を考えながら理解していきましょう。
それでは例題を見ていきましょう。
まずは文章問題がどんなことを言っているのかを理解するために絵図を描いてみましょう。
青い色紙が3まいあるということなので、青い色紙を3まい描いてみましょう。
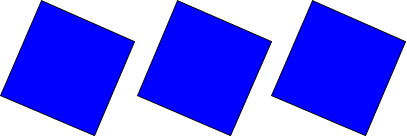
赤い色紙は青い色紙の4倍の枚数があるので、赤い色紙は3枚のかたまりが4つあるということになります。
赤い色紙は3枚のかたまりが4つあるので、\(3\times 4=12\)となります。
このことから赤い色紙の枚数は12まいとなります。
それではもう1つ例題を見てみましょう。
呼んだページ数は絵図にしにくいので、線分図で考えてみます。
たろうくんが読んだページを線分図で描いてみます。
線分図の長さは適度なところで大丈夫です。
あまり長くしてしまうと、解きにくくなるのでそれなりな大きさで描きましょう。
花子さんはたろうくんのよんだページの6倍読んだので、たろうくんの読んだページを表した線分図を6つ繋げてみます。
方眼の用紙であれば方眼を頼りに、白紙の場合は定規を使って書くと分かりやすくなります。
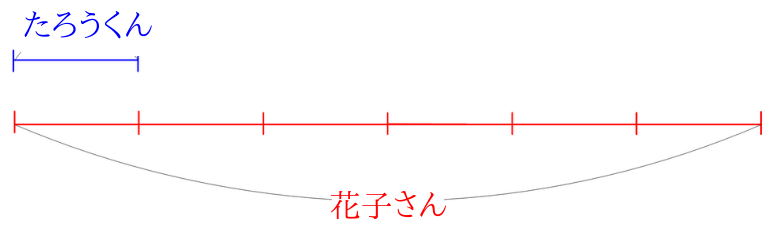花子さんの読んだページはたろうくんの読んだページ数の6倍なので、\(5\times 6=30\)となります。
花子さんの読んだページ数は30ページだと言うことが分かりました。
図を使って考えてみました。
意味が分かっている方には無駄な作業に見えるのですが、子どもたちが何をしているのか分からないときには効果的です。
何をしているのか分からないというときには、図から入るのがおすすめです。
「〇の△倍だから式はどうなるの？」と大人が子供に迫るとなんとなく\(〇\times △\)と答えがちです。
一時的にはできているように見えるのですが、実際にはできていないということも少なくありません。
絵図や線分図などでビジュアル化して見えるようにして、お子さんに理解してもらうのがいいのではないでしょうか。
練習問題
1、花だんに白い花と赤い花がさいています。そのうちの3りんは白い花です。赤い花が白い花の4倍さいているとき、赤い花は何りんさいていることになりますか。
2、花子さんの妹の足の大きさは9\(cm\)です。花子さんのお父さんの足の大きさは、花子さんの妹の足の大きさを1とみると3にあたります。花子さんのお父さんの足の大きさは何\(cm\)ですか。
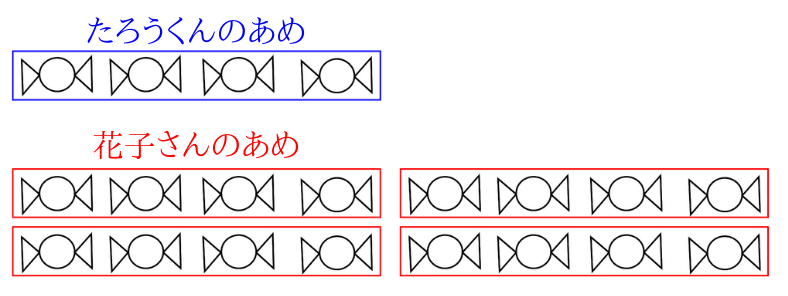
3、たろうくんはあめ玉を4つ持っています。花子さんはたろうくんの4倍のあめ玉を持っています。花子さんが持っているあめ玉は何こですか。
解答と解説
1の解説
白い花が3りんあり、赤い花がその4倍さいているので、\(3\times 4=12\)となり、赤い花は12りんさいていることになります。
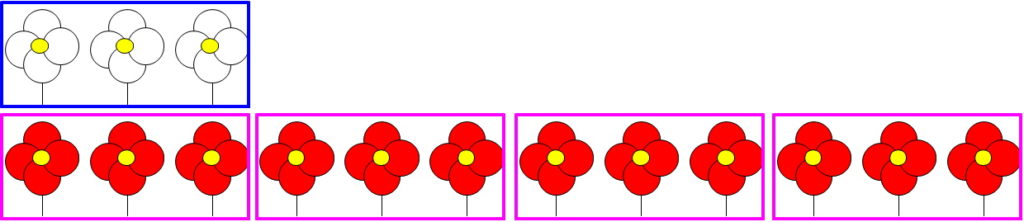
2の解説
花子さんの妹の足の大きさは\(9cm\)で、花子さんのお父さんの足の大きさが花子さんの妹の足の大きさを1とすると3なので、\(9\times 3=27\)となり、花子さんのお父さんの足の大きさは\(27cm\)となります。
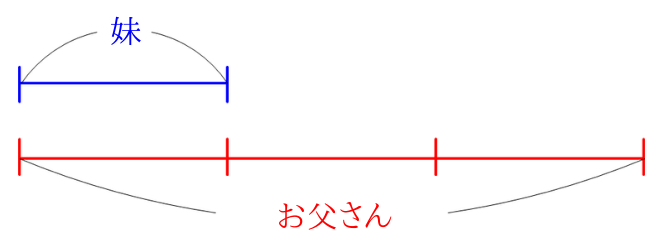
3の解説
たろうくんがあめ玉を4つ持っていて、花子さんはその4倍のあめ玉を持っているので、\(4\times4 =16\)となり、花子さんの持っているあめ玉は16ことなります。
まとめ
今回の記事では何倍かが分かっているときの倍の計算のやり方について書いてみました。
内容的にはそんなに難しくないところだと思います。
しかし、イメージができていない子供たちにとっては割り算なのかなぁ…、掛け算なのかなぁ…と考えてみてもさっぱり分からないということになります。
まずは何をしているのかをしっかりイメージができることが大切です。
文章問題をそのまま絵図や線分図にしているように見えるかもしれませんが、きちんと描くことで何をしているのか理解しやすくなります。
口頭だけで、言葉だけで教えようとすると、どうしても何算かを無理やり言わせることになりがちです。
さらには、お子さんがそのことを理解しているのかの判断がとても難しいのではないでしょうか。
ただ式が立てられる、問題が解けるというのではあとあとの算数や数学ができるのかが心配になってしまいます。
時間はかかってしまいますが、絵図や線分図を使って理解してもらえるのがおすすめですよ。
【関連記事はこちら】
・倍の計算の仕方の教え方は？割り算になる理由って？
