単純に公式に入れればいい面積の問題は覚えてしまえばすんなり解けることがほとんどです。
しかし、困るのが長方形を組み合わせたような面積の問題です。
今回の記事では、面積の応用問題の複合図形の面積の求め方について書いてみたいと思います。
小4で学習する面積の応用問題を解いてみよう
それでは例題を使って面積の応用問題、複合図形の面積の求め方についてみていきましょう。
(角は全て90度とします。)
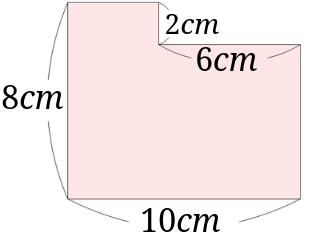
色々な方法でこの例題を解いてみましょう。
2つの長方形に分けて解く方法①
まずは全ての辺の長さを求めましょう。
求めた辺の長さを図に書き込んでみます。
次に図のように2つの長方形に分けます。
そして長方形の面積を1つずつ求めます。
上の長方形の面積は、\(4\times 2=8cm^2\)となります。
それから下の長方形の面積を求めると、\(6\times 10=60cm^2\)
あとは、上と下の長方形の面積を足すと、\(68cm^2\)となります。
2つの長方形に分けて解く方法②
もう1つ、2つの長方形に分けて解く方法をみてみましょう。
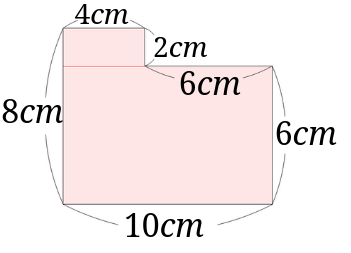
まずは先程と同じように全ての辺の長さを求めて、図に書き込んでいきます。
そして、今度は下の図のように縦に線を入れて2つの長方形に分けます。
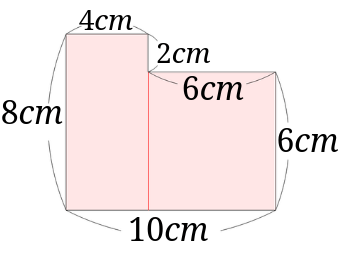
左側の長方形は、\(8\times 4=32cm^2\)
右側の長方形(正方形)は、\(6\times 6=36cm^2\)となります。
後は先ほどの解き方と同じように2つの長方形の面積を足して、\(68cm^2\)となります。
大きな長方形を求めてそこから余分なところを差し引く方法
今度は図の青い線で構成された長方形から青で塗った部分を引いて赤で塗ってある図形の面積を求めてみましょう。
まずは図のように欠けている部分を含んだ面積を求めます。
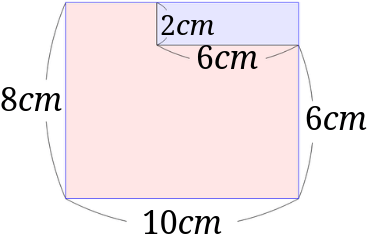
図の部分の長方形は、\(10\times 8=80cm^2\)
次に青で塗った部分の面積を求めて、先ほど求めた長方形の面積から引きます。
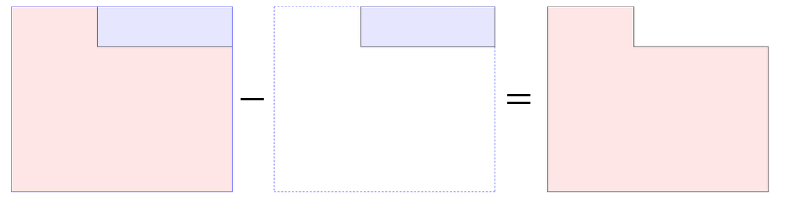
欠けている部分の面積は、\(2\times 6=12cm^2\)
全体から今求めた長方形を差し引いて、\(80-12=68cm^2\)となります。
1つの問題に対して色々な求め方があります。
単に長方形や正方形の面積を求める問題と比べると様々な求め方があり、混乱しやすくなってしまいます。
できるだけ楽な方法で解けるようになるといいですね。
もう1問解いてみましょう。
(角は全て90度とします。)
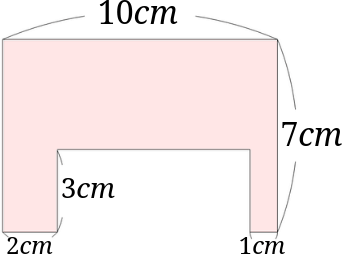
それでは解いてみましょう。
今度の問題も先ほどと同じように解くことができます。
3つの長方形に分けて面積を求める
図のように長方形を分けてみます。
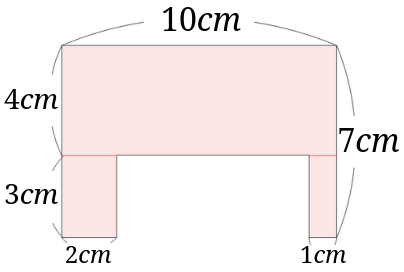
3つの長方形の面積を求めましょう。
上の長方形は、\(4\times 10=40\)
同様に左下の長方形と右下の長方形を求めるとそれぞれ\(6cm^2\)、\(3cm^2\)となります。
あとはこれらを足して、\(40+6+3=49cm^2\)となりました。
大きな長方形から余分なところを差し引く
図の長方形の面積から余分な長方形を引きます。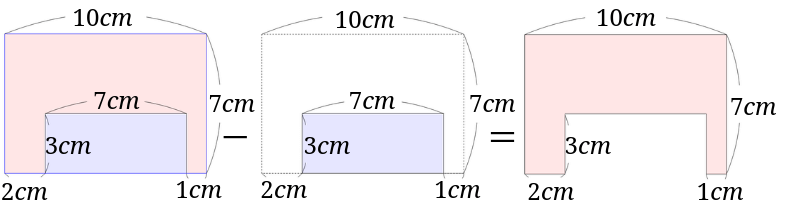
\(10\times 7 – 7\times 3=49cm^2\)
図形の形を変えてみる
図形を切り貼りして、もっと求めやすい形にしてしまうというやり方もあります。
まずは先ほど3つに分けた図からスタートしてみます。
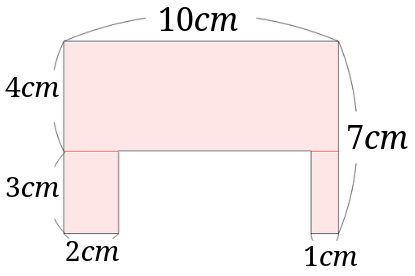
次に左下の長方形を右側にもっていってみましょう。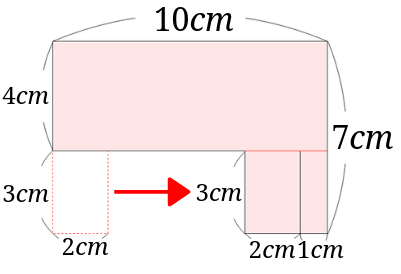
さらに図の部分の縦\(4cm\)、横\(3cm\)の長方形を切り離します。
すると図の部分の欠けている部分と今切り取った長方形は全く同じ形です。
図の欠けている部分に今切り取った長方形をはめてみましょう。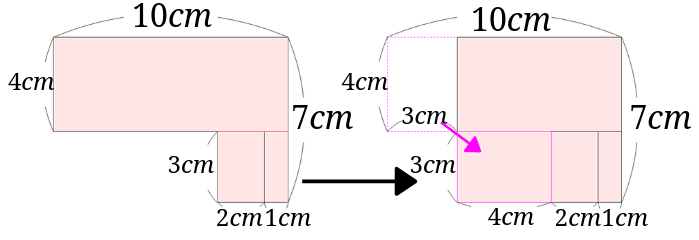
すると1辺が\(7cm\)の正方形が出来あがりました。
この正方形の面積を求めると、\(7\times 7=49cm^2\)となります。
まとめ
今回の記事では、長方形や正方形を組み合わせた複合図形の面積の求め方について説明しました。
長方形や正方形を組み合わせた図形の面積は、複数の長方形に分けてしまう方法や、余分な部分を含んだ面積をまず求めて、それから余分な部分を差し引く方法などがあります。
問題によってはさらに今回紹介したものとは違う方法でも解けることもあります。
複合図形が苦手という場合はまずは知っている形に分けることができると面積を求める第一歩になります。
長方形や正方形を組み合わせた図形だと、長方形や正方形に分けることはさほど難しくはありません。
どうしてもできない場合は、図形を知っている形に分けていってもらいましょう。
それから余分なところを差し引くなどの方法を身に付けていけるといいのではないでしょうか。
例題2でした図形の形を変えてみる方法はこの例題では思いつきにくい解き方ですし、長方形に分割して解くか、大きな図形から余分なところを差し引く方が易しいです。
ここでは、こんなこともできるのかと思ってもらえたらいいと思います。
求める図形の形を変えることは後々役に立ちますよ。
・面積のまとめへ戻る