形が綺麗な立体ではないものや形がいびつなものの体積をはかる方法の1つに、水を使う方法があります。
今回の記事では、水槽に沈めた石の体積の求め方について説明します。
水の入った水槽に石を沈めて体積を求める方法
それでは、早速例題を使って説明していきます。
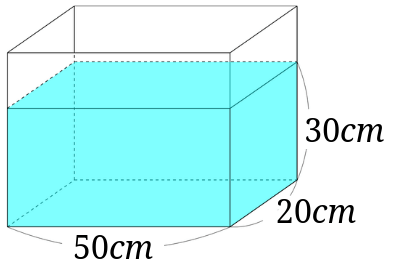
この水そうに石をしずめると、水面が30\(mm\)高くなりました。この石の体積は何\(cm^3\)ですか。
この問題はイメージが湧かない子にはすごく難しい問題になります。
沈めた石の分水位が上がることになります。
下の図のように水位が上がった部分(ピンク色にしている部分)が、石の体積ということになります。

\(20\times 50\times \times 3=3000cm^3\)となります。[1]\(30mm\)を\(3cm\)に単位を変えて計算しています。
この問題の難しいところが、水の水位が上がった分が石の体積ということが理解できるかというところです。
ここが分からないと計算式をいくら教えても何をしているのかの理解ができません。
お子さんが、石を沈めた時に、水位が上がった体積分が石の体積だというイメージが難しいときはお風呂に入った時の水面の上下でイメージしてもらうといいと思います。
それでも理解できない時は、お湯をいっぱいに湯船にためて、お風呂に入ってあふれたお湯の量が自分の体積であることを体験してもらうのもいいかもしれません。
体験すると理解できるようになることが多いです。
もっと手軽な方法だと、バケツなどに水をいっぱいにためて、ある程度体積の大きなもの、例えばりんごなどを沈めてみるという体験をしてもらうのもいいですね。
また、一旦取り出して水位が下がったことを確認したところで、もう一度やってみると水があふれないことを確認すると理解が深まると思います。
石を沈めた状態の体積と元の水の体積の差から石の体積を求める方法
先ほどの計算式は、上がった水面の高さを高さとして計算しました。
石を入れた後の体積から、石を入れる前の体積を引きます。
石を沈めた時の体積は、石の体積と水の体積を合わせたもので、石を沈める前の体積は水のみの体積です。
これら2つの体積の差を取るということは、
石を沈めた時の体積-石を沈める前の体積
=(石の体積+水の体積)-水の体積
=石の体積
となるので、石を入れた後の体積を石を入れる前の体積の差を取ればいいということが分かります。
図で示すと、このようなイメージです。
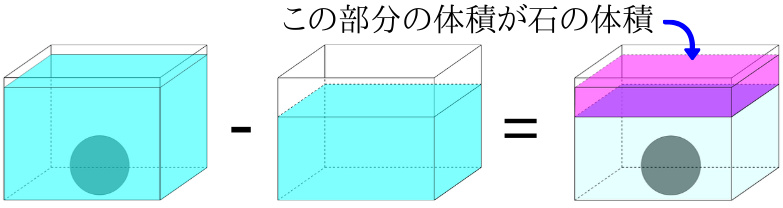
まずは石を入れた後の体積を求めます。
\(20\times 50\times (30+3)=33000cm^3\)[2]\(30mm\)の単位を変換して\(3cm\)で計算しています。
ここから、石を入れる前のもともとの水の体積を求めます。
\(20\times 50\times 30=30000cm^3\)
あとは、石を沈めた時の水と石の体積から、石を沈める前の水の体積を差し引くことで石の体積を求めることができます。
\(33000-30000=3000cm^3\)
となります。
まとめ
今回の記事では、水槽に沈めた石の体積の求め方について説明しました。
お子さんが最初の理解に苦しむことがあるのは、水位が上がった分の水の体積が、石の体積と一致するということです。
この辺りは生活で実感がない場合には理解するのに時間がかかることがあります。
こういうところは、あまり論理的に説明しても想像がつかないと理解してもらうのは難しいです。
手間もかかるので回り道に見えますが、お子さんに実感してもらうのが1番だ思います。
それが分かれば、あとは水位が上がった分の体積を直接求めるか、水位が上がった状態の水と石の体積の和をだし、最初の水のみのときの体積を差し引くことで、石の体積を求めることができます。
扱う対象が水という形がはっきりしないものになると苦手とする子がグッと増えますが、公式的に丸暗記で済ませずに、きちんと理解して解けるといいですね。
お子さんに実感が伴えば、そんなに難しいという問題にはならないと思います。
逆にいうと実感が伴わなければなかなか難しい問題になります。
・かさ・体積・容積のまとめへ戻る