仮分数を帯分数に直すことを苦手としている小学生は結構多いです。
今回の記事は、仮分数を帯分数に直す方法について説明してみたいと思います。
仮分数を帯分数にするときの直し方の教え方は?
それでは早速仮分数を帯分数になおす方法を見ていきましょう。
仮分数を帯分数に直すには、分子を分母で割り、余りまでだします。
そして、商を分数の左横に、余りを分子にするとOKです。
例題を使って、実際にやってみましょう。
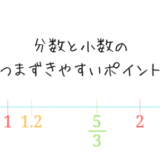
(1)\(\frac{17}{7}\)
(2)\(\frac{26}{10}\)
(1)\frac{17}{7}からみていきます。
分子を分母で割ってみます。
\(17\div 7=2\cdots 3\)
となりました。
このとき商は2、余りは3です。
そのため、仮分数にすると、\(2\frac{3}{7}\)とすることができました。
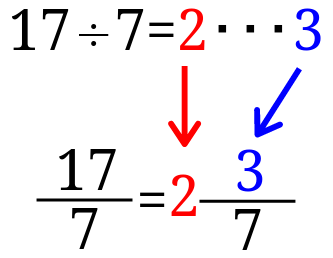
(2)\(\frac{26}{10}\)を帯分数にしていきます。
分数は約分できるときは先に約分をするといいです。
この仮分数の分母と分子が偶数なので、分母と分子を2で約分します。
すると、\(\frac{13}{5}\)になり、先ほどと同じように分子を分母で割ります。
\(13\div 5=2\cdots 3\)となるので、
\(\frac{24}{10}=2\frac{3}{5}\)となります。
なぜこの直し方で仮分数を帯分数にすることができるのか
(1)\(\frac{17}{7}\)を使って説明します。
\(17\div 7=2\cdots 3\)をして、帯分数の整数の部分と分子を決定しました。
この式の意味合いは、17のなかに7の塊が2つでき、3余ったという意味です。
図示するとこんな感じです。

●1つは\(\frac{1}{7}\)なので、●が7つあれば、1ということになります。
つまり赤い四角1つ分が1を示しています。
このときは、●7つの塊が、2つあるので、分数の外に2と書くことになります。
また青い●が3つ余っているので、分数の部分は\(\frac{3}{7}\)ということになります。
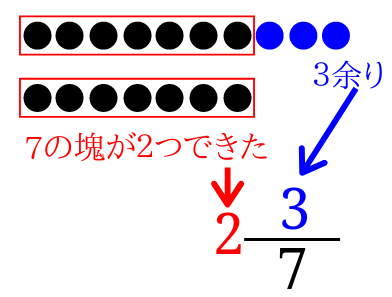
また、このことを式として考えると、
\(\frac{17}{7}\)
\(=\frac{7+7+3}{7}\)
\(=\frac{7}{7}+\frac{7}{7}+\frac{3}{7}\)
\(=1+1+\frac{3}{7}\)
\(=2\frac{3}{7}\)
となります。
仮分数を帯分数に直す問題の教え方のポイントは数直線!
上記の内容でお子さんに説明していってもピンと来ないときには数直線で説明するのも手です。
まずは数直線を書いてください。
整数と整数の間は分母の数に等分した目盛りを入れてください。
(1)\(\frac{17}{7}\)を例に説明します。
この場合は分母が7になっているので、整数と整数の間は7等分にします。
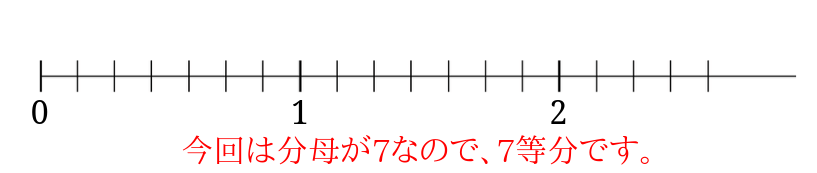
さらに分数の値を目盛りにふっていきます。
数直線の上には仮分数で、数直線の下には帯分数で目盛りに値をふりました。
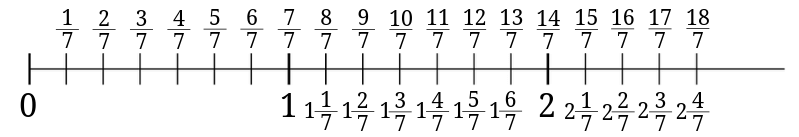
こうしてみてみると、仮分数と帯分数の値の対応関係がよく分かります。
また、分子を分母の塊がいくつあるのかを考える理由も分かりやすくなるのではないでしょうか。
まとめ
今回の記事は、仮分数を帯分数に直す方法について書いてみました。
やり方そのものは難しいということはないのですが、忘れてしまう子はすぐに忘れてしまうので、必要になる度に教えていくことになると思います。
ただ、実際、学年が上がっていくにつれ、仮分数を帯分数にしないといけないということはそんなにありません。
逆の帯分数を仮分数にする場合は結構あります。
そうはいっても、仮分数の整数部分が必要になるということはあります。
このような時は、仮分数を帯分数に直すことが明記されていなくても理屈としては同じことをすることになります。
しっかり理解して、仮分数を帯分数に直すことができるようにしていれば、そんなときでも容易に対処ができると思いますよ。
【関連記事はこちら】
・帯分数は仮分数に直すのは絶対なの?分数をそのまま計算した方がいいときってある?