比例のグラフは書ける子にはそんなに難しいものではないのですが、なかなか飲み込めないというお子さんも一定数見られます。
今回の記事では、そんな比例のグラフがうまく書けない小学生のための比例のグラフの書き方について書いてみたいと思います。
小学6年生で学習する比例のグラフの書き方
比例のグラフの特徴をまずはしっかりおさえることができると、スムーズにグラフを書くことができます。
まずは比例のグラフの特徴を押さえるようにしましょう。
比例のグラフの特徴
比例のグラフは直線
比例のグラフの特徴の1点目は、グラフが直線であるということです。
当たり前のことと思われるかもしれませんが、きちんとお子さんに「比例のグラフは直線である」ということを認識してもらうといいと思います。
グラフが直線であるということが分かれば、2点を定めることで比例のグラフが書けるということが分かります。[1] … Continue reading
比例のグラフは原点を通る
比例のグラフの特徴の2点目は、比例のグラフは必ず原点を通るということです。
つまり、比例であるということが分かれば、1点は自動的に原点に定まるということになります。
1つの直線を書くには、2点が必要ということを書きましたが、このことから、実質的には原点とは異なる点を1つ定めれば比例のグラフを書くことができるということがいえます。
それではこのことをふまえて、例題を使って比例のグラフを書いてみましょう。
\(y=2x\)
\(y=2x\)の\(x\)と\(y\)は比例の関係です。
\(x\)と\(y\)が比例の関係ということは、原点を通ることが分かるので、まずは原点に点を打ちましょう。
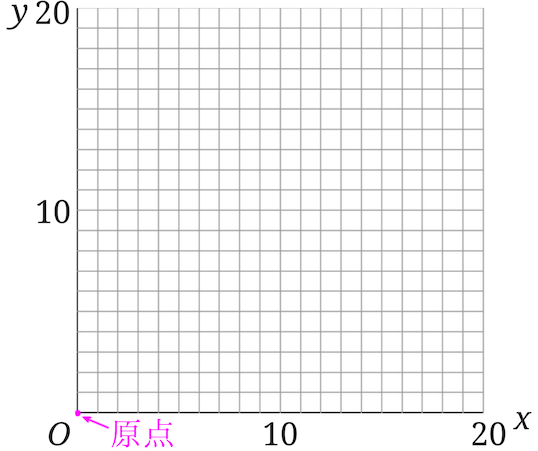
比例のグラフは直線なので、もう1点を定める必要があります。
\(y=2x\)に、\(x=1\)を代入すると、\(y=2\)ということが分かります。
これが2つめの点になります。
\(x\)が1で、\(y\)が2の座標をグラフに書き込みましょう。
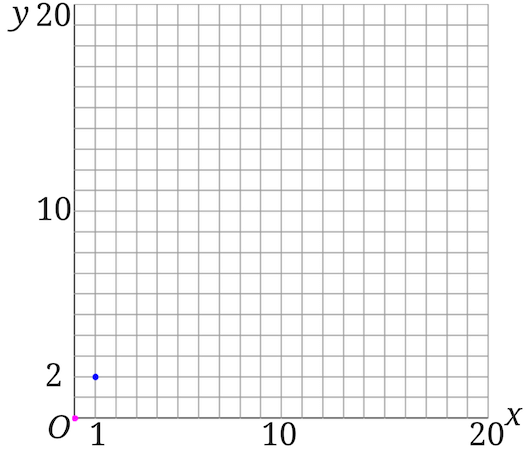
こんな感じで、グラフ上に2つ点ができました。
あとはこの2点を結ぶだけです。
こんな感じです。
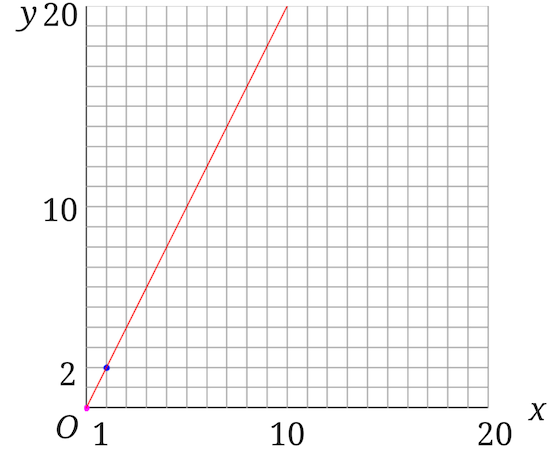
書き方は合っているのに不正解になってしまう比例のグラフとは?
2点を打って結べば比例のグラフが書けるというのは正しいのですが、ちょっと注意して貰いたいこともあります。
それはグラフの正確性です。
小学生が比例のグラフを書くときは、方眼紙のように目盛りが綺麗に打ってあると思います。
これが学年が上がると白紙になっていくのですが、じつはこの目盛りが曲者なんです。
実際点と点を結べばいいという理屈は正しいのですが、その点と点を結んだ直線が、格子点[2] \(x\)座標と\(y\)座標のどちらもが整数の座標のことです。グラフの縦の線と横の線の交わった点だと思って大体大丈夫です。を外してしまうと減点なってしまうことがあります。
下の左のグラフの比例のグラフは正しく書けています。
原点と(1, 2)の座標を取って直線を書く・・・セオリー通りです。
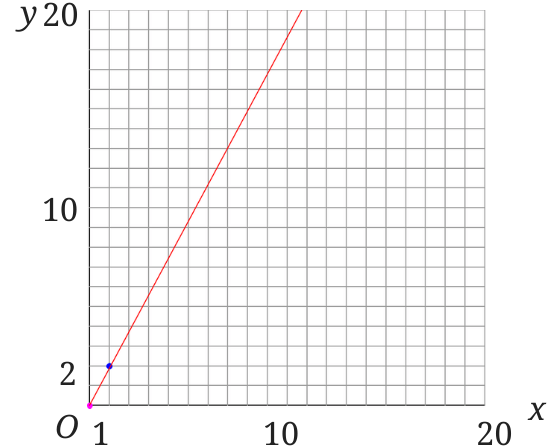
しかし、このグラフは小学校のテストなどでは丸をもらうのは難しいかもしれません。
どこに問題があるのでしょうか。
先程のグラフは2点を打ってその点を結ぶことで正比例のグラフを書きました。
さらに通るべき点を打ってみます。
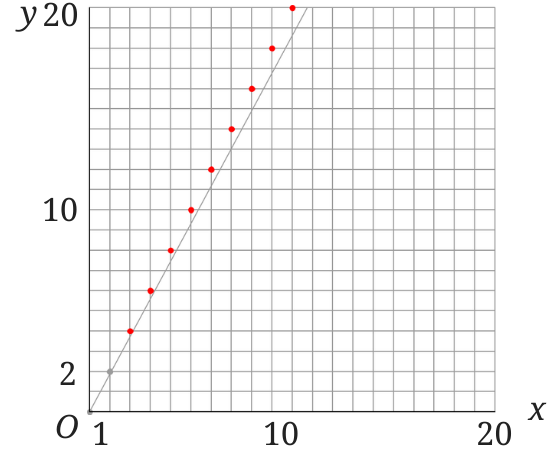
すると通るべき点を随分とはずしていることが分かります。
このように2点を打って結んでも誤差が大きくでてしまうということがあるので、テストなどでは複数点を打つなどしてグラフを書くといいと思います。
このことは減点対象になるから気を付けるというよりは、グラフがどこを通るのかの意識をしっかり身につけるために、きちんと徹底させておくことが大事です。
きちんと通すべき格子点は通して比例のグラフを書けるように教えて上げるといいですね。
比例のグラフを直線できちんと書いても通るべき点を通らないことも・・・
小学校でコピーされたプリントによってはどう頑張っても格子点を通らないこともあります。
印刷の関係で、誤差ができてしまったのかもしれません。
そんなときはそれなりな直線のグラフで提出してしまえばいいと思います。
もしそんなグラフでお子さんがきちんとグラフが書けない!と言い出したら、グラフを書くために打った点以外の点も意識できているのでとてもいい感じだと思います。
比例のグラフが書けないときは
上記のやり方で比例のグラフが書けないときは、一旦表を作ってみましょう。
また、お子さんの比例に対する理解が浅いときに、その理解を深めるという意味で表を書くのはおすすめです。
下のような感じの簡単な表でOKです。
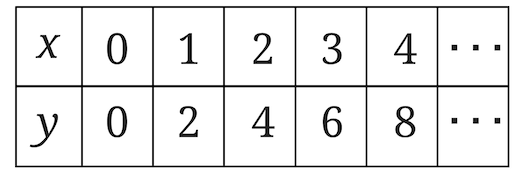
表が書けたら、次は表にした点をグラフに書いていきます。
効率的にするには、2点だけをグラフに書いて、その2点を結ぶべいいのですが、このことにお子さんがピンとこないこともあります。
また、手間を掛けてせっかく表を書いたのですから、表で求めた点を全てグラフに書いてみましょう。
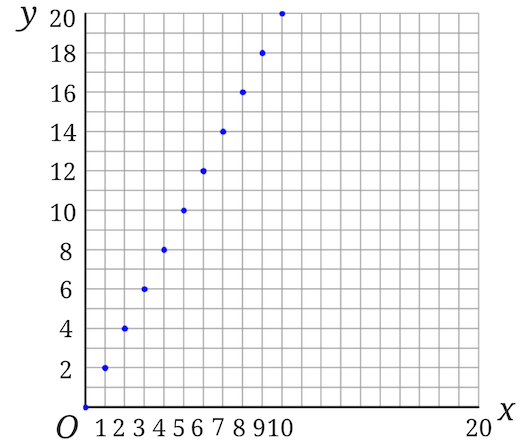
書いているうちに点が一直線になるということに気付けばOKです。
そのことに気付くことができれば、2点をグラフ上にうちその2点を結ぶということに気付くのは時間の問題でしょう。
ただこのときは2点を求めて、比例のグラフを書いていると思います。
このうちの1点を、原点にすれば実際に求める点は1つだけで大丈夫ということに気付けます。
まとめ
今回の記事では、小学生の比例のグラフの書き方について書いてみました。
基本的には、点をきちんとだして、その点をグラフに2つ以上書いて、それらの点を結べばグラフを書くことができます。
このやり方で学校のテストでも十分点を取ることは出来るはずです。
しかし、この比例の単元は中学生や高校生になっても、何度も何度も登場する単元です。
特に関数の基礎としてみれば、より深い理解をお子さんに持って貰うのが後々を考えてもおすすめです。
単に効率的にグラフを書ければ良いという知識で終わらせてしまうのは勿体ないです。
なぜ2点をグラフ上に書くことで比例のグラフを書くことができるのか。
どうすると比例と判断できるのか。
など、考えることは答えを書く以上に色々あります。
なぜこんなことを言うのかというと、比例をきちんと理解していないお子さんはかなり多いのです。
中学でその理解不足があらわになるということもあります。
小学生のうちにきちんと理解して数学の土台をしっかり作ってあげたいところです。
▼関連記事▼
・小学校で習う算数の比例の意味はこちら




