「分数×分数」の掛け算であれば、分母同士分子同士を掛け合わせればいいので、すんなりできるようになるお子さんが多いものです。
しかし、これが「整数×分数」の計算となると、つまずくお子さんが意外と多くなります。
その原因は、整数が1段しかないのに対して、分数が2段あることです。
いざ計算しようとしてみると、整数は分数の上に掛けたら良いのかなぁ?、それとも分数の下に掛けたらいいのかなぁ?とよく分からなくなってしまうお子さんもおられます。
今回の記事では、約分がある「整数×分数」の計算の仕方について書いてみたいと思います。
整数と分数の約分ありの掛け算の解き方
それでは早速例題をみていきましょう。
$$(1)4\times \frac{3}{7} (2)8\times \frac{5}{12}$$
$$(1)4\times \frac{3}{7}$$からみていきましょう。
約分なしの計算問題を入れてみました。
まずはこれができなければ進めません。
そのまま計算する
「整数×分数」の計算は整数と分子を掛けることで計算することができます。
そのまま計算して、
\(4\times \frac{3}{7}=\frac{12}{7}\)という感じでOKです。
整数を分数にして計算する
4を\(\frac{4}{1}\)にしてから計算してみます。
\(4\times \frac{3}{7}=\frac{4}{1}\times \frac{3}{7}=\frac{4\times 3}{1\times7}=\frac{12}{7}\)という風になります。
整数を分数に直すことで、「整数×分数」を「分数×分数」の計算と同じように解くことができるようになります。
「整数×分数」がどうしてもうまくいかない!という時にはおすすめの方法です。
慣れてきたら整数を分数に変えることなくそのまま計算できるようにするとばっちりです。
・約分がない整数と分数の掛け算からできないときは?
約分なしの計算ができたら次の問題に移ります。
$$(2)8\times \frac{5}{12}$$の計算をしてみましょう。
この場合も先程の(1)の約分のない「整数×分数」の計算の時とやり方そのものは同じです。
基本は整数と分子を掛けることで計算をすることが可能です。
それではまずはそのまま計算してみましょう。
そのまま計算する
整数と分子を掛けるので、この時「整数」と「分母」の両方が同じ数で割れるときに約分をすることが可能になります。
(2)の場合であれば、整数の8と分数の分母の12のどちらも、4で割ることができます。
整数と分子を掛け合わせる前に約分をして、
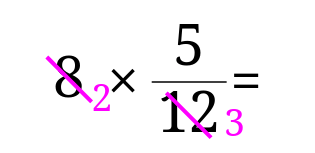
約分ができたら、(1)の時と同じように整数と分子を掛けたらできあがりです。
この問題の答えは\(\frac{10}{3}\)となります。
整数と分母をどうしても上手く約分することができないときは、整数を分数に変えて計算するとやりやすくなります。
整数を分数に直して計算する
整数の8を\(\frac{8}{1}\)にして計算をしてみましょう。
すると、「分数×分数」の場合と同じように約分・計算をすることができるようになります。
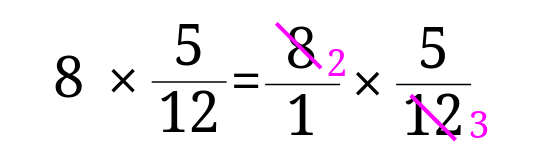
「分数×分数」にすることで、随分と計算がしやすくなると思います。
「分数×分数」の計算は学校でもかなりの量の計算をしていることが多いです。
そのため「整数×分数」の計算式の整数を分数に直して「分数×分数」の計算式にしてしまうとお子さんにとってはやりやすい、見慣れた計算となります。
どうしても「整数×分数」の整数を分母に掛けてしまったり、混乱して計算ができなかったりする場合は、まずは整数を分数にして、見慣れた「分数×分数」の計算にするとスムーズに勉強を進めることができますよ。
慣れてきたら、整数を分数に直すことなく計算ができるようにしておいた方が後々計算が楽になります。
どうしてもそのまま計算することが無理!という時は、そのまま整数を分数に直して計算し続けても計算のスピードくらいで大きな問題になることは少ないと思います。
ただ途中で約分ができない!というのは、計算したときの数字が大きくなりがちになってしまうので、計算の途中で約分できるようにしておきましょう。
数字が大きくなることで計算ミスが増えたり、数字があまりに大きくなってしまうと約数が見つけられない・・・なんてことになってしまうこともあります。
練習問題
1、\(4\times \frac{5}{6}\)
2、\(\frac{3}{14}\times 21\)
3、\(\frac{11}{8}\times 6\)
4、\(10\times \frac{4}{15}\)
5、\(12 \times \frac{7}{16}\)
解答
1、\(\frac{10}{3}\)
2、\(\frac{9}{2}\)
3、\(\frac{33}{4}\)
4、\(\frac{8}{3}\)
5、\(\frac{21}{4}\)
まとめ
今回の記事では、約分がある「整数×分数」の計算について書いてみました。
大人目線では、分数同士の計算よりも易しく見えてしまうので、なぜ解けないのかなぁ?と思ってしまうこともあるのではないでしょうか。
しかし、お子さんは、基本的に「分数×分数」の計算には慣れているので、見慣れた計算にうまくもっていくことで安定して解けるようになるお子さんも少なくありません。
もちろん、こんなことしなくてもそのまま計算できるということであれば、そのまま計算をする形で問題ないと思います。
・分数のかけ算の約分ができない!なぜ斜めでできるの?意味の教え方やコツはどう説明する?




