分数のかけ算の約分ができない！なぜ斜めでできるの？意味の教え方やコツはどう説明する？

分数の掛け算は分数の計算のなかでもやりやすい計算です。

特に前回したような約分をする必要がない分数の掛け算は計算しやすいと思います。

しかし、ここに約分という考え方が加わってくると今までの約分のない分数の掛け算とは違ってきます。

今回の記事では、約分のある分数の掛け算の計算について書いてみたいと思います。

分数のかけ算で約分ができない子への教え方とそのコツ

今回は約分のある分数の掛け算を扱っていきます。
それでは早速例題を元に説明していきますね。

例題

次の計算をしてしましょう。
$$(1)\frac{3}{8}\times \frac{2}{5}　(2)\frac{5}{6}\times \frac{3}{10}$$

(1)からみていきましょう。

(1)$\frac{3}{8}\times \frac{2}{5}$

約分が計算の途中で出来るようになろう！

この計算は途中で約分することができるので、計算の途中で約分してしまうのが望ましいです。
算数が苦手なお子さんの中には、途中で約分するのが難しいということで、いったん計算してしまって、最後に約分をしようとしてしまう子がいます。

(1)をこのやり方で解いてみると、

$\frac{3}{8}\times \frac{2}{5}=\frac{3\times 2}{8\times 5}=\frac{6}{40}=\frac{3}{20}$

といった感じになります。
もちろんこれでも正解です。

途中で約分ができないということは、一旦分子と分母の数字が大きくなってしまうことを意味します。
ということは、計算して、約分して答えという手順を踏むことになります。
計算してから約分できる数字を探すときに、途中で約分しないと数字が大きくなってしまい、約分できる数字があるのかどうかが分からないということになってしまう子もいます。
そうならないためにも、きちんと手順通りに、計算途中で約分をすることができるようにしましょう。

途中で約分をして、(1)を解いてみましょう。

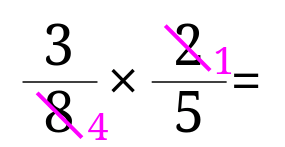
分数の掛け算では斜めの数字同士で約分してから計算すると楽ちんです。
きちんとできるようにマスターしましょう。
約分が済んだら続きを計算するだけです。
計算すると(1)の答えは、$\frac{3}{20}$となります。

なぜ、約分できるの？

なんとなく約分って「斜めの数字が同じ数字で割れるときは割っていい」という感じに見えますが、なぜ約分をすることができるのでしょうか。
少し数式をいじってみましょう。
例題の(1)を使って考えてみましょう。

$\frac{3}{8}\times \frac{2}{5}=\frac{3\times 2}{8\times 5}$

ここで分母の計算の順番を入れ替えてみます。

$\frac{3\times 2}{8\times 5}=\frac{3\times 2}{5\times 8}$

さらに分母の8を$2\times 2\times 2$にします。^[1]8を2\times 2\times 2にすることを素因数分解と言います。この場合だと$4\times 2$でも説明することができます。

$\frac{3\times 2}{5\times 8}=\frac{3\times 2}{5\times 2\times 2\times 2}$

さらに式を変形してみます。

$\frac{3\times 2}{5\times 2\times 2\times 2}=\frac{3}{5\times 2\times 2}\times \frac{2}{2}$

$\frac{2}{2}$は1なので、

$\frac{3}{5\times 2\times 2}=\frac{3}{20}$

となります。
分子と分母の数字を同じ数字で割るということは、分母と分子が同じ数の分数を作って消していくという感じになりますね。

それでは(2)をみていきましょう。

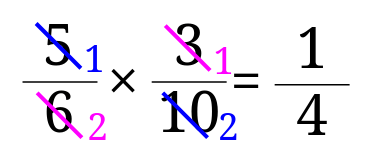
よって答えは、$\frac{1}{4}$となります。

途中できちんと約分ができると数が大きくならないので計算しやすくなります。
きちんと途中で約分できるようにしましょう。
あとから、約分すればいいと考えて、実際に計算した後に約分をする子がいますが、早めに、計算の途中で約分することを覚えさせましょう。
のちのち計算を強制するのは大変なので、早めにできるようにするのがおススメですよ。

練習問題

1、$\frac{7}{9}\times \frac{3}{4}$

2、$\frac{6}{7}\times \frac{5}{2}$

3、$\frac{3}{8}\times \frac{4}{9}$

4、$\frac{4}{5}\times \frac{15}{4}$

5、$\frac{6}{7}\times \frac{14}{15}$

解答と解説

きちんと計算途中で約分をするようにしましょう。

1の解説

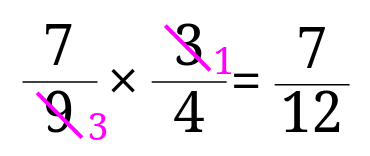答えは、$\frac{7}{12}$となります。

2の解説

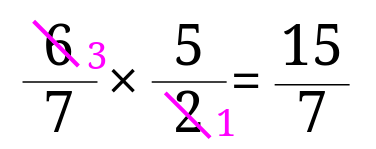答えは、$\frac{15}{7}$となります。

3の解説

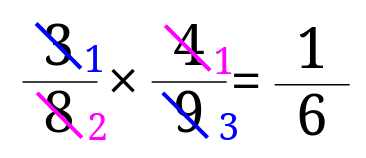答えは、$\frac{1}{6}$となります。

4の解説

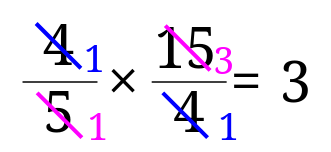答えは、$3$となります。

5の解説

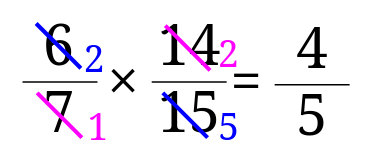答えは、$\frac{4}{5}$となります。

これくらいの問題であれば、途中で約分をしなくてもなんてことなく問題は解くことができます。
そのため、お子さんの中には途中で約分をしないという子も見かけます。
勿論それでも答えには行きつくことができますが、後々分数の計算が苦手！となることが多いのでお子さんがめんどくさがっても早いうちに計算途中に約分できるようにしておきましょう。