通分と約分の違いって何？なぜ分母と分子に同じ数を掛けたり割ったりできるの？

分数の計算でよく登場するのが通分と約分。

同じようなことをしている感じがしますが、何が違うのでしょうか。

今回の記事では、通分と約分の違いについて書いてみたいと思います。

約分って何？

約分をするとはどういうことなのでしょうか。

約分をするというのは、分数の分母と分子を公約数で割ることを意味します。
例えば、\(\frac{4}{12}\)を約分することを考えてみましょう。
4と12の公約数は2と4です。^[1]厳密には1も公約数ですが、約分をする際に1で割るということはないので、公約数から1を除外しています。
この時、約分するということは、分母や分子を2や4で割ることを意味します。
4で割ってみると、\(\frac{4}{12}=\frac{4\div 4}{12\div 4}=\frac{1}{3}\)となります。
2で割ってみると、\(\frac{4}{12}=\frac{4\div 2}{12\div 2}=\frac{2}{6}\)となります。

ただ実際にはこんな式を書くといういことはなく、こんな感じで約分します。

4で割った場合

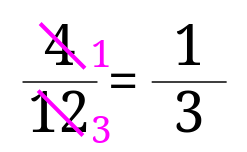
2で割った場合

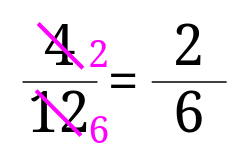
基本的には、分母と分子を公約数で割れば約分といって大丈夫だと思います。

また、「約分する」と言う場合は、分数の掛け算や割り算の計算でもでてきます。

例えばこんな場合です。$$\frac{2}{3}\times \frac{7}{4}$$
分母と分子は同じ数で割っても良いので、$$\frac{2}{3}\times \frac{7}{4}=\frac{2\times 7}{3\times 4}=\frac{2\times 7\div 2}{3\times 4\div2}=\frac{7}{6}$$となります。
この分数の計算も実際にそんな風に書くことはあまり見かけないと思います。
実際には、この分数の掛け算を約分するとこんな感じになります。

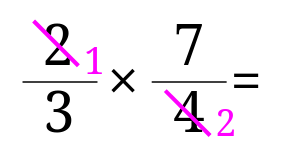
\(\frac{2}{4}\)のような分数を約分する場合と分数のかけ算や割り算の計算のときの約分を例としてみると約分が何をすることなのかというのは分かりやすいと思います。

通分って何？

約分がどんなものなのかをみてきました。
それでは似たような言葉の通分とはどういうことをいうのでしょうか。

通分はとは、いくつかの分数があるときにそれらの分数の分母をそろえることをいいます。
例えば、\(\frac{1}{3}\)と\(\frac{3}{4}\)という分数があるとします。
この時前者の分数の分母は3、後者の分数の分母は4です。
これらの分数の分母をそろえてみましょう。
3と4の最小公倍数は12なので、これら2つの分数の分母を12で揃えてみましょう。
前者の分数の分母と分子に4を、後者の分数の分母と分子に3を掛けてみます。
すると前者の分数は、\(\frac{1}{3}=\frac{1\times 4}{3\times 4}=\frac{4}{12}\)となります。
後者の分数は、\(\frac{3}{4}=\frac{3\times 3}{4\times 3}=\frac{9}{12}\)となり、これで2つの分数の分母をそろえることができました。

このようにいくつかの分数があるときに同じ分母の分数にすることを通分といいます。
分母が異なった分数の足し算や引き算でするイメージが強いと思います。

それでは、なぜ分母と分子に同じ数を掛けてもいいのでしょうか。

なぜ分母と分子に同じ数を掛けていいの？

これは、意外と簡単な理屈です。
どんな数にかけても数が変わらない数が1つありますよね。
1です。

例えば、3に1を掛けても、3は3のままです。
他の数に1を掛けても、数は変わりません。
通分は同じ数を分数の分子と分母にかけるので、結局は1を掛けていることになります。
そのため、元の分数と分母と分子に同じ数を掛けて出た数ともとの分数は、同じものということになります。

まとめ

今回の記事では約分と通分の違いについて書いてみました。

約分をするというのは、分数の分母と分子を公約数で割ることを意味します。
通分はいくつかの分数があるときに、それらの分数の分母をそろえることをいいます。
どちらも基本的にはしていることは同じです。

しかしちょっと注意したいこともあります。
通分は分母の異なった分数の足し算や引き算を解いているうちに、自然と身につきます。
ただ、分数の掛け算や割り算の途中で使う約分の仕方はきちんと意識して使わないと身に付きません。
別に約分をしなくても、いったん計算したあとに約分をすれば、一応は答えにいきついてしまいます。
小学校の段階では必要性が薄く感じるかもしれませんが、後々は計算の途中できちんとできないことで計算がややこしくなりミスや間違いが増えることになります。
計算の途中の約分は使おうと思わないとなかなか身につかないので、約分ができるときは計算の途中で約分をするのがおすすめですよ。

【関連記事はこちら】
・約分が苦手で分数の計算が分からない！分かりやすく意味や理由、コツを理解させる教え方のポイントとは？