約分が苦手で分数の計算が分からない！分かりやすく意味や理由、コツを理解させる教え方のポイントとは？

分数を扱うためには避けて通れないのが約分。

約分をすらすらできると分数の計算をするのもかなり楽になります。

今回の記事では分数の約分の仕方やそのコツについて書いてみたいと思います。

▼他にも見ておきたい小数･分数のつまずきポイントについて▼
分数や小数の単元で小学生がつまずきやすい主なポイントとは？

分数の約分のやり方とは

約分の仕方や意味を端的に言ってしまうと、分子と分母を同じ整数で割ることです。
このときに分母も分子も割り切れる数で割るということがポイントです。

例題を解きながら、約分のやり方をみていきましょう。

例題

次の分数を約分しましょう。
$$(1)\frac{2}{4}　(2)\frac{3}{9}　(3)\frac{4}{12}　(4)\frac{12}{6}$$

(1)からみていきましょう。
約分は分母と分子のどちらも割り切れる数で割るのがルールです。
(1)$\frac{2}{4}$の分子は$2$、分母は$4$なのでどちらも割ることができる数は$2$です。
分子と分母のどちらも$2$で割ると、$$\frac{2\div 2}{4\div 2}=\frac{1}{2}$$となるので、答えは$\frac{1}{2}$となります。
実際には下のような書き方をする方が多いと思います。

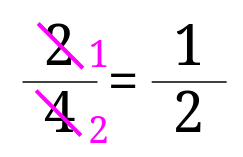
たまに$1$でも割れると豪語する小学生がいますが、割っても問題無いはないけれど、残念なことに数字は変化しません。

次に(2)をみてみましょう。
(2)$\frac{3}{9}$の分子は$3$、分母は$9$なので、とちらも割ることができる数は$3$です。
分子と分母のどちらも$3$で割ると、$$\frac{3\div 3}{9\div 3}=\frac{1}{3}$$となるので、答えは$\frac{1}{3}$となります。

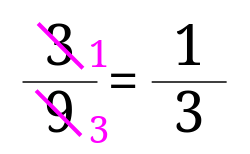
次に(3)$\frac{4}{12}$をみてみましょう。

分数の分子と分母は最大公約数で割るべきなの？

$\frac{4}{12}$の分子は$4$、分母は$12$なので、どちらも割ることできる数は$2$と$4$です。
スマートに約分するには最大公約数で割った方がいいですね。
まずは$4$で割るやり方をみていきましょう。
分子と分母のどちらも$4$で割ると、$$\frac{4}{12}=\frac{4\div 4}{12\div 4}=\frac{1}{3}$$となるので、答えは$\frac{1}{3}$となります。
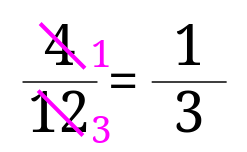公約数で割ってみると･･･

次に(3)$\frac{4}{12}$を$2$で割って約分してみます。
分母と分子を$2$で割ってみると、$$\frac{4}{12}=\frac{4\div 2}{12\div 2}=\frac{2}{6}$$となるので、答えは$\frac{2}{6}$としてしまいがちです。

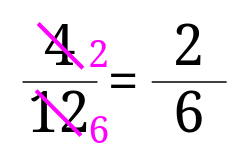
これ以上分母と分子を同じ数で割ることができないところまで約分しないといけないと思ってもらいましょう。
なるべく簡単な整数の分母と分子にして、約分完了！という感じです。
いつも上手く最大公約数で割ることができると言うわけではないので、きちんとこれ以上は分母も分子も割れない！というところまで約分するという意識をお子さんに持ってもらえるようにするといいと思います。
先程の$\frac{2}{6}$は、分母も分子もまだ$2$で割ることができるので、$$\frac{2}{6}=\frac{2\div2}{6\div 2}=\frac{1}{3}$$となるので、答えは$\frac{1}{3}$となります。

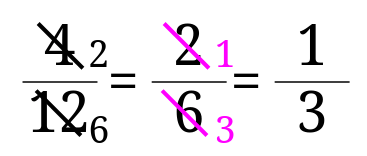
分数の分母が消える場合

次に分母が消える約分をみていきましょう。
(4)$\frac{12}{6}$を約分していきます。
今回は最大公約数の$6$で分母と分子を割ると、$$\frac{12\div 6}{6\div 6}=\frac{2}{1}$$となるので、答えは$\frac{2}{1}$となりそうですが、答えに$\frac{2}{1}$と書いてはダメです。
この時は分母がなくなって、答えは$2$と書くのが正解です。
分母と分子を同じ正の整数で割れば良いとだけ考えていると、答えに$\frac{2}{1}$と書いてしまうので注意が必要です。

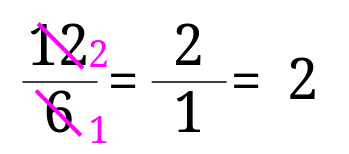
分母が$1$のときは分母を消して、整数で答えるようにしましょう。

練習問題

1、$\frac{2}{8}$

2、$\frac{6}{3}$

3、$\frac{6}{9}$

4、$\frac{5}{10}$

5、$\frac{125}{100}$

6、$\frac{9}{18}$

解答と解説

1の解説

分母と分子を$2$で割って、$$\frac{2}{8}=\frac{2\div 2}{8\div 2}=\frac{1}{4}$$

2の解説

分子と分母を$3$で割って、$$\frac{6}{3}=\frac{6\div 3}{3\div 3}=2$$

3の解説

分子と分母を$3$で割って、$$\frac{6}{9}=\frac{6\div 3}{9\div 3}=\frac{2}{3}$$

4の解説

分子と分母を$5$で割って、$$\frac{5}{10}=\frac{5\div 5}{10\div 5}=\frac{1}{2}$$

5の解説

分子と分母を$25$で割って、$$\frac{125}{100}=\frac{125\div 25}{100\div 25}=\frac{5}{4}$$

6の解説

分子と分母を$9$で割って、$$\frac{9}{18}=\frac{9\div 9}{18\div 9}=\frac{1}{2}$$

まとめ

今回の記事では分数の約分の仕方について書いてみました。
約分は、分子と分母を同じ整数で割ってなるべく簡単な分数にすることだと考えてOKだと思います。
基本的には最大公約数で分子と分母を割ってしまえば、最も簡単な分数にすることができます。

しかし、うまく最大公約数が見つからない時は、単なる公約数で分子と分母を割ってもOKです。
ただし、公約数で割るときは、1度約分ができたからといってそこで約分することをやめないように気を付けましょう。
約分の目的は、なるべく簡単な分数にすることです。
これ以上同じ数字で割れない！というところまで、きちんと約分することが大事ですよ。

・分数や小数のまとめへ戻る