比例の関係の理解ができたら、反比例の関係も分かるようにしておきましょう。
今回の記事では反比例の見分け方について書いてみたいと思います。
小学生にもできる反比例の見分け方
反比例かどうかを見分けるためには、反比例の性質を押さえておくことが大切です。
反比例かどうかを見分けるためには大きく2つの性質を使います。
・2つの量がある時に、片一方の量を2倍3倍…としたときに、もう一方の量が\(\frac{1}{2}\)倍\(\frac{1}{3}\)倍…となる
・2つの量を掛けると、いつも決まった数になる
まずはこれらの2つの意味をしっかり覚えてもらいましょう。
この基本的な性質を使って反比例かどうかを見分けたいと思います。
それでは例題を使って考えてみましょう。
この長方形のたての長さを\(xcm\)横の長さを\(ycm\)とします。
\(x\)と\(y\)がどのような関係にあるのかを考えましょう。
対応表を使って反比例か見分ける方法
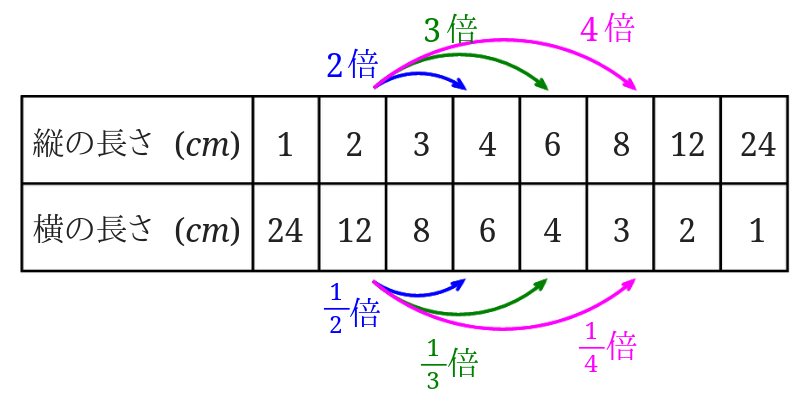
\(x\)と\(y\)の関係を表にして反比例かどうか見分けてみます。
対応表を書いてみると、
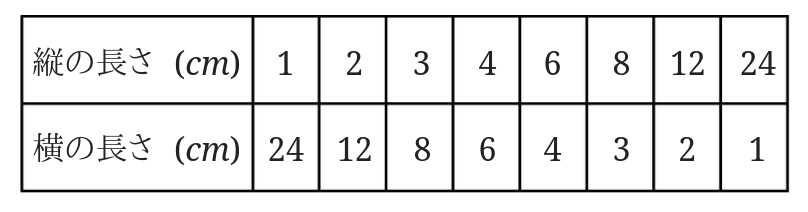
このようになります。
表が書けたら、2つの量がある時に、片一方の量を2倍3倍…としたときに、もう一方の量が\(\frac{1}{2}\)倍\(\frac{1}{3}\)倍…となっているかを確かめてみます。
たての長さが\(1cm\)のところを基準に2倍、3倍…となっているところをみます。
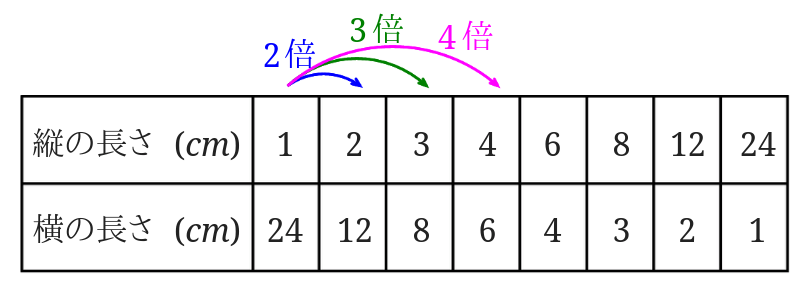 2倍3倍…に対応する横の長さのところを見てみると、\(\frac{1}{2}\)倍\(\frac{1}{3}\)倍…となっていることが分かります。
2倍3倍…に対応する横の長さのところを見てみると、\(\frac{1}{2}\)倍\(\frac{1}{3}\)倍…となっていることが分かります。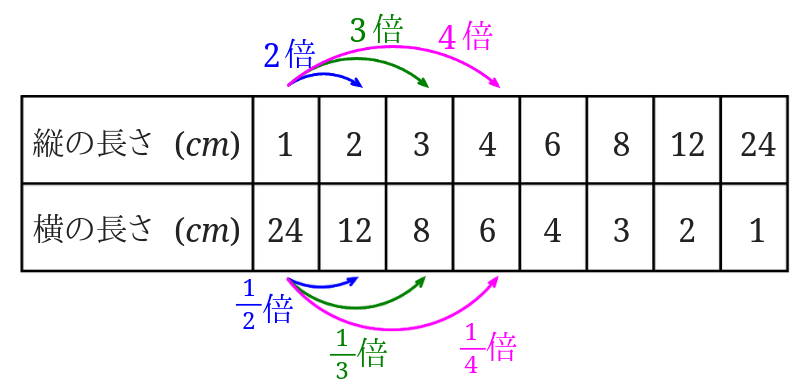 このことから、面積が\(24cm^2\)の長方形のたての長さと横の長さは反比例の関係にあると言えます。
このことから、面積が\(24cm^2\)の長方形のたての長さと横の長さは反比例の関係にあると言えます。
反比例かを見分けるのに\(x\)の値が1のところを基準にみることが多いと思いますが、別にこれはどこをもとにしてもOKです。
次に\(x\)の値、縦の長さが2のところを基準にみてみましょう。
2を2倍3倍…とすると、4、6、8となります。
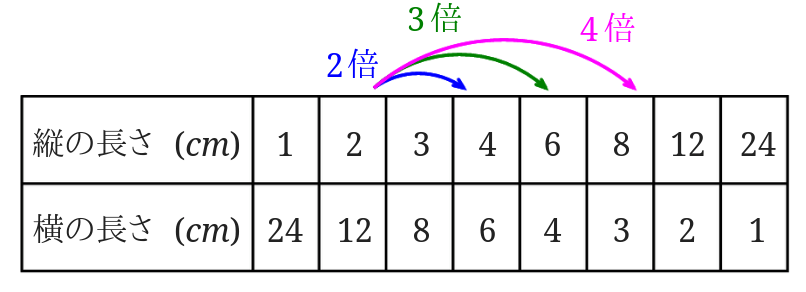 対応する\(y\)の値をみてみると、\(\frac{1}{2}\)倍\(\frac{1}{3}\)倍…となっているので\(x\)と\(y\)、面積が\(24cm^2\)の長方形のたての長さと横の長さはやはり反比例の関係にあるといえます。
対応する\(y\)の値をみてみると、\(\frac{1}{2}\)倍\(\frac{1}{3}\)倍…となっているので\(x\)と\(y\)、面積が\(24cm^2\)の長方形のたての長さと横の長さはやはり反比例の関係にあるといえます。
2つの量を掛けると、いつも決まった数になることを利用して反比例か見分ける方法
次に2つの量を掛けると、いつも決まった数になることを利用して反比例かどうか見分けてみましょう。
たての長さと横の長さを掛けてみましょう。
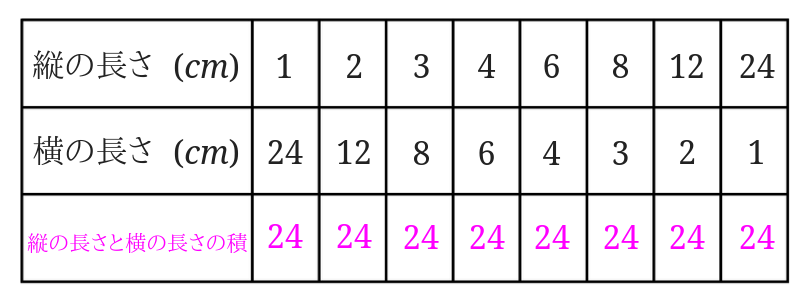
掛けてみると、全て24になりました。
2つの量を掛けると同じ数になることが分かったので、たての長さと横の長さは反比例の関係にあるということが分かります。
この問題の場合だと、こちらの方法が分かりやすいと思います。
そもそも面積が\(24cm^2\)の長方形の縦の長さと横の長さを掛けると、\(24cm^2\)になるはずですよね。[1]縦の長さ×横の長さ=24になります。
そう考えることができれば、対応表を書くよりも縦の長さと横の長さを掛けると決まった数になるという見方の方が楽かもしれませんね。
まとめ
今回の記事では反比例の見分け方について書いてみました。
まず理解して覚えてもらうことは、
・2つの量がある時に、片一方の量を2倍3倍…としたときに、もう一方の量が\(\frac{1}{2}\)倍\(\frac{1}{3}\)倍…となる
・2つの量を掛けると、いつも決まった数になる
この2点が大切です。
文言をきれいに覚えるというよりもきちんと理解して使えるようにしておくといいと思います。
あまり文言にこだわりすぎても役に立たないので、実際にやってみながら理解してもらいましょう。
▼関連記事▼
・小学生にも分かる反比例の意味とは?
References
| ↑1 | 縦の長さ×横の長さ=24になります。 |
|---|




